ГЕОМЕТРИЯЫСЬ ЗАДАЧАЯС СБОРНИК

1 §. Веськыд визь.

Вундӧгъясӧс мурталӧм да на вылын действийӧяс.

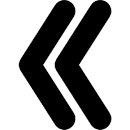
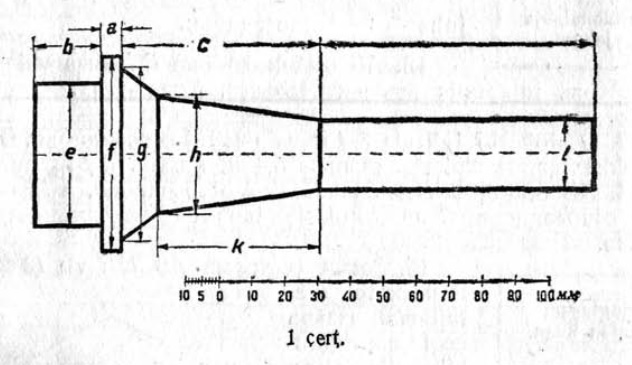
1. 1 чертёж вылын сетӧма станоклысь юкӧн. Сетӧм масштабӧн пӧльзуйтчӧмӧн мерайтӧй чертёж вылын размернӧй визьясӧн индӧм вундӧгъяссӧ да гижалӧй лоӧм лыдъяссӧ тетрадяныд.

2. Йитӧма помся 3 пу балкаӧс, кузьтаясыс налӧн: первойлӧн 4,8 м, мӧдлӧн — 3,4 м, коймӧдлӧн — 5,8 м. 1 см кузя вундӧгӧн 1 м пасйӧмӧн корсьны налысь ӧтувъя кузьтасӧ.

3. Коз пулӧн кузьтаыс вӧлі 20,25 м. Сыысь увсяньыс пилитісны 3,75 м кузя вундӧг («лапа»), а сэсся 7,40 м кузя кер. Кутшӧм кузьтаа лои коз пулӧн кольӧм юкӧныс? (Решитны арифметическӧя да геометрическӧя).

4. 20 м кузя AB вундӧг вылӧ A помсяньыс пуктӧма юкӧн AC = 5,1 м, а B помсяньыс юкӧн BD = 7,9 м. Тӧдмавны CD вундӧглысь кузьтасӧ.

5. Решитны 4-ӧд задача лыдъяссӧ тадз вежӧмӧн: AB = 4,8 м, AC = 2,8 м, BD = 3 м.

6. Чертитны 3a + 2b ыджда вундӧг, кӧн a да b — сетӧм вундӧгъяслӧн кузьтаясыс.

7. Чертитны 4m − 3n ыджда вундӧг, кӧн m да n — сетӧм вундӧгъяслӧн кузьтаясыс (m > n).

8. M чутсянь ӧти веськыд визьӧд да ӧтарлань пуктӧма 2 вундӧг: MN = 100 см да MP = 160 см. Корсьны тайӧ вундӧгъяс шӧръяскостса расстоянньӧсӧ.

9. AB вундӧгӧс юкӧма 2 неӧтыджда юкӧн вылӧ. Тайӧ вундӧгъяс шӧръяскостса расстоянньӧыс 2,75 м ыджда. Корсьны AB-лысь кузьтасӧ.

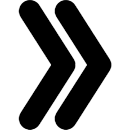
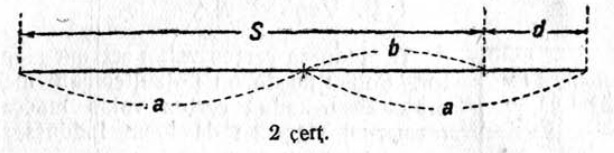
10. Серпас серти (2 чертёж) объяснитны, кыдзи корсьны построенньӧӧн кыкнан вундӧгсӧ, кор налысь сетӧма суммасӧ S да разносьтсӧ d.

Вундӧгъяс вылӧ пропорциональнӧй юкӧм применитӧм.

11. AB вундӧг 2,8 м ыджда. Вундӧг вылын босьтӧма чут, коді сійӧс юкӧ 2⁄3 : 4⁄15 отношенньӧын. Корсьны вундӧг шӧрсянь тайӧ чутӧдз расстоянньӧсӧ.

12. AB вундӧгӧс нюжӧдӧма BC кузьта вылӧ сідз, мый AC AB-ысь m пӧв ыджыдджык. Корсьны AB : BC отношенньӧ.

13. AB вундӧгӧс юкӧма 3 юкӧнӧ 2 : 3 : 4 отношенньӧын. Дорса юкӧнъясса шӧръяскостса расстоянньӧыс 5,4 м ыджда. Определитны AB-лысь кузьтасӧ.

14. AB вундӧг C чутӧн юксьӧ 5 : 7 отношенньӧын, D чутӧн — 5 : 11 отношенньӧын; C да D костса расстоянньӧ 10 м ыджда. Корсьны AB-лысь кузьтасӧ.

Чегласьӧм визьлӧн кузьтаыс.

15. Сетӧма ABCDE чегласьӧм (3 чертёж). Муртавны быд вундӧг да корсьны налысь суммасӧ. Построенньӧӧн веськӧдны чегласьӧм визьсӧ да муртавны артман вундӧглысь кузьтасӧ. Сравнитны кыкнан артмӧм ӧтветсӧ.

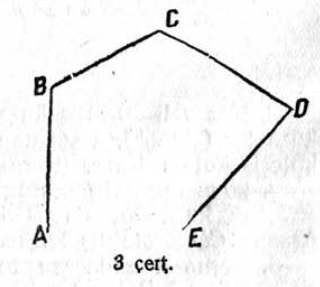
16. 4 чертёж вылын сетӧма воздушнӧй сообщенньӧяслысь карта. Чегсьӧмъясӧс веськӧдӧмӧн сравнитны Москвасянь Берлинӧдз да Москвасянь Сухумиӧдз расстоянньӧяс. Масштабӧн пӧльзуйтчӧмӧн тӧдмавны тайӧ расстоянньӧяслысь кузьтаяссӧ.

Чутъяс да веськыд визьяс. Налӧн мӧда-мӧдкӧд расположенньӧ.

17. Тӧдмавны, куйлӧны‐ӧ A, B да C чутъяс ӧти веськыд визь вылын, кор на костын расстоянньӧяс татшӧмӧсь:

1) AB = 20 м, AC = 13 м, BC = 7 м.

2) AB = 4 м, AC = 7 м, BC = 3 м.

3) AB = 1,8 м, AC = 1,3 м, BC = 3 м.

18. 1) Сетӧма 3 чут, кодъяс оз куйлыны ӧти веськыд визь вылын. Тӧдмавны, кымын различнӧй веськыд визь позьӧ нуӧдны тайӧ чутъяс пыр найӧс гозйӧн-гозйӧн босьтігӧн.

2) Кымын веськыд визьӧн позьӧ ӧтлаавны гозйӧн-гозйӧн 4 чутӧс, кодъяс пиысь некутшӧм 3 чут оз куйлыны ӧти веськыд визь вылын?

Тайӧ жӧ юалӧм 5 чут йылысь? 20 чут йылысь? n чут йылысь?

2 §. Пельӧсъяс.

Пельӧсъясӧс вӧчӧм, мурталӧм да на вылын действийӧяс.

1. Вӧчны сетӧм пельӧс ыджда пельӧс да муртавны сійӧс транспортирӧн.

2. Транспортир отсӧгӧн вӧчны 60°; 75°; 125°; 150° ыджда пельӧсъяс.

3. Вӧчны син серти 30°; 45°; 120° да 135°‐а пельӧсъяс да прӧверитны найӧс транспортирӧн.

4. Вӧчны кык сетӧм пельӧс сумма ыджда пельӧс.

5. Корсьны куим сетӧм пельӧслысь сумма.

6. Корсьны сумма пельӧсъяслысь: 1) 45°36′ да 78°57′; 2) 26°16′45″ да 117°52′30″; 3) 15°40′, 37°50′30″, 88°0′45″ да 20°30′40″.

7. Вӧчны кык сетӧм пельӧс разносьт ыджда пельӧс.

8. Корсьны разносьт пельӧсъяслысь: 1) 96°35′15″ да 48°45′45″; 2) 71°10′ да 29°52′30″; 3) 153°17′42″ да 68°29′.

9. Корсьны веськыд пельӧсӧдз содтӧд со кутшӧм ёсь пельӧсъяс дінӧ: 1) 70°; 2) 34°23′; 3) 22°42′38″.

10. Сетӧма кык пельӧслысь суммасӧ да разносьтсӧ. Вӧчны тайӧ пельӧсъяс.

11. Сетӧм ёсь пельӧсӧс ыдждӧдны 3 пӧв.

12. Корсьны произведенньӧяс: 1) 35°42′⋅5; 2) 17°23′45″⋅4; 3) 55°32′30″⋅3.

13. Сетӧм пельӧсӧс юкны 2, 4, 8, 16 ӧтыджда юкӧнъяс вылӧ.

14. Корсьны частнӧй: 1) 93°15′ : 3; 2) 147°45′ : 2; 3) 98°21′50″ : 4; 4) 161°0′40″ : 8.

15. Вӧчны ёсь да тшӧтшыд пельӧс. Тӧдмавны, кымынысь ёсь пельӧс тӧрӧ тшӧтшыдас.

16. Корсьны частнӧй: 1) 105° : 30°; 2) 66°55′ : 24°20′; 3) 28°35′ : 40°50′.

Бердса пельӧсъяс.

17. Тшӧтшыд пельӧс пытшкын йывсяньыс сійӧ бокъяс дінӧ сувтӧдӧма перпендикуляръяс; тайӧ перпендикуляръяс костын пельӧсыс 4⁄7d ыджда. Определитны тшӧтшыд пельӧссӧ. Транспортирӧн пӧльзуйтчӧмӧн вӧчны точнӧй чертёж.

18. Сетӧма кык бердса пельӧс: ёсь да тшӧтшыд. Найӧ йыв пырыс ӧтувъя бок дінӧ перпендикулярнӧя нуӧдӧма веськыд визь, коді пӧлыньтчӧма ёсь пельӧсса мӧд боксяньыс 5⁄7d вылӧ, а тшӧтшыд пельӧсса мӧд боксяньыс 3⁄7d вылӧ. Корсьны сетӧм пельӧсъяслысь суммасӧ да вӧчны точнӧй чертёж.

Орчча пельӧсъяс.

19. Кӧрт туй станцияын запаснӧй туй главнӧй туйсьыс кежӧ 20°-а пельӧс улын. Чертитны туйясыслысь расположенньӧсӧ.

20. Вӧчны пельӧс, коді сетӧм ABC пельӧскӧд суммаын сетӧ 2 веськыд пельӧс.

21. AB веськыд визь вылын босьтӧма C чут; сысянь нуӧдӧма CD луч сідз, мый ACD пельӧс BCD пельӧсысь 4 пӧв ыджыдджык. Определитны тайӧ пельӧсъяслысь ыдждаяссӧ.

22. Определитны 2 орчча пельӧс, кодъяс пиын ӧтиыс 2⁄9d-ӧн ыджыдджык мӧдсьыс.

23. Определитны пельӧс, коді ас орччасьыс серти 3⁄7 ыджда.

24. ABC да DBC кык дорвыв пельӧс пиысь ABC пельӧс 108° ыджда, а мӧдыс 1½ пӧв сыысь ичӧтджык. Составитӧны-ӧ ӧти веськыд визь BA да BD бокъяс?

25. Кык дорвыв пельӧслӧн отношенньӧыс 7 : 3, а разносьтыс 72° ыджда. Лоӧны-ӧ тайӧ пельӧсъясыс орчча пельӧсъясӧн?

26. ABC да CBD пельӧсъяс орччаӧсь. CBD пельӧс = 0,375d. Определитны пельӧс, коді артмӧ B чутысь AB веськыд дінӧ сувтӧдӧм перпендикуляр да ABC пельӧсса биссектриса костын. Вӧчны чертёж.

27. Докажитны, мый орчча пельӧсъяслӧн биссектрисаяс мӧда‐мӧдыслы перпендикулярнӧйӧсь.

28. Определитны 2 бердса пельӧс AOB да BOC, кор тӧдам, мый налӧн суммаыс 216° ыджда да AO боклӧн йыв сайӧ нюжӧдӧмыс BOC пельӧсӧс юкӧ шӧри. Вӧчны точнӧй чертёж.

Веськыд визь ӧтар бокын расположеннӧй ӧтувъя йыла пельӧсъяс.

29. Сетӧма нёль бердса пельӧс, кодъяслӧн боквывса бокъясыс мед составитӧны ӧти веськыд визь. Быд водзвывса пельӧс 1⁄9d-ӧн ыджыдджык бӧръясьыс. Определитны да вӧчны тайӧ пельӧсъяс.

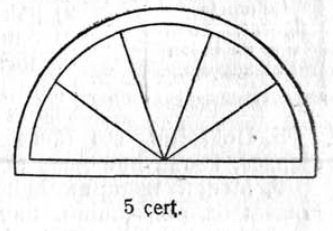
30. Ӧшиньлӧн вылыс юкӧныс 5 чертёж вылын сетӧм сикаса. Определитны, кымын градуса пельӧсъяс лоӧны быд луч костын.

Веськыд визь кыкнан бокын расположеннӧй ӧтувъя йыла пельӧсъяс.

31. Кымын градус кӧлеса паличьяскостса пельӧсын, кор кӧлесаын 18 палич? 16 палич?

32. ABC пельӧс 6⁄11d ыджда; B йылысь ABC пельӧс ортсыті нуӧдӧма BA да BC бокъяссянь ӧтмоза пӧлыньӧн BD луч. Определитны тайӧ пӧлыньтчӧмлысь ыдждасӧ.

33. Нёль пельӧс, кодъяс артмӧны ӧти чутысь петан 4 лучӧн, сэтшӧмӧсь, мый быд визьвывса пельӧс 2 пӧв бӧръясьыс ыджыдджык. Корсьны быд пельӧслысь ыдждасӧ да вӧчны тайӧ пельӧсъяссӧ.

Противоположнӧй (вертикальнӧй) пельӧсъяс.

34. Кык вомӧнассян веськыд визьясӧн артман нёль пельӧс пиысь ӧти 3⁄5d ыджда. Ыджыдӧсь-ӧ мукӧд пельӧсъясыс?

35. Сӧмын линейкаӧн вӧчны пельӧс, медым сійӧ вӧлі сетӧм пельӧс ыджда да сыкӧд ӧтувъя йыла.

36. AB да CD веськыдъяс вомӧнассьӧны O чутын. AOD да COB пельӧсъяслӧн суммаыс 220° ыджда. Определитны AOC пельӧс.

37. Сетӧм пельӧслӧн да сыкӧд кык орчча пельӧсъяслӧн суммаыс 2⅜d. Определитны сетӧм пельӧс.

3 §. Куимпельӧсаяс да унапельӧсаяс. Перпендикуляръяс да пӧлыняяс. Осевӧй симметрия.

Кык ӧткузя бока куимпельӧса.

1. Вӧчны кык ӧткузя бока куимпельӧса:

1) подувтас да боквывса бок серти;

2) подувтас да сы бердса пельӧс серти;

3) боквывса бок да йывбердса пельӧс серти;

4) боквывса бок да подувтасбердса пельӧс серти.

2. Кык ӧткузя бока куимпельӧсаын боквывса бок вылӧ вӧчӧма ӧткузя бокъяса куимпельӧса; тайӧ мӧд куимпельӧсалӧн периметр 45 м ыджда, а первой куимпельӧсалӧн периметрыс 40 м. Определитны сетӧм куимпельӧсалысь подувтассӧ.

Куимпельӧсаясӧс вӧчӧм да налӧн равенство.

3. Вӧчны куимпельӧса:

1) бок да сы бердса кык пельӧс серти;

2) кык бок да на костса пельӧс серти;

3) куим бок серти.

4. Кык ӧткузя бока куимпельӧсаын подувтасбердса пельӧсъяслӧн биссектрисаяс ӧтыдждаӧсь. Докажитны.

5. Докажитны, мый кык ӧткузя бока куимпельӧсаын боквывса бокъяс вылӧ нуӧдӧм медианаяс ӧтыдждаӧсь.

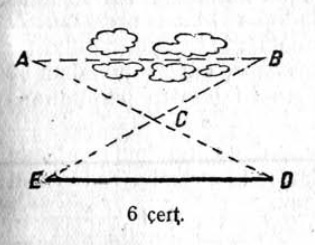
6. Медым муртавны расстоянньӧ A чутсянь B чутӧдз, кодъяс костӧд он письты мунны мернӧй чептӧн (6 чертёж), бӧрйӧны сэтшӧм C чут, кысянь медым вӧлі тыдалӧны эськӧ кыдз A чут, сідз жӧ и B чут; провешивайтӧны AC да BC; нюжӧдӧны найӧс C чут сайӧ да мурталӧны CD = AC да EC = CB. Сэк ED вундӧг лоӧ корсян AB расстоянньӧ ыджда. Мый вӧсна?

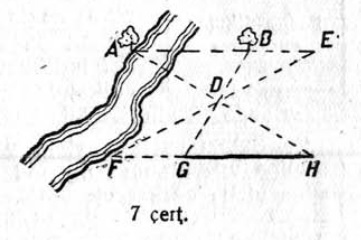
7. Медым муртавны расстоянньӧ A чутсянь B чутӧдз, кодъяс пиысь ӧти дінас (A чут) он вермы мунны, провешивайтӧны AB вундӧг (7 чертёж) да сійӧс нюжӧдӧм вылын мурталӧны произвольнӧй BE вундӧг. Бӧрйӧны D чут, кысянь медым вӧлі тыдалӧ A чут да позьӧ мунны B да E чутъяс дінӧ. Провешивайтӧны BDG да EDF веськыдъяс да мурталӧны FD = DE да DG = BD. Сэсся мунӧны FG веськыд визь кузя A чут вылӧ видзӧдӧмӧн, кытчӧдз оз сюр сэтшӧм H чут, коді медым вӧлі куйлӧ AD веськыд вылын. Сэк GH лоӧ корсян расстоянньӧ ыджда. Докажитны.

8. Ӧткузя бокъяса ABC куимпельӧсаын быд бок кузя пуктӧма ӧтыджда вундӧгъяс AB₁ = BC₁ = CA₁. A₁, B₁ да C₁ чутъяссӧ ӧтлаалӧма веськыдъясӧн. Докажитны, мый A₁B₁C₁ куимпельӧса сідзжӧ ӧткузя бокъяса.

9. Ӧткузя бокъяса ABC куимпельӧсалысь быд бок нюжӧдӧма: AB — B йыв сайӧ, BC нюжӧдӧма C йыв сайӧ, CA нюжӧдӧма A йыв сайӧ. Найӧс нюжӧдӧмъяс вылын пукталӧма ӧткузя вундӧгъяс да налысь помъяссӧ мӧда-мӧдыскӧд ӧтлаавлӧма. Определитны артмӧм куимпельӧсалысь сикассӧ.

10. 1) Вӧчны куимпельӧса кык бок серти да пельӧс серти, коді куйлӧ ыджыдджык боклы паныд.

2) Докажитны теорема: ӧти куимпельӧсалӧн кӧ кык бок да на пиысь ыджыдджыкыслы паныда пельӧс соответственнӧя ӧтыдждаӧсь мӧд куимпельӧсаса кык боккӧд да на пиысь ыджыдджыкыслы паныда пельӧскӧд, сэк куимпельӧсаяс ӧтыдждаӧсь.

11. 1) Вӧчны куимпельӧсаӧс кык бок серти да пельӧс серти, коді куйлӧ ичӧтджык бокыслы паныд.

2) Петкӧдлыны, мый ӧти куимпельӧсалӧн кӧ кык бок да на пиысь ичӧтджыкыслы паныда пельӧс соответственнӧя ӧтыдждаӧсь мӧд куимпельӧсаса кык боккӧд да на пиысь ичӧтджыкыслы паныда пельӧскӧд, куимпельӧсаяс вермасны лоны кыдз ӧтыдждаӧн, сідзи и не ӧтыдждаӧн.

12. Докажитны теорема: ӧти куимпельӧсалӧн кӧ 2 бок да медиана соответственнӧя ӧтыдждаӧсь мӧд куимпельӧсаса кык боккӧд да медианакӧд, то татшӧм куимпельӧсаяс ӧтыдждаӧсь. Видзӧдлыны кык случай: 1) кор медианасӧ нуӧдӧма сетӧм бокъяс пиысь кодаскӧ ӧти бокас; 2) кор медианасӧ нуӧдӧма сетӧм бокъяс костті.

Куимпельӧсаын бокъяс костын зависимосьт.

13. Вермас-ӧ лоны татшӧм бокъяса куимпельӧса: 1) 5 м, 10 м, 12 м; 2) 1 м, 2 м, 3,3 м; 3) 1,2 м, 1 м, 2,2 м?

14. Вермасны-ӧ куимпельӧсалӧн бокъяс относитчыны, кыдз: 1) 1 : 2 : 3; 2) 2 : 3 : 4?

15. Куимпельӧсаын ӧти бок = 1,9 м, мӧд = 0,7. Определитны коймӧд боксӧ, кор тӧдам, мый сійӧ кутас муртассьыны дзонь метръясӧн.

16. Кык ӧткузя бока куимпельӧсалӧн периметрыс 1 м ыджда, а подувтас 0,4 м ыджда. Определитны боквывса боклысь кузьтасӧ.

17. Кык ӧткузя бока куимпельӧсалӧн ӧти бокыс 25 м, а мӧдыс — 10 м. Кодыс на пиысь лоӧ подувтасӧн?

18. Кык ӧткузя бока куимпельӧсаын боквывса бок дінӧ нуӧдӧм медиана юкӧ сылысь периметрсӧ 15 см да 6 см ыджда юкӧнъясӧ. Определитны бокъяссӧ куимпельӧсалысь.

19. Докажитны, мый куимпельӧсаын бокыс периметр джынйысь ичӧтджык.

20. Докажитны, мый куимпельӧсаын кутшӧмкӧ чутсянь, кодӧс босьтӧма куимпельӧса пытшкас, йывъясӧдзыс расстоянньӧяслӧн сумма 1) периметрсьыс ичӧтджык, но 2) периметр джынсьыс ыджыдджык.

21. ABC куимпельӧса пытшкын BC бокӧ нуӧдӧма веськыд AD визь сідз, мый CAD пельӧс ACD пельӧс ыджда. ABC да ABD куимпельӧсаяслӧн периметръясыс 37 м да 24 м ыдждаӧсь. Определитны AC-лысь кузьтасӧ.

22. Кык ӧткузя бока ABC куимпельӧсаын нуӧдӧма BD судта. ABC куимпельӧсалӧн периметр 50 м. ABD куимпельӧсалӧн периметр 40 м. Определитны BD судтасӧ.

Перпендикуляр да пӧлыняяс

23. Кык ӧткузя бока ABC куимпельӧсаын AB бокыс 14 см ыджда; сійӧ D шӧрсьыс сувтӧдӧма BC боккӧд вомӧнасьтӧдз сылы^AB‐лы. — А.В./^ DE перпендикуляр; E чутсӧ ӧтлаалӧма A-кӧд; AEC куимпельӧсалӧн периметрыс 24 см. Определитны AC-лысь кузьтасӧ.

24. Ӧти чутысь сетӧм веськыд визьӧ нуӧдӧма 2 ӧтыджда пӧлыня; найӧ подувтасъяскостса расстоянньӧыс 16 м ыджда. Определитны быд пӧлынялысь сетӧм веськыд вылӧ проекциясӧ.

Веськыд пельӧса куимпельӧсаясӧс вӧчӧм да налӧн равенство.

25. Вӧчны веськыд пельӧса куимпельӧсаӧс:

1) кык катет серти;

2) катет да гипотенуза серти;

3) катет да ёсь пельӧс серти;

4) гипотенуза да ёсь пельӧс серти.

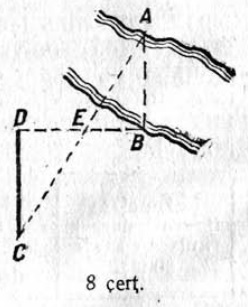
26. Медым муртавны, ылын-ӧ A пунктсянь B пунктӧдз (A пунктыс ю ӧтар пӧлын, а B пунктыс — мӧдар пӧлас), эккер отсӧгӧн провешивайтӧны AB‐лы перпендикулярнӧя определённӧй кузьтаа BD вундӧг (8 чертёж). BD вундӧгсӧ E чутын юкӧны шӧри. D чутӧ BD-лы сувтӧдӧны DC перпендикуляр; мунӧны DC кузя A вылӧ видзӧдӧмӧн C чутӧдз, коді куйлӧ AE веськыд визь вылын. DC-лӧн кузьта AB ыджда. Докажитны.

27. 1) Докажитны, мый пельӧс биссектрисалы перпендикулярнӧй веськыд визь вундӧ пельӧс бокъясысь ӧтыджда вундӧгъяс.

2) Пельӧс пытшкын либӧ сы сайын сетӧм чут пыр нуӧдны сэтшӧм веськыд визь, коді медым пельӧс бокъясысь вундіс ӧтыджда юкӧнъяс.

28. 1) Докажитны, мый кык ӧткузя бока куимпельӧсаын боквывса бокъясыс вылӧ лэдзӧм судтаяс ӧтыдждаӧсь.

2) Составитны мӧдара теорема да докажитны сійӧс.

29. Куим сикт A, B да C оз сулавны ӧти веськыд визь вылын. Чертёж вылын индыны, кыдз A-сянь нуӧдны веськыд туй, медым сыӧдз B да C сиктъяссянь расстоянньӧыс вӧлі ӧткодь.

30. AB веськыд визь ӧтар сайын сетӧма кык чут: M да N. AB веськыд вылысь корсьны сэтшӧм C чут, медым C-ысь сетӧм M да N чутъяс пыр нуӧдӧм CM да CN лучьяс CA да CB лучьяскӧд составитісны ӧтыджда пельӧсъяс.

Чутъяслӧн геометрическӧй местаяс.

31. Сетӧма ABC куимпельӧса. A пельӧсса биссектриса вылысь корсьны B да C йывъяссянь ӧтылнаӧ ылысмӧм чут.

32. Корсьны куимпельӧсаса став йывъяссянь ӧтылнаӧ ылысмӧм чут. Пыр-ӧ тайӧ чут лоӧ куимпельӧса пытшкын?

33. Сетӧма пельӧс да сы пытшкын M чут. Корсьны сэтшӧм чут, коді медым вӧлі ӧтылнаын пельӧс кыкнан боксяньыс да M чутсянь вӧлі сетӧм a расстоянньӧ сайын.

34. Куимпельӧсаса бок вылысь корсьны сэтшӧм чут, кысянь эськӧ вӧлі мӧд кык бокъясӧдзыс ӧтылнаын.

35. Куимпельӧсаын аддзыны куимнан боксяньыс ӧтылнаӧ ылысмӧм чут.

36. Сетӧма A пельӧс да чутъяс B да C, кодъяс пиысь ӧтиыс куйлӧ ӧти бок вылас, а мӧдыс — мӧд вылас. Корсьны:

1) M чут, коді медым вӧлі пельӧс боксяньыс ӧтылнаын да мед удовлетворяйтіс условйӧлы, мый MC = MB;

2) N чут, коді медым вӧлі куйлӧ пельӧс ӧти бок вылас^Оз лӧсяв вочакывкӧд (оригиналын тшӧтш). Колӧ, медым N вӧлі пельӧс боксяньыс ӧтылнаын. — А.В./^ да та дырйи медым NC = CB.

3) Сэтшӧм P чут, медым B да C чутъяс вӧліны A да P-сянь ӧтылнаынӧсь^Стӧчджыка кӧ: AB = PB, AC = PC. — А.В./^.

37. Сетӧма A пельӧс да ӧти бок вылас B чут. Мӧд бок вывсьыс корсьны сэтшӧм C чут, медым CA + CB сумма вӧлі сетӧм l кузьта.

Нёльпельӧсаяс.

38. Определитны нёльпельӧсалысь бокъяссӧ, кор найӧ относитчӧны кыдз 2 : 5 : 4 : 8, а сылӧн периметрыс 76 м ыджда.

39. Нёльпельӧсалӧн бокъяс вермасны-ӧ относитчыны кыдз 2 : 3 : 4 : 10?

40. 1) Вӧчны нёльпельӧса, кодлӧн бокъясыс 1 см, 2 см, 3 см да 4 см, а первой да нёльӧд бок костті мунысь диагональ 2,6 см ыджда.

2) Вӧчны нёльпельӧса сійӧ жӧ нёль бок серти, кодъяс 1,2 см, 1,8 см, 2,4 см да 3,0 см ыдждаӧсь, да мӧд да коймӧд бокъяс костын 102°-а пельӧс серти.

41. Нёльпельӧсаӧс юкӧма диагональӧн 2 куимпельӧса вылӧ, кодъяслӧн периметръясыс 25 м да 27 м; нёльпельӧсалӧн периметр 32 м. Корсьны нуӧдӧм диагональлысь кузьтасӧ.

Унапельӧсаяс.

42. Кымын диагональ позьӧ нуӧдны ӧти йывсянь: 1) витпельӧсаын, 2) даспельӧсаын, 3) n‐пельӧсаын?

43. Кымын куимпельӧса артмас, нуӧдны кӧ став диагональяссӧ ӧти йылысь: 1) квайтпельӧсаын, 2) кӧкъямыспельӧсаын, 3) n‐пельӧсаын?

44. Кымын диагональ позьӧ нуӧдны: 1) витпельӧсаын, 2) даспельӧсаын, 3) n‐пельӧсаын?

45. Кымын бок унапельӧсаын, налӧн кӧ лыдыс ӧти йывсянь нуӧдӧм диагональяс лыдысь m пӧв унджык? (m = 2; 4; 5).

46. Кымын бок унапельӧсаын, став диагональясыслӧн кӧ лыдыс бокъяс лыдсьыс m пӧв унджык? (m = 0,5; 1; 2; 2,5).

Осевӧй симметрия.

47. Вӧчны вундӧгӧс, сетӧм симметрия ось серти сетӧм вундӧглы симметричнӧйӧс.

48. Сетӧм веськыд пельӧса куимпельӧсаӧс содтыны симметрияӧдз: 1) ӧти катет серти; 2) мӧд катет серти; 3) гипотенуза серти.

49. Сетӧма симметрия ось да кытшвизь. Вӧчны сылы симметричнӧй кытшвизь.

50. Сетӧма симметрия ось да чегласьӧм визь. Вӧчны сетӧм чегласьӧмлы симметричнӧй мӧд чегласьӧм.

4 §. Параллельнӧй веськыд визьяс. Куимпельӧсаын да унапельӧсаын пельӧсъяслӧн сумма.

Параллельнӧйяс да вомӧналысь бердса пельӧсъяс.

1. Кык параллельнӧй веськыд визьӧс вомӧналӧма коймӧдӧн. Индӧма, мый артмӧм кӧкъямыс пельӧс пиысь ӧтиыс 72° ыджда. Ыджыд-ӧ быд пельӧс?

2. Кык веськыд параллельнӧй вомӧналӧмаӧсь коймӧдӧн; ӧти пытшкӧс пельӧсъяс пиысь 1⅜d ыджда. Кутшӧм пельӧс улын сылӧн биссектрисаыс вомӧналӧ мӧд параллельсӧ?

3. Кык веськыд параллельнӧй вомӧнассьӧны коймӧдӧн. Куим пельӧслӧн сумма: сетӧм пытшкӧссалӧн, сылӧн пытшкӧсса ӧтарбоксаыслӧн да первойыскӧд крестӧн куйлысьыслӧн 3​2⁄7d ыджда. Определитны сетӧм пытшкӧс пельӧслы соответственнӧй пельӧс.

4. AMB да CND веськыд визьясӧс вомӧналӧма EMNF веськыд визь, ∠CNF = 3⁄16d да ∠NMB = ¾d. Параллельнӧйӧсь-ӧ сетӧм веськыдъясыс? Кыдз колӧ вежны NMB пельӧслысь ыдждасӧ, медым найӧ лоины параллельнӧйӧсь?

5. AMNB да CRSD веськыдъясӧс вомӧналӧмаӧсь EMRF да GNSH веськыдъясӧн. Сетӧма: ∠AME = 1​5⁄24d; ∠ANS = 1⅜d да ∠MRS = 19⁄24d. Определитны ∠DSH.

Параллельнӧй бокъяса да перпендикулярнӧй бокъяса пельӧсъяс.

6. Сетӧма ∠ABC = 43°. Тайӧ пельӧс пытшкын P чутысь нуӧдӧма бокъясыслы параллельнӧя накӧд вомӧнассьытӧдз 2 веськыдӧс. Определитны артмӧм нёльпельӧсалысь пельӧсъяссӧ.

7. Сетӧма параллельнӧй бокъяса кык пельӧс; на пиысь ӧтиыс мӧдсьыс 90°-ӧн ыджыдджык. Ыджыд-ӧ быд пельӧс?

8. Сетӧма перпендикулярнӧй бокъяса 2 пельӧс; на пиысь ӧтиыс мӧдсьыс 4 пӧв ичӧтджык. Корсьны быд пельӧслысь ыдждасӧ.

9. Куимпельӧсаын подув помъяс пырыс нуӧдӧма боквывса бокъясыслы 2 перпендикуляр, кодъяс вомӧнассигас артмӧдӧны 130°-а пельӧс. Артавны куимпельӧсалысь йывса пельӧссӧ.

Куимпельӧсаын пельӧсъяслӧн сумма.

10. Куимпельӧсаын ӧти пельӧс 1⅙d ыджда, а мӧд — ⅜d. Ыджыд-ӧ коймӧд пельӧсыс?

11. Определитны куимпельӧсалысь пельӧсъяссӧ, найӧ кӧ относитчӧны кыдз 1 : 2 : 3.

12. Куимпельӧсаын кык пельӧс относитчӧны кыдз 5 : 7, а коймӧд пельӧсыс 4⁄19d-ӧн ыджыдджык первойсьыс. Тӧдмавны коймӧд пельӧссӧ.

13. Куимпельӧсаын кык пельӧс 110°23′50″ да 24°36′40″ ыдждаӧсь. Тӧдмавны коймӧдсӧ.

14. Веськыд пельӧса куимпельӧсаын ӧти ёсь пельӧсыс 58°20′ ыджда. Тӧдмавны мӧд ёсь пельӧссӧ.

Кык ӧткузя бока куимпельӧса.

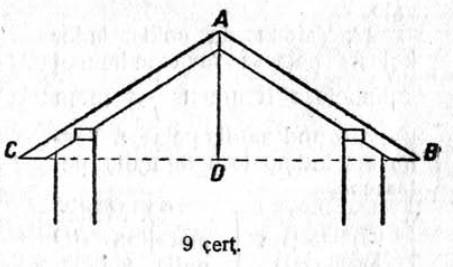
15. СССР шӧр полосаын AC да AB стрӧпилӧяс кост пельӧсъяслысь размеръяссӧ вӧчӧны та ыдждаӧс кымын (9 чертёж):

кӧрт вевтлы 120°

толь „ 145°

черепичалы „ 100°

тьӧслы „ 90°

идзаслы „ 60°

Быд пельӧс вевтлы определитны сійӧ пельӧс, коді артмӧ стрӧпилӧ да горизонтальнӧй CB визь костын.

16. Кык ӧткузя бока куимпельӧсаын йывбердса пельӧсыс 105°0′27″ ыджда. Тӧдмавны подувтасбердса пельӧссӧ.

17. Кык ӧткузя бока куимпельӧсаын подувтасбердса пельӧсыс 70°43′ ыджда. Тӧдмавны йывбердса пельӧссӧ.

18. Кык ӧткузя бока куимпельӧсаын йывбердса пельӧсыс 1​2⁄7d ыджда. Определитны подувтасбердса пельӧссӧ.

19. Кык ӧткузя бока куимпельӧсаын подувтасбердса пельӧсыс 5⁄9d ыджда. Определитны йывбердса пельӧссӧ.

20. Кык ӧткузя бока куимпельӧсаын йывбердса пельӧсыс 30° ыджда; боквывса бок вылас лэдзӧма судта. Корсьны тайӧ судта да подувтас костса пельӧслысь ыдждасӧ.

21. Кык ӧткузя бока куимпельӧсаын подувтасбердса пельӧсыс 30° ыджда; корсьны ыдждасӧ пельӧслысь, коді артмӧ боквывса ӧти бок да боквывса мӧд бок вылӧ лэдзӧм судта костын^бок да судта костын. — А.В./^.

22. Кык ӧткузя бока куимпельӧсаын судта^подувтаслань нуӧдӧм судта. — А.В./^ да боквывса бок костын пельӧс подувтасбердса пельӧссьыс 1⁄7d-ӧн ичӧтджык. Определитны тайӧ куимпельӧсалысь пельӧсъяссӧ.

Веськыд пельӧса куимпельӧса.

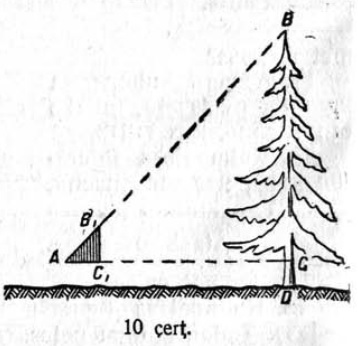
23. Сы могысь, медым пулысь муртавны BD джудждасӧ, вӧчисны веськыд пельӧса AB₁C₁ куимпельӧса, кӧн ∠A = 45° (10 чертёж). Сійӧс вертикальнӧя кутӧмӧн пусянь мунісны сы ылнаӧдз, кытчӧдз AB гипотенуза кузя видзӧдігӧн эз аддзыны пулысь B йывсӧ. Кутшӧм пуыслӧн джудждаыс, AC расстоянньӧ кӧ = 5,6 м, а мортлӧн джудждаыс = 1,7 м?

24. 1) Веськыд пельӧса куимпельӧсаын ӧти ёсь пельӧс ½d ыджда. Катетъяслӧн суммаыс 36 см. Определитны найӧс.

2) Веськыд пельӧса куимпельӧсаын ёсь пельӧсыс ½d ыджда. Определитны гипотенузасӧ, сылы соответствуйтысь судтанас кӧ суммаыс лоӧ 12 см.

30°-а пельӧслы воча куйлысь катет.

25. Докажитны теорема: веськыд пельӧса куимпельӧсаын кӧ ӧти ёсь пельӧс 30° ыджда, сылы воча куйлысь катет гипотенуза джын ыджда.

26. Мӧдара теорема (видз. 25 задача): катет кӧ гипотенузаысь кык пӧв дженьыд, сылы воча куйлысь пельӧс 30° ыджда. Докажитны.

27. Циркуль да линейка отсӧгӧн юкны веськыд пельӧсӧс куим ӧтыджда пельӧ.

28. Веськыд пельӧса куимпельӧсаын ёсь пельӧсъяс пиысь ӧтиыс ⅔d ыджда, а гипотенузалӧн да ичӧтджык катетыслӧн суммаыс 1,8 м. Определитны гипотенузасӧ.

Куимпельӧсалӧн ортсыса пельӧс.

29. ABC куимпельӧсаын B йывбердса ортсыса пельӧсыс A пельӧсысь 3 пӧв ыджыдджык да C пельӧсысь 4⁄9d-ӧн ыджыдджык. Определитны куимпельӧсалысь пельӧсъяссӧ.

30. Ӧткузя бокъяса куимпельӧсаын нуӧдӧма 2 медиана; корсьны на костса ёсь пельӧссӧ.

31. Веськыд пельӧса куимпельӧсаын ёсь пельӧсъяс пиысь ӧтиыс d/3 ыджда; определитны ёсь пельӧссӧ, коді артмӧ гипотенуза да веськыд пельӧсса биссектриса костын.

32. Кык ӧткузя бока куимпельӧсаын пытшкӧс пельӧсъяслӧн кутшӧмкӧ ӧти ортсыса пельӧскӧд суммаыс 21⁄8d ыджда. Определитны тайӧ куимпельӧсалысь пельӧсъяссӧ.

33. Докажитны, мый кык ӧткузя бока куимпельӧсаын йывдінса ортсыса пельӧсыслӧн биссектрисаыс подувтасыслы параллельнӧй.

Куимпельӧсаса пельӧсъяс сумма йылысь теорема куимпельӧсаяс вылӧ разнӧй задачаяс решитӧм вылӧ применитӧм.

34. Куимпельӧсаын пельӧсъяс пиысь ӧти пельӧс ⅔d ыджда; мӧд кык пельӧсъяссянь нуӧдӧмаӧсь биссектрисаясӧс. Ыджыд-ӧ ёсь пельӧсыс, коді артмӧ тайӧ биссектрисаясӧн?

35. Сетӧма A пельӧс; йывсяньыс бок кузяыс пуктам AB вундӧг; B чутысь нуӧдам сетӧм пельӧс мӧд бокыслы параллельнӧй веськыдӧс; тайӧ параллельнӧй вылӧ пуктам BA ыджда BD вундӧг; D чут ӧтлаалам A йывкӧд. Докажитны, мый AD веськыд визь сетӧм пельӧссӧ юкӧ шӧри.

36. Кутшӧм пельӧс улын вомӧнассьӧны параллельнӧй веськыдъясбердса кык пытшкӧс ӧтарбокса пельӧсъяслӧн биссектрисаясыс?

37. ABC куимпельӧсаын B пельӧсыс веськыд. M чут лоӧ A да C пельӧсъясса биссектрисаяслӧн вомӧнассян чут. Определитны AMC пельӧс.

38. ABC куимпельӧсаын M чутын вомӧнассьӧны A да C пельӧсъяслӧн биссектрисаясыс. Определитны ABC пельӧссӧ, кор сійӧ AMC пельӧс джын ыджда.

39. ABC куимпельӧсаын B пельӧсыс веськыд; AD да CE лоӧны AC гипотенузалӧн нюжӧдӧмъяс. BAD да BCE пельӧсъяссӧ юкӧма шӧри; M — найӧ биссектрисаяслӧн вомӧнассянін чут (биссектрисаяссӧ нюжӧдӧма йыв саяс). Определитны AMC пельӧс.

40. Кык ӧткузя бока куимпельӧсалӧн подувтас да бокса судта костса пельӧсыс 8⁄15d ыджда. Определитны тайӧ куимпельӧсалысь пельӧсъяссӧ.

41. Кык ӧткузя бока ABC куимпельӧсаын бокса AD судтаыс AB боквывса бокыскӧд вӧчӧ BAD пельӧс = ⅕d ыджда. Определитны тайӧ куимпельӧсалысь пельӧсъяссӧ: 1) кор AD судтаыс мунӧ куимпельӧса пытштіыс, 2) кор AD судтаыс мунӧ куимпельӧса сайті.

42. Докажитны, мый веськыд пельӧса куимпельӧсаын гипотенуза дінӧ нуӧдӧм медиана гипотенуза джын ыджда.

43. Докажитны мӧдара теорема (видз. 42 задача): медианаыс кӧ сійӧ бок джын ыдждаыс, код дінӧ сійӧс нуӧдӧма, куимпельӧса эм веськыд пельӧса.

44. Кык ӧткузя бока веськыд пельӧса BAC куимпельӧсаын кӧ BC гипотенуза вылын босьтны E да D кык чут сідз, мый BE = BA да CD = CA, сэки ∠DAE = ½d. Докажитны.

45. ABC лоӧ AC подувтаса кык ӧткузя бока куимпельӧса; CD — C пельӧслӧн биссектриса; ∠ADC = 5⁄3d ыджда. Определитны ∠B.

46. Кык ӧткузя бока куимпельӧсаын йывбердса пельӧсыс = 36° ыджда. Докажитны, мый подувтасбердса пельӧслӧн воча боккӧд вомӧнасьтӧдз нюжӧдӧм биссектрисаыс кык ӧткузя бока куимпельӧсасӧ юкӧ кык куимпельӧсаӧ, кодъяс сідзжӧ лоӧны кык ӧткузя бокъясаӧсь.

47. ABC куимпельӧсаын AC боксӧ нюжӧдӧма C чут сайӧ CE = CB кузьтаӧ да A чут сайӧ AD = AB кузьтаӧ; E да D чутъяссӧ ӧтлаалӧма B‐кӧд. Определитны DBE куимпельӧсалысь пельӧсъяссӧ ABC куимпельӧсаын соответствуйтысь пельӧсъяс пыр.

48. ABC куимпельӧсаын нуӧдӧма AD да CE судтаяс, M чут налӧн вомӧнассянін. Определитны ∠AMC, ∠BAC кӧ = ¼d ыджда да ∠BCA = ⅚d ыджда.

49. ABC кык ӧткузя бока куимпельӧсаын AD да CE бокса судтаясыс вӧчӧны ∠AMC = 8⁄15d. Определитны ABC куимпельӧсалысь пельӧсъяссӧ.

50. ABC куимпельӧсаын C йывсьыс нуӧдӧма ортсыса пельӧс да пытшкӧсса пельӧс биссектрисаяс; первой биссектрисаыс AB бокыскӧд вӧчӧ 6⁄17d ыджда пельӧс. Кутшӧм пельӧс артмӧ мӧд биссектрисаӧн да AB боксӧ нюжӧдӧмӧн?

51. Гипотенуза шӧрӧ сувтӧдӧма катеткӧд вомӧнассьытӧдз перпендикуляр, артман чутсӧ ӧтлаалӧма мӧд катет помкӧд, да тайӧ вундӧгыс куимпельӧсалысь пельӧссӧ юкӧ 2 : 5 отношенньӧын (ичӧтджык юкӧныс гипотенуза бердын). Определитны тайӧ пельӧссӧ.

Унапельӧсаын пельӧсъяслӧн сумма

52. Определитны пытшкӧсса пельӧсъяслысь суммасӧ: 1) сизимпельӧсалысь; 2) даспельӧсалысь; 3) кызьвитпельӧсалысь.

53. Определитны витпельӧсалысь пельӧсъяссӧ, кор налӧн величинаясыс относитчӧны кыдз 1 : 1,5 : 2 : 2,5 : 3.

54. Кыдз вежсяс унапельӧсалӧн пельӧсъяс суммаыс, бокъяс лыдсӧ кӧ ыдждӧдны 5 вылӧ?

55. Кымын бок унапельӧсалӧн, пытшкӧс пельӧсъясыслӧн кӧ суммаыс 1) 30d; 2) 48d; 3) 57d ыдждаӧсь.

56. Кутшӧм унапельӧсаын пытшкӧс пельӧсъяслӧн суммаыс ортсыса пельӧсъяс суммаыс ыджда?

57. Кымын бок унапельӧсалӧн, пытшкӧс пельӧсъясыслӧн кӧ суммаыс тшӧтш кутшӧмкӧ ӧти ортсыса пельӧскӧд 23d ыджда?

58. Определитны унапельӧсалысь бокъяс лыдсӧ, пытшкӧс пельӧсъясыслӧн кӧ суммаыс ортсыса пельӧсъяс суммаысь (ортсыса пельӧсъяссӧ босьтӧма быд йыв бердысь ӧтиӧс) m пӧв ыджыдджык.

59. Определитны нёльпельӧсалысь пельӧсъяссӧ, кодъяс пиысь кӧ первой кыкыс относитчӧны кыдз 5 : 7, коймӧдыс найӧ разносьт ыдждаыс, а нёльӧдыс коймӧдсьыс 4⁄11d-ӧн ичӧтджык.

5 §. Параллелограммъяс да трапецияяс.

Параллелограммлӧн пельӧсъяс да бокъяс.

1. Параллелограммлӧн пельӧсъяс пиысь ӧтиыс 3⁄7d. Определитны мукӧд пельӧсъяссӧ.

2. Определитны параллелограммлысь пельӧсъяссӧ, кодъяс пиысь ӧтиыс мӧдсьыс 3⁄11d-ӧн ыджыдджык.

3. ABCD параллелограммын AB бок = 9 см да став периметр серти 3⁄10 ыджда. Определитны параллелограммлысь мукӧд бокъяссӧ.

4. Параллелограммлӧн кык бок относитчӧны кыдз 3 : 4, а периметрыс 2,8 м ыджда. Определитны параллелограммлысь бокъяссӧ.

5. ABCD параллелограммын нуӧдӧма A пельӧсса биссектриса, коді BC боксӧ вомӧналӧ E чутын. Определитны BE да EC вундӧгъяс, AB‐кӧ = 9 см, а AD = 15 см.

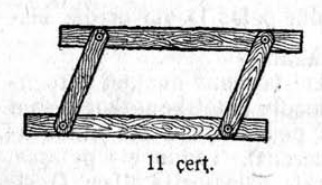
6. Мый вылын подувтасассьӧ «параллельнӧй линейка» нима чертёжнӧй инструментъяслӧн устройствоыс (11 чер.)?

7. Параллелограммлӧн бокъясыс 8 см да 3 см; ыджыдджык боксьыс пельӧсъяслӧн биссектрисаясыс воча боксӧ юкӧны 3 пельӧ. Корсьны тайӧ юкӧнъяссӧ.

Параллелограммлӧн диагональяс.

8. Параллелограммлӧн кӧ кутшӧмкӧ ӧти бок 5 м ыджда, вермасны-ӧ лоны сылӧн диагональясыс 1) 4 м да 6 м; 2) 4 м да 3 м; 3) 6 м да 7 м ыдждаӧн?

9. Докажитны, мый нёльпельӧса, кодлӧн диагональясыс юксьӧны шӧри, эм параллелограмм.

10. Вермас-ӧ лоны, мый параллелограммлӧн диагональыс бокыскӧд ӧтыджда?

11. Параллелограммын диагональяс вомӧнассянін чут пыр нуӧдӧма веськыд визь. Докажитны, мый сылӧн параллельнӧй бокъяскостса вундӧгыс тайӧ чутӧн юксьӧ шӧри.

12. ABCD параллелограммын диагональясыслӧн вомӧнассянін чут пырыс нуӧдӧма веськыд визь, коді BC да AD бокъяс вылын вундӧ вундӧгъяс: BE = 2 м да AF = 2,8 м. Определитны BC да AD бокъяссӧ.

13. ABCD параллелограммын B йывсянь нуӧдӧм судта AD подувтассӧ юкӧ шӧри. Определитны BD диагональ да параллелограммлысь бокъяссӧ, тӧдам кӧ, мый параллелограммлӧн периметр 3,8 м да ABD куимпельӧсаса периметрысь кузьджык 1 м-ӧн.

Параллелограммӧс вӧчӧм.

14. Вӧчны параллелограмм, кӧн тшӧтшыд пельӧс йывсянь лэдзӧм судта воча боксӧ юкӧ шӧри.

15. Вӧчны параллелограмм:

1) 2 см да 3 см кузя кык бок серти да на костса 110°-а пельӧс серти;

2) 2,1 см да 3,2 см кузя кык бок серти да 4,0 см кузя ӧти диагональ серти;

3) 6,0 см да 5,0 см кузя 2 диагональ серти да 4,5 см кузя ӧти бок серти;

4) 5 см да 4 см кузя 2 диагональ серти да на костса 135°-а пельӧс серти;

5) 2,0 см кузя подувтас, 1,5 см кузя судта да 3,2 см кузя диагональ серти.

Параллелограммъяс вылӧ разнӧй задачаяс.

16. Кык ӧткузя бока куимпельӧсалӧн боквывса бокыс 5 дм. Подувтас вывсянь^подувтасвывса чутсянь. — А.В./^ боквывса бокъясыслы параллельнӧя нуӧдӧма веськыд визьяс. Артавны артмӧм параллелограммлысь периметрсӧ.

17. Параллелограммын ёсь пельӧс йывсянь нуӧдӧм судтаяскостса пельӧс 1​5⁄11d ыджда. Определитны параллелограммлысь пельӧсъяссӧ.

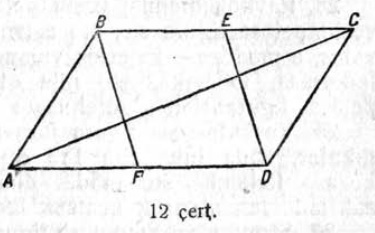
18. ABCD параллелограммын AD да BC параллельнӧй бокъяслысь E да F шӧръяссӧ ӧтлаалӧма D да B йывъяскӧд (12 чертёж). Докажитны, мый тайӧ веськыд визьясыс AC диагональсӧ юкӧны 3 ӧтыджда юкӧнъясӧ.

19. Кык ӧткузя бока куимпельӧсаын подувтасвывса произвольнӧй чутысь нуӧдӧма боквывса бокъясыслы параллельнӧй веськыд визьяс. Докажитны, мый артман параллелограммлӧн периметрыс оз зависит чут положенньӧсьыс да куимпельӧсаса боквывса бокъяс суммаыс ыджда.

Веськыднёльпельӧса.

20. Веськыднёльпельӧсаын диагональыс бокыскӧд вӧчӧ ⅖d ыджда пельӧс. Определитны диагональяскостса ичӧтджык бокыскӧд паныда пельӧссӧ.

21. Веськыднёльпельӧсаысь определитны бок да диагональ костса пельӧссӧ, коді сійӧ жӧ бок вылас подуласьысь диагональяскостса пельӧсысь ⅓d-ӧн ичӧтджык.

22. Эм-ӧ веськыднёльпельӧса пытшкын сэтшӧм чут, коді медым вӧлі: 1) ӧтылнаын став бокъяссяньыс? 2) став йывъяссяньыс?

23. Веськыднёльпельӧсаын диагональяслӧн вомӧнасянін чутсянь ичӧтджык бокӧдзыс ыджыдджык бокӧдз серти костыс 4 см ылынджык. Тайӧ веськыднёльпельӧсалӧн периметрыс 56 см. Определитны сылысь бокъяссӧ.

24. Веськыднёльпельӧсаын диагональясыс вомӧнасьӧны ⅔d пельӧс улын. Кыкнан диагональыслӧн да кыкнан ичӧтджык бокъясыслӧн суммаыс 3,6 м ыджда. Определитны диагональясыслысь кузьтаяссӧ.

25. ABCD — сетӧм веськыднёльпельӧса; M чут лоӧ BC боклӧн шӧр. Сетӧма, мый MA да MD визьяс мӧда-мӧдыслы перпендикулярнӧйӧсь да ABCD веськыднёльпельӧсалӧн периметрыс 24 м ыджда. Определитны сылысь бокъяссӧ.

26. Сетӧма веськыднёльпельӧса; йывсянь диагональ вылӧ лэдзӧм перпендикуляр веськыд пельӧссӧ юкӧ 2 пельӧ 3 : 1 отношенньӧын. Корсьны тайӧ перпендикулярыс да мӧд диагональ^вуджӧдӧмын вӧлі ӧшыбка: "диагональ" пыдди "бок". — А.В./^ костса пельӧссӧ.

27. Веськыд пельӧса куимпельӧсаӧ, кодлӧн быд катет 6 см ыджда, впишитӧма куимпельӧсакӧд ӧтувъя пельӧса веськыднёльпельӧса. Корсьны веськыднёльпельӧсалысь периметрсӧ.

28. Кык ӧткузя бока веськыд пельӧса куимпельӧсаӧ впишитӧма веськыднёльпельӧсаӧс сідз, мый сылӧн кык йыв куйлӧны гипотенуза вылын, а мӧд кыкыс — катетъяс вылын. Определитны веськыднёльпельӧсаяслысь бокъяссӧ, тӧдам кӧ, мый найӧ относитчӧны кыдз 5 : 2^ыджыдджыкыс куйлӧ гипотенуза вылын. — А.В./^, а куимпельӧсалӧн гипотенузаыс 45 см ыджда.

29. Веськыднёльпельӧсаын диагональ вылӧ йывсяньыс лэдзӧм перпендикуляр юкӧ сійӧс 1 : 3 отношенньӧын. Определитны диагональлысь кузьтасӧ, кор тӧдам, мый диагональяслӧн вомӧнассянін чутсяньыс ыджыдджык бокӧдзыс 2 м.

30. Вӧчны веськыднёльпельӧса:

1) 2,4 см кузя подувтас да 3,1 см кузя диагональ серти;

2) 4,2 см кузя диагональ да диагональяскостса 135° ыджда пельӧс серти;

3) 3,2 см кузя подувтас да диагональяскостса 120° ыджда пельӧс серти.

Веськыд визьсянь ӧтылнаӧ ылыстӧм чутъяслӧн геометрическӧй места.

31. Сетӧм AB веськыд визь вылысь корсьны сэтшӧм чут, кысянь мӧд сетӧм CD веськыдӧдз m ылна кост (m = 2 см).

32. Корсьны чут, кытчӧдз кык сетӧм чутсянь ӧтылнаын да сетӧм веськыд визьсянь a расстоянньӧ ылнаын (a = 6 см).

33. Сетӧм пельӧс пытшкын корсьны чут, кытчӧдз ӧти боксяньыс m расстоянньӧ, а мӧдсяньыс — n расстоянньӧ (m = 1 см, n = 2 см).

34. 1) Сетӧм пельӧс пытшкӧ вӧчӧма ӧти нима мӧд пельӧс, кодлӧн бокъясыс сетӧм пельӧс бокъясыслы параллельнӧйӧсь да насянь ӧтылнаынӧсь. Докажитны, мый кыкнан пельӧсыслӧн биссектрисаясыс совпадайтӧны.

2) Шӧри юкны пельӧс, кодлӧн йылыс чертёж вылӧ оз тӧр.

35. Сетӧма ёсь пельӧс да вундӧг. Колӧ тайӧ вундӧгсӧ пуктыны сетӧм пельӧс бокъяс костас сідз, медым сійӧ вӧлі ӧти бокыслы перпендикулярнӧй.

Ромб.

36. Ромбыд диагональяс пиысь ӧти диагональыс бок ыджда. Определитны ромблысь пельӧсъяссӧ.

37. Докажитны, мый:

1) быд параллелограмм, кодлӧн диагональясыс мӧда‐мӧдыслы перпендикулярнӧйӧсь, эм ромб;

2) быд параллелограмм, кодлӧн диагональыс пельӧссӧ юкӧ шӧри, эм ромб.

38. Ромблӧн бокыс диагональяскӧд вӧчӧ пельӧсъяс, кодъяслӧн разносьтыс 3⁄17d ыджда. Определитны ромблысь пельӧсъяссӧ.

39. Ромблӧн бокыс диагональясыскӧд вӧчӧ пельӧсъяс, кодъяс относитчӧны кыдз 5 : 4. Определитны ромблысь пельӧсъяссӧ.

40. Ромбын тшӧтшыд пельӧс йывсянь нуӧдӧм судта паныда боксӧ юкӧ шӧри. Определитны ромблысь пельӧсъяссӧ.

41. Ромблӧн периметрыс — 8 см, судтаыс — 1 см. Корсьны ромблысь тшӧтшыд пельӧссӧ.

42. Вӧчны ромб:

1) 2,7 см ыджда бок да 6,0 см ыджда диагональ серти;

2) 4 см да 3 см кузя кык диагональ серти;

3) 2,2 см ыджда судта да 4,2 см ыджда диагональ серти;

4) 70°-а пельӧс да тайӧ пельӧс пыр мунысь 3,7 см ыджда диагональ серти;

5) 5 см ыджда диагональ да сылы воча куйлысь 120° ыджда пельӧс серти.

Квадрат.

43. Вӧчны квадрат 3,8 см ыджда диагональ серти.

44. Сетӧма ABCD квадрат. Быд бок вылӧ пуктӧма ӧтыджда вундӧгъяс: AA₁ = BB₁ = CC₁ = DD₁. A₁, B₁, C₁, D₁ чутъяссӧ водзысь водзӧ ӧтлаалӧма. Докажитны, мый A₁B₁C₁D₁ — сідзжӧ квадрат.

45. Кык ӧткузя бока веськыд пельӧса куимпельӧсаӧ, кодлӧн быд катет 2 м кузя, впишитӧма квадрат. Квадратлӧн да куимпельӧсалӧн эм ӧти ӧтувъя пельӧс. Корсьны квадратлысь периметрсӧ.

46. Веськыд пельӧса куимпельӧсаын веськыд пельӧссӧ юкӧма шӧри, биссектрисалӧн гипотенузакӧд вомӧнассянін чутсьыс нуӧдӧма катетъяслы параллельнӧя веськыд визьяс. Докажитны, мый та ногӧн артмӧм нёльпельӧса эм квадрат.

47. Кык ӧткузя бока веськыд пельӧса куимпельӧсаӧ впишитӧма квадрат сідз, мый сылӧн кык йылыс гипотенуза вылын, а мӧд кыкыс — катетъяс вылын. Гипотенуза 3 м ыджда. Определитны квадратлысь боксӧ.

48. Сетӧма 1 м бока квадрат; сылӧн диагональыс лоӧ бокӧн мӧд квадратлы. Корсьны бӧръя квадратлысь диагональсӧ.

49. Квадратлӧн диагональыс 4 м. Сылӧн бокыс лоӧ диагональӧн мӧд квадратлы. Корсьны бӧръяыслысь боксӧ.

50. 1) Докажитны, мый веськыднёльпельӧса пельӧсъяслӧн биссектрисаясыс ас вомӧнассьӧмнас вӧчӧны квадрат.

2) Веськыднёльпельӧсалӧн бокъясыс 1 см да 3 см. Определитны пытшкӧс пельӧс биссектрисаясӧн артмӧм нёльпельӧсалысь диагональяссӧ.

51. Квадратӧ впишитӧма веськыднёльпельӧсаӧс сідз, мый быд квадрат бок вылын куйлӧ сылӧн ӧти йыв да бокъясыс сылӧн параллельнӧйӧсь квадрат диагональяслы. Определитны тайӧ веськыднёльпельӧсалысь бокъяссӧ, кор тӧдам, мый на пиысь ӧтиыс мӧдсьыс кык пӧв ыджыдджык да квадратлӧн диагональыс 12 м ыджда.

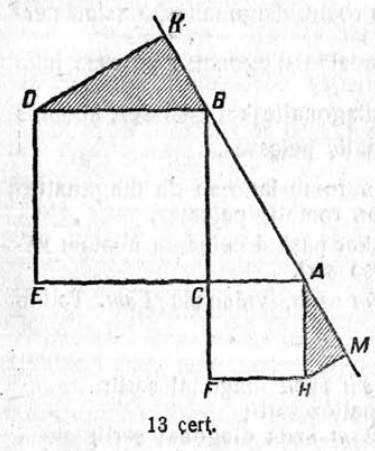
52. ABC веськыд пельӧса куимпельӧсаса катетъяс вылӧ вӧчӧма кык квадрат (13 чертёж). Тайӧ квадратъяс D да H йывъяссянь гипотенузасӧ нюжӧдӧм вылӧ лэдзӧма кык перпендикуляр: HM да DK. Докажитны, мый: 1) HM да DK перпендикуляръяслӧн суммаыс гипотенуза ыджда;

2) Сетӧм ABC куимпельӧсасӧ позьӧ составитны штрихуйтӧм кык куимпельӧсаясысь.

Куимпельӧсалӧн шӧр визь.

53. Стрӧпилӧяслӧн помъясыс мӧда-мӧдсяньыс 5 м сайын. Стрӧпилӧ джынъясӧ вӧчӧма йитӧд («ригель»). Определитны сылысь кузьтасӧ.

54. Куимпельӧсалӧн бокъясыс 8 см, 10 см, 12 см. Корсьны бокъяссӧ куимпельӧсалысь, кодлӧн йывъясыс сетӧм куимпельӧсаса бокъяс шӧрын.

55. Куимпельӧсалӧн периметрыс 12 см ыджда; бокъясыслысь шӧръяссӧ ӧтлаалӧма водзысь водзӧ. Корсьны артмӧм куимпельӧсалысь периметрсӧ.

56. Куимпельӧсалӧн бокъясыс относитчӧны кыдз 3 : 4 : 6. Став бокъясыслысь шӧръяссӧ ӧтлаалӧм бӧрын артман куимпельӧсалӧн периметрыс 5,2 м. Определитны сетӧм куимпельӧсалысь бокъяссӧ.

57. Сетӧма MN веськыд визь, сысянь ӧтар-мӧдар бокас сетӧма кык чут A да B, ӧтиыс 10 дм сайын, а мӧдыс 4 дм сайын веськыд визьсянь. Корсьны расстоянньӧсӧ AB вундӧг O шӧрсянь сетӧм веськыд визьӧдз.

58. Ӧткузя бокъяса^вуджӧдӧмын вӧлі ӧшыбка: "ӧткузя бокъяса" пыдди — "кык ӧткузя бока". — А.В./^ куимпельӧсалӧн судтаыс 6 дм ыджда. Корсьны сетӧм судталысь мӧд судта вылӧ проекциясӧ.

59. Тшӧтшыд пельӧса куимпельӧсаса тшӧтшыд пельӧс йыв пырыс ортсыті нуӧдӧма веськыд визь; тшӧтшыд пельӧс бокъяслӧн тайӧ веськыд визь вылӧ проекцияясыс 4 см да 2 см ыдждаӧсь. Определитны став медианаяслысь тайӧ жӧ веськыд визь вылӧ проекцияяссӧ.

60. Произвольнӧй пельӧс пытшкын босьтӧма M чут. M чут пыр нуӧдны веськыд визь сідз, медым сылӧн пельӧс бокъяскостса вундӧгыс M чутӧн юксис шӧри.

Трапеция.

61. ABCD трапецияын B йывсянь нуӧдӧма CD боклы AD ыджыдджык подувтаскӧд E чутын вомӧнассьытӧдз параллельнӧй веськыд. ABE куимпельӧсалӧн периметрыс 1 м ыджда, а ED-лӧн кузьтаыс 3 дм. Определитны трапециялысь периметрсӧ.

62. Трапециялысь боквывса боксӧ юкӧма 6 ӧтыджда юкӧнӧ, юкан чутъяссяньыс боквывса мӧд бок дінӧ нуӧдалӧма подувтасыслы параллельнӧй веськыд визьяс. Определитны тайӧ вундӧгъяслысь кузьтаяссӧ, трапециялӧн кӧ подувтасъясыс 10 см да 28 см ыдждаӧсь.

63. ABCD трапецияын (AD — ыджыд подувтас) сетӧма: AC ⟂ CD; AB = BC; ∠CAD = 2⁄7d. Определитны тайӧ трапециялысь пельӧсъяссӧ.

64. ABCD трапецияын (AD — ыджыдджык подувтас) AC диагональыс CD бокыслы перпендикулярнӧй да BAD пельӧссӧ юкӧ шӧри; ∠CDA = 60°; трапециялӧн периметрыс 2 м. Определитны AD.

65. Медым AD лоӧ ABCD трапецияын ыджыдджык улыс подувтасыс. Вермасны-ӧ A, B, C, D пельӧсъясыс мӧда-мӧдыськӧд относитчыны кыдз 2 : 5 : 6 : 3?

Трапециялӧн шӧр визь.

66. Трапециялӧн подувтасъясыс относитчӧны кыдз 7 : 3 да ӧтиыс мӧдсьыс 3,2 м кузьджык. Корсьны трапециялысь шӧр визьсӧ.

67. Трапециялӧн подувтасъясыс 2,4 м да 3 м. Тайӧ трапеция пытшкӧсті боквывса бокъяс костті подувтаслы параллельнӧя нуӧдӧма веськыд визь, кодлӧн кузьтаыс 2,8 м. Ӧтылнаын-ӧ тайӧ визьыс подувтасъяссянь, абу кӧ ӧтылнаын — кодсяньыс матынджык?

68. ABCD трапецияын AB боквывса бок E шӧрсьыс нуӧдӧма подувтасъяслы параллельнӧй веськыдӧс CD боккӧд F чутын вомӧнасьтӧдз; B йывсянь нуӧдӧма CD боклы параллельнӧй веськыдӧс AD ыджыд боккӧд G чутын вомӧнасьтӧдз. Определитны подувтасъясыслысь кузьтаяссӧ, EF-кӧ = 12 см, а AG = 1 см.

69. ABCD трапецияын AB боквывса бок E шӧрсянь нуӧдӧма боквывса CD боклы параллельнӧй веськыд визь AD ыджыдджык подувтаскӧд^вуджӧдӧмын ӧшыбка: "ыджыдджык подувтаскӧд" пыдди гижӧма "ыджда боккӧд". — А.В./^ G чутын вомӧнасьтӧдз. Определитны трапециялысь подувтасъяссӧ, AG-кӧ = 5 дм, а GD = 2,5 м.

70. Трапециялӧн шӧр визь 8 дм да диагональнас юксьӧ кык вундӧг вылӧ, кодъяс костын разносьтыс 2 дм ыджда. Определитны трапециялысь подувтасъяссӧ.

71. Корсьны трапецияса параллельнӧй бокъяс костысь отношенньӧ, шӧр визьыс кӧ диагональяснас юксьӧ 3 ӧтыджда юкӧнӧ.

Кык ӧткузя бока трапеция.

72. Докажитны, мый кык ӧткузя бока трапецияын подувтасъясбердса пельӧсъяс ӧтыдждаӧсь.

73. Сетӧм кык ӧткузя бока трапецияын боквывса бокыс шӧр визьыс ыджда, а периметрыс 24 м. Определитны боквывса боксӧ.

74. Определитны кык ӧткузя бока трапециялысь пельӧсъяссӧ, тӧдам кӧ, мый воча пельӧсъяслӧн разносьтыс 8⁄13d ыджда.

75. Кык ӧткузя бока трапецияын ичӧтджык подувтасыс боквывса бокыс ыджда, а диагональыс боквывса бокыслы перпендикулярнӧй. Определитны трапециялысь пельӧсъяссӧ.

76. ABCD — кык ӧткузя бока трапеция; AD — ыджыд подувтас. ACD да BAC куимпельӧсаяс периметръяс костын разносьт 6 дм; трапециялӧн шӧр визьыс 12 дм. Определитны подувтасъяссӧ.

77. Сетӧм кык ӧткузя бока трапецияын диагональыс ёсь пельӧссӧ юкӧ шӧри; тайӧ трапециялӧн периметрыс 4,5 м ыджда да ыджыдджык подувтасыс 1,5 м ыджда. Определитны ичӧтджык подувтассӧ.

78. Кык ӧткузя бока трапецияын тшӧтшыд пельӧс йывсянь нуӧдӧм судта юкӧ ыджыдджык подувтассӧ 6 см да 30 см кузя вундӧгъясӧ. Определитны трапециялысь подувтасъяссӧ.

79. ABCD — кык ӧткузя бока трапеция, AD — ыджыдджык подувтасыс; CE лоӧ AD вылӧ нуӧдӧм судта. Определитны подувтасъяссӧ, тӧдам кӧ, мый DE 1,25 м ыджда да трапециялӧн шӧр визьыс 2,75 м ыджда.

80. Кык ӧткузя бока трапецияын ыджыдджык подувтасыс 2,7 м, боквывса бокыс 1 м, на костса пельӧсыс 60°. Определитны ичӧтджык подувтассӧ.

81. Кык ӧткузя бока трапецияын ёсь пельӧсыс 45° ыджда, судтаыс h метр, шӧр визьыс m метр. Определитны трапециялысь подувтасъяссӧ.

82. Кык ӧткузя бока трапецияын судтаыс 10 см да диагональясыс мӧда-мӧдыслы перпендикулярнӧйӧсь. Корсьны шӧр визьсӧ.

Веськыд пельӧса трапеция.

83. Веськыд пельӧса трапецияыс диагональӧн юксьӧ кык куимпельӧсаӧ: a бока ӧткузя бокаӧ да веськыд пельӧса вылӧ. Определитны трапециялысь шӧр визьсӧ.

84. Веськыд пельӧса ABCD трапецияын ёсь ADC пельӧс = ½d да AD бокыс = a. CD бокса E шӧрас сувтӧдӧма сылы перпендикуляр, коді BA боклысь нюжӧдӧмсӧ вомӧналӧ F чутын. Определитны BF-лысь кузьтасӧ.

Трапецияӧс вӧчӧм.

83. Вӧчны трапеция:

1) 1,5 см да 2 см ыджда кык бок серти да 5 см да 2,3 см ыджда кык подувтас серти;

2) 4,8 см ыджда подувтас, 3,2 см ыджда судта, 4,2 см да 5 см кык диагональ серти;

3) 4 см ыджда подувтас серти, 2,4 см ыджда боквывса бок серти, на костса 72°-а пельӧс да 3 см ыджда мӧд боквывса бок серти.

86. Вӧчны трапеция:

1) нёльнан бок сертиыс (век-ӧ артмӧ задача?);

2) кык подувтас да кык диагональ серти (век-ӧ артмӧ задача?).

Параллелограммъяс да трапецияяс вылӧ смешаннӧй задачаяс.

87. Определитны сикассӧ нёльпельӧсалысь, кодлӧн йывъясыс куйлӧны сетӧм 1) произвольнӧй нёльпельӧса бокъяс шӧръясын, 2) параллелограмм бокъяс шӧръясын, 3) веськыднёльпельӧса бокъяс шӧръясын, 4) ромб бокъяс шӧръясын, 5) квадрат бокъяс шӧръясын, 6) трапеция бокъяс шӧръясын, 7) дельтоид бокъяс шӧръясын.

88. Нёльпельӧсаын диагональясыс 1 м да 8 дм кузяӧсь да вомӧнассьӧны 56°25′‐а пельӧс улын. Определитны бокъяссӧ да пельӧсъяссӧ артман нёльпельӧсалысь, коді артмӧ нёльпельӧсаса бок шӧръяссӧ ӧтлаалӧмӧн.

89. ABC куимпельӧсаын A пельӧслӧн биссектрисаыс BC боксӧ вомӧналӧ D чутын; D чутысь AC-лы параллельнӧя нуӧдӧм веськыд визь AB боксӧ вомӧналӧ E чутын; E чутысь BC-лы параллельнӧя нуӧдӧм веськыд визь AC боксӧ вомӧналӧ F чутын. Докажитны, мый EA = FC.

90. 1) Кык ӧткузя бока куимпельӧса подувтас вылын босьтӧма чут. Докажитны, мый тайӧ чутсянь боквывса кыкнан бокъясӧдзыс расстоянньӧяслӧн суммаыс боквывса судтаыс^вуджӧдӧмын ӧшыбка: "судтаыс" пыдди гижӧма "бокыс". — А.В./^ ыджда.

2) Кык ӧткузя бока куимпельӧса подувтас нюжӧдӧм вылын босьтӧма чут. Докажитны, мый тайӧ чутсянь боквывса бокъясӧдзыс расстоянньӧяслӧн разносьтыс бокса судта ыджда.

Центральнӧй симметрия.

91. Петкӧдлыны бергӧдӧмлысь медічӧт пельӧссӧ, кор ӧтлаасьӧ ачыс аскӧдыс 1) квадрат, 2) ромб, 3) веськыднёльпельӧса, 4) сӧветскӧй звезда.

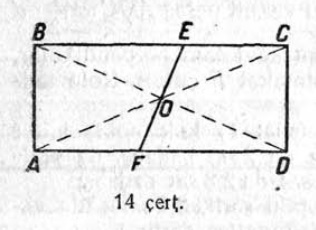
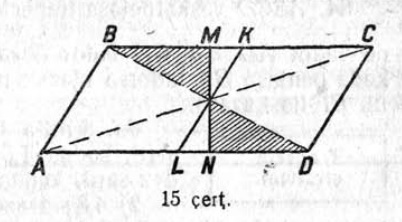
92. Докажитны, мый веськыднёльпельӧсаса диагональяс вомӧнассянін O чут пыр мунысь веськыд визь юкӧ веськыднёльпельӧсасӧ кык центрально-симметрическӧй нёльпельӧса вылӧ (14 чертёж).

93. Видлавны чертёж (15 чертёж) да докажитны, мый M да N, K да L чутъяс центрально-симметричнӧйӧсь, либӧ мӧд ног кӧ, шӧр чутсянь ӧтылнаынӧсь. Кутшӧм построенньӧӧн артмӧны параллелограммын центрально-симметричнӧй чутъяс?

6 §. Кытшвизь.

Кытшвизь, сылӧн положенньӧыс. Диаметр, хорда, сыӧдз шӧр чутсянь расстоянньӧ. Вомӧналысь.

1. 120°-а ABC пельӧс бокъяс вылӧ пукталӧма вундӧгъяс AB = BC = 4 см. A, B, C чутъяс пыр нуӧдны кытшвизь да корсьны, ыджыд-ӧ сылӧн радиусыс.

2. Корсьны сетӧм радиуса да сетӧм чут пыр мунысь кытшвизьяс шӧр чутъяслысь геометрическӧй места.

3. Нуӧдны кытшвизь, коді медым муніс 2 сетӧм чут пыр да кодлӧн шӧр чутыс медым вӧлі сетӧм веськыд визь вылын.

4. Вӧчны кытшвизь, коді медым муніс 2 сетӧм чут A да B пыр да медым кругса радиус да AB хорда костын артмис 30°-а пельӧс.

5. 1) Кытшвизьлӧн радиусыс 10 см; сетӧм чут шӧр чутсяньыс 15 см сайын. Корсьны сысянь кытшвизьӧдз медыджыд да медічӧт расстоянньӧяссӧ.

2) Кытшвизьлӧн радиусыс 10 см; сетӧм чут шӧр чутсяньыс 3 см сайын. Корсьны сыӧдз кытшвизьсянь медыджыд да медічӧт расстоянньӧяссӧ.

6. Сетӧм чутӧдз кытшвизьсянь медматыс расстоянньӧ a ыджда, а медылыс — b ыджда. Корсьны радиуссӧ (2 случай).

7. Докажитны, мый кык кытшвизь костса медматыс расстоянньӧ эм шӧр чутъяс визьлӧн вундӧг, коді лоӧ кытшвизьяс костын. Кытшвизьяс куйлӧны мӧда-мӧдсьыс ортсыын.

8. Сетӧм кытшвизьвывса чутысь нуӧдӧма диаметр да радиус ыджда хорда. Корсьны на костса пельӧссӧ.

9. Сетӧм кытшвизьвывса чутысь нуӧдӧма радиус ыджда кык хорда. Корсьны на костса пельӧссӧ.

10. Кругын сетӧма мӧда‐мӧдыслы перпендикулярнӧй кык хорда; на пиысь кыкнаныс мӧда-мӧдсӧ юкӧны 3 см да 7 см ыджда вундӧгъясӧ. Корсьны быд хордасянь шӧр чутӧдз расстоянньӧяссӧ.

11. Кругын шӧр чутсянь 1 см сайын сетӧма мӧда-мӧдыслы перпендикулярнӧй кык хорда; кыкнаныс на пиысь 6 см кузяӧсь. Корсьны, кутшӧм юкӧнъясӧ юксьӧ ӧтиыс мӧднас.

12. R радиуса кругын сетӧма мӧда-мӧдыслы 2 перпендикулярнӧй диаметр; кытшвизьвывса произвольнӧй чутӧс проектируйтӧма тайӧ перпендикуляръяс вылӧ. Корсьны чут проекцияяскостса расстоянньӧсӧ.

13. Хорда диаметрӧс вомӧналӧ 30°-а пельӧс улын да юкӧ сійӧс 2 см да 6 см ыджда вундӧгъясӧ. Корсьны шӧр чутсянь хордаӧдз расстоянньӧ.

14. Кытшвизьвывса чутсянь нуӧдӧма мӧда-мӧдыслы перпендикулярнӧй 2 хорда, кодъясӧдз шӧр чутсянь 6 см да 10 см. Определитны налысь кузьтаяссӧ.

15. Диаметр помъясӧдз касательнӧйсянь 1,6 м да 0,6 м. Определитны диаметрлысь кузьтасӧ.

16. O шӧр чута кругын нуӧдӧма AB хорда да нюжӧдӧма сійӧс радиус ыджда BC вундӧг ылнаӧ. C чут да O шӧр чут пыр нуӧдӧма CD вомӧналысьӧс (D — кытшвизьыскӧд вомӧнасян чут, коді куйлӧ CO вундӧг сайын). Докажитны, мый AOD пельӧс куим пӧв ыджыдджык ACD пельӧсысь.

17. 1) Сетӧма 2 см ыджда радиуса круг. Нуӧдны сы пытшкын 1,5 см кузя хорда. Определённӧй-ӧ тайӧ задачаыс? Кымын решенньӧ вермас лоны задачалӧн, сетӧм кузьтаа хордалы кӧ ковмас мунны кытшвизьвывса сетӧм чут пыр?

2) Петкӧдлыны, мый сетӧм кузьтаа хордаяслӧн, кодъясӧс нуӧдӧма сетӧм кытшвизьын, шӧръясыс куйлӧны кутшӧмкӧ мӧд кытшвизь вылын.

18. 1) Докажитны, мый круг пытшкын босьтӧм A чут пыр мунысь став хорда пиысь медічӧтӧн лоӧ сійӧ, коді A чут пыр мунысь диаметрлы перпендикулярнӧй.

2) Кругын сетӧм чут пыр нуӧдны хорда сідз, медым сійӧ тайӧ чутӧн юксис шӧри.

19. Пельӧс бок вылын сетӧм чутсянь опишитны кытшвизь сідз, медым сійӧ пельӧс мӧд бок вылысь вундіс сетӧм кузьтаа хорда.

20. Сетӧм кругын нуӧдӧма мӧда-мӧдыслы параллельнӧй 2 ӧтыджда хорда, кодъяс костын расстоянньӧыс сетӧм круг радиусыс ыджда. Корсьны хордаяслысь помъяссӧ ӧтлаалысь веськыд визьяс костын артман ёсь пельӧссӧ.

Касательнӧй. Веськыд визьяслӧн да кытшвизьяслӧн сопряженньӧ.

21. 1) Ортсыса чутсянь 10 см ыджда радиуса круг бердӧ нуӧдӧма мӧда-мӧдыслы 2 перпендикулярнӧй касательнӧй. Корсьны быд касательнӧйлысь кузьтасӧ.

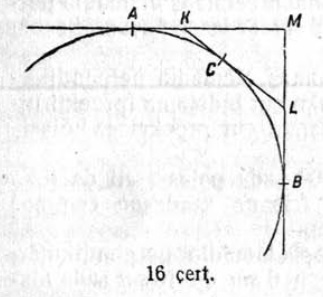
2) Сетӧма круг, кодлӧн радиусыс R = 1 дм; ортсыса M чутсянь сы бердӧ нуӧдӧма мӧда-мӧдыслы 2 перпендикулярнӧй касательнӧй: MA да MB (16 чертёж). AB дуга вылын A да B чутъяс костын босьтӧма произвольнӧй C чут да сы пыр нуӧдӧма круглы коймӧд KL касательнӧй, коді MA да MB касательнӧйясысь вундӧ KLM куимпельӧса. Корсьны тайӧ куимпельӧсалысь периметрсӧ.

22. Сетӧма R радиуса круг нёльӧд юкӧн ыджда сектор. Сійӧ дуга шӧрӧдыс нуӧдӧма касательнӧй, дорса радиусъяссӧ нюжӧдӧмыскӧд вомӧнассьытӧдз. Определитны касательнӧйлысь кузьтасӧ.

23. Веськыд пельӧсӧ впишитӧма круг; касайтчан чутъяссӧ ӧтлаалысь хордаыс 2 дм ыджда. Корсьны тайӧ хордаӧдз шӧр чутсянь расстоянньӧсӧ.

24. AB да AC — ӧти кытшвизь дінӧ касательнӧйяс; ∠BAC = 60°; BAC чегласьӧм визь 1 м кузя. Определитны B да C чутъяс костса расстоянньӧсӧ.

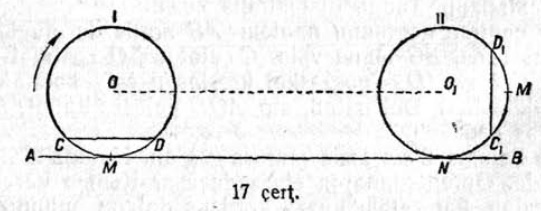
25. Круглӧн кытшвизьыс 18,84 см кузя; круг гӧгыльтчӧ AB веськыд визь кузя (17 чертёж). Уна-ӧ мунас круглӧн шӧр чутыс, кор кругыс І положенньӧысь вуджас ІІ положенньӧӧ? І положенньӧын CD хорда ∥ AB, а ІІ положенньӧ дырйи хорда C₁D₁ ⊥ AB.

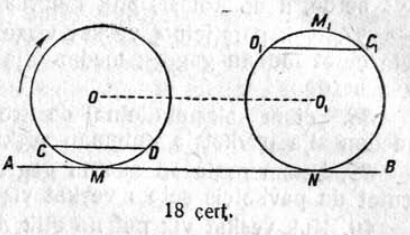
26. Круглӧн кытшвизьыс 18,84 см кузя; круг гӧгыльтчӧ AB веськыд визь кузя (18 чертёж). Уна-ӧ мунас сылӧн O шӧр чутыс, кор сылӧн хордаыс первоначальнӧй CD ∥ AB положенньӧсьыс лоас C₁D₁ ∥ AB положенньӧын?

27. Кык круглӧн радиусыс 2 см да 4 см ыдждаӧсь; налӧн ӧтувъя пытшкӧс касательнӧйясыс мӧда-мӧдыслы перпендикулярнӧйӧсь. Корсьны кыкнаныслысь кузьтасӧ.

28. Сетӧма кык круг; налӧн ӧтувъя пытшкӧс касательнӧйясыс мӧда-мӧдыслы перпендикулярнӧйӧсь; касайтчан чутъяссӧ ӧтлаалысь хордаяс 3 см да 5 см ыдждаӧсь. Определитны шӧр чутъяскостса расстоянньӧсӧ.

29. Сетӧма R да r радиусъяса 2 круг; ӧтиыс мӧдсьыс ортсын; на бердӧ нуӧдӧма 2 ӧтувъя ортсыса касательнӧйяс, кодъяслӧн нюжӧдӧмъясыс вӧчӧны веськыд пельӧс. Корсьны налысь кузьтасӧ (касайтчан чутъяс костсӧ).

30. Сетӧма 30° ыджда пельӧс. 2,5 см кузя радиусӧн вӧчны кытшвизь сідз, медым сійӧ касайтчис пельӧс ӧти бокас да шӧр чутыс вӧлі пельӧс мӧд бок вылас. Корсьны пельӧс йывсянь шӧр чутӧдз расстоянньӧ.

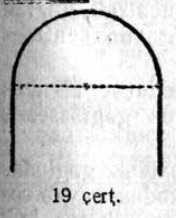
31. Чертитны кытшвизь джынйӧн сопрягайтчан кык параллельнӧй веськыд визьысь выпуклӧй фигура. Архитектураын татшӧм фигура, кор сійӧ горизонтальнӧй, шусьӧ «валикӧн», а кор вертикальнӧй — «аркадаӧн» (19 чертёж).

32. Кык непараллельнӧй веськыд визьӧс ӧтлаавны найӧс сопрягайтысь дугаӧн. Видзӧдлыны 3 случай: 1) кор ӧтлаасян (касайтчан) чутъяссӧ да дуга радиуссӧ абу сетӧма; 2) кор сетӧма сӧмын дугаыслысь радиуссӧ; 3) кор сетӧма ӧтлаасян чутсӧ, а радиуссӧ абу сетӧма (веськыд визьяслӧн дугаяскӧд татшӧм ӧтлаассьӧмъяс вылӧ примеръясӧн лоӧны кӧрт туйлӧн «закругленньӧяс»).

33. Корсьны сетӧм радиусӧн вӧчӧм да сетӧм веськыд визь бердӧ касайтчысь кытшвизьяс шӧр чутъяслысь геометрическӧй места.

34. Сетӧм радиусӧн вӧчны кытшвизь, коді медым касайтчис сетӧм веськыд визьӧ сы вылын сетӧм чутын.

35. Вӧчны кытшвизь, коді медым муніс сетӧм A чут пыр да касайтчис сетӧм веськыд визьӧ сы вылын сетӧм B чутын.

36. Вӧчны кытшвизь, коді медым касайтчис сетӧм пельӧс бокъясӧ да на пытшкысь ӧтиас сетӧм чутын.

37. Кык параллельнӧй веськыд визь костын сетӧма чут; нуӧдны кытшвизь, коді медым муніс тайӧ чут пыр да касайтчис сетӧм веськыдъясӧ.

38. Сетӧма 2 параллельнӧй да вундысь. Нуӧдны куимнан веськыд визяс касайтчан кытшвизь.

39. Сетӧм радиусӧн нуӧдны сетӧм чут пыр мунысь да сетӧм веськыд визьӧ касайтчысь кытшвизь.

40. Кык веськыд визь петӧны ӧти сійӧ жӧ M чутысь да касайтчӧны кытшвизь A да B чутъясын. Нуӧдӧма OB радиус да сійӧс нюжӧдӧма B чут сайӧ BC = OB расстоянньӧ ылнаӧ. Докажитны, мый ∠AMC = 3∠BMC.

Кык кытшвизьлӧн относительнӧй положенньӧ.

41. Кутшӧм кык кытшвизьлӧн относительнӧй положенньӧыс, кор:

1) шӧр чутъяскостса расстоянньӧыс 10 см, а радиусъясыс 8 см да 2 см;

2) шӧр чутъяскостса расстоянньӧыс 4 см, а радиусъясыс 11 см да 7 см;

3) шӧр чутъяскостса расстоянньӧыс 12 см, а радиусъясыс 5 см да 3 см.

42. Кык кытшвизьлӧн радиусъясыс относитчӧны кыдз 5 : 3, пытшкӧс касанньӧ дырйи шӧр чутъяскостса расстоянньӧыс 6 дм ыджда. Тӧдмавны тайӧ жӧ кытшвизьяслысь относительнӧй положенньӧсӧ, кор шӧр чутъяскостса расстоянньӧыс лоӧ 1) 24 дм, 2) 5 дм, 3) 28 дм, 4) 20 дм.

43. Сетӧма 2 круг — ӧтиыс мӧдыс пытшкын; найӧ шӧр чутъяс пыр нуӧдӧма ыджыдджык кругыслысь диаметр, коді ичӧтджык кытшвизьнас юксьӧ 3 вундӧг вылӧ: 5 см, 8 см, 1 см. Корсьны шӧр чутъяскостса расстоянньӧсӧ.

44. Кык концентрическӧй кытшвизьяскостса медічӧт расстоянньӧыс = 2 см, а медыджыдыс = 16 см. Определитны тайӧ кытшвизьяслысь радиусъяссӧ.

45. Сетӧма 2 концентрическӧй круг; ыджыдджык кругас сетӧма мӧда-мӧдыслы перпендикулярнӧй 2 хорда, кодъяс касайтчӧны ичӧтджыкас; быд хорда мӧднас юксьӧ 2 пельӧ: 3 см да 7 см. Корсьны ичӧтджык круглысь радиуссӧ.

46. Кык концентрическӧй кытшвизьлӧн радиусъясыс относитчӧны кыдз 7 : 4, кольчаыслӧн пасьтаыс 12 см ыджда. Определитны ичӧтджык кытшвизьлысь радиуссӧ.

47. Кык концентрическӧй круг кӧ вомӧнавны вундысьӧн (вомӧналысьӧн), вундысьлӧн кытшвизьяс костын куйлысь юкӧнъясыс ӧтыдждаӧсь. Докажитны.

48. Ӧти кытшвизь мӧдыс пытшкын; налӧн радиусъясыс 28 см да 12 см ыдждаӧсь, а медматыс расстоянньӧ на костын 10 см. Определитны шӧр чутъяскостса расстоянньӧсӧ.

49. 1) R радиуса куим кытшвизь касайтчӧны мӧда-мӧдас ортсысянь. Определитны бокъяссӧ да пельӧсъяссӧ куимпельӧсалысь, кодлӧн йывъясыс — касанньӧ чутъяс.

2) Сетӧм кругӧ впишитны 3 ӧтыджда круг сідз, медым найӧ касайтчисны сетӧм кругас да гозйӧн-гозйӧн мӧда‐мӧдыскӧд.

50. Кык ӧтыджда круг пытшкӧссянь касайтчӧны коймӧдӧ да касайтчӧны мӧда-мӧдас. 3 шӧр чутсӧ кӧ ӧтлаавны, лоӧ куимпельӧса 18 см ыджда периметрӧн. Определитны ыджыдджык кругыслысь радиуссӧ.

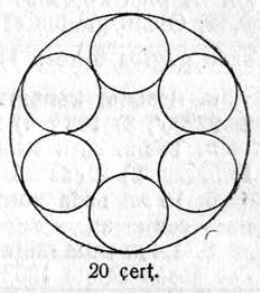
51. 3 дм радиуса сетӧм кругӧ впишитӧма 6 ӧтыджда круг (20 чертёж), кодъяс пиысь быд ӧти касайтчӧ сетӧм кругас да 2 ас кодяс. Корсьны налысь диаметръяссӧ. Вӧчны чертёж.

52. 1 дм радиуса круг гӧгӧр ортсысяньыс нуӧдӧма 6 ӧтыджда круг, кодъяс пиысь быд ӧти касайтчӧ сетӧм кругас да 2 ас кодяс. Корсьны налысь радиусъяссӧ. Вӧчны чертёж.

Кытшвизьясӧс да дугаясӧс вӧчӧм.

53. 1) Корсьны кытшвизьяс шӧр чутъяслысь геометрическӧй места, кодъяс касайтчӧны сетӧм кытшвизь бердӧ сы вылын сетӧм чутын.

2) Нуӧдны кытшвизь сідз, медым сійӧ муніс сетӧм чут пыр да касайтчис сетӧм кытшвизьӧ сы вылын сетӧм чутын.

54. 1) Корсьны кытшвизьяс шӧр чутъяслысь геометрическӧй места, кодъясӧс вӧчӧма сетӧм радиусӧн да касайтчӧны сетӧм кытшвизь бердӧ (2 случай: ортсыса касанньӧ да пытшкӧс касанньӧ).

2) Сетӧм радиусӧн нуӧдны кытшвизь, коді медым касайтчис сетӧм веськыдӧ да сетӧм кругӧ.

55. Ӧтлаавны сетӧм веськыдӧс да сетӧм дугаӧс сетӧм радиуса сопрягайтысь дугаӧн; ӧтлаасян (касайтчан) чутъяссӧ абу сетӧма.

56. Ӧтлаавны 2 сетӧм дуга сетӧм радиуса сопрягайтысь дугаӧн; касайтчан чутъяссӧ абу сетӧма.

57. Нуӧдны кытшвизь, коді медым касайтчис кык сетӧм параллельнӧй веськыд визьясӧ да на костын куйлысь кругӧ.

58. Кык кытшвизь вомӧнассянін чут пыр нуӧдны вомӧналысьӧс сідз, медым сылӧн кытшвизьяс пытшкӧсса юкӧныс вӧлі сетӧм кузьта ыджда.

7 §. Дугаясӧн пельӧсъясӧс мурталӧм.

Центральнӧй пельӧс.

1. 1) Зубчатӧй передачаын ыджыд кӧлесалӧн 72 пинь. Кымын градус дугаын, кодӧс занимайтӧ ӧти пинь коласыскӧд тшӧтш?

2) Зубчатӧй передачалӧн ичӧт кӧлесаын 24 пинь. Кымын градус дугаын, кодӧс занимайтӧ ӧти пинь коластыскӧд (впадинаыскӧд) тшӧтш?

3) Кымынӧд пай бергӧдчӧмыслысь вӧчас 72 пиня кӧлеса, кор сыкӧд йитӧм 24 пиня кӧлесаыс вӧчас быдса бергӧдчӧм?

2. Петкӧдлыны градусъясӧн, минутъясӧн, секундъясӧн кытшвизьлысь со кутшӧм юкӧнъяс: 1) 1⁄72; 2) 1⁄81; 3) 0,001; 4) 1⁄14; 5) 5⁄11.

3. Корсьны, кутшӧм юкӧн кытшвизьлысь составляйтӧны дугаяс: 1) 15°; 2) 22°30′; 3) 108°; 4) 24′; 5) 18″; 6) 18°45′; 7) 2°0′30″; 8) 10′40″.

4. Определитны часі вылысь стрелкаяскостса пельӧссӧ, кор часі петкӧдлӧ: 1) 5 час; 2) 3 час 25 мин.; 3) 4 час 50 мин.

5. 16 см ыджда хорда стягивайтӧ 90°-а дуга. Определитны сысянь шӧр чутӧдз расстоянньӧ.

6. 1,4 м радиуса кытшвизьын определитны шӧр чутсянь 120°-а дугаӧс стягивайтысь хордаӧдз расстоянньӧ.

7. Кык радиус костын 102°0′37″ пельӧс. Определитны тайӧ радиусъяс помъяс пыр нуӧдӧм касательнӧйяскостса пельӧс.

8. AB дугаын 73°27′; сійӧ B помысь нуӧдӧма касательнӧйӧс OA радиус нюжӧдӧмкӧд C чутын вомӧнассьытӧдз. Определитны ∠ACB.

Вписаннӧй пельӧс.

9. Кымын градус да минут дугаын, помса радиусыс кӧ хордаыскӧд вӧчӧ 37°23′ пельӧс?

10. Дугаын 117°23′. Определитны пельӧс, коді артмӧ хорда да помса радиуссӧ нюжӧдӧм костын.

11. ABC — вундысь; BD — хорда; ‿BD-ын 43°; ‿BDC-ын 213°41′. Определитны ∠ABD.

12. Артавны кытшвизьлысь 17⁄32 ыджда дугаӧ впишитӧм пельӧс.

13. Кымын градус да минут дугаын, код пытшкын 37°21′ пельӧс?

14. Дугаын 84°52′. Кутшӧм пельӧс улын тыдалӧ тайӧ дугавывса чутъяссянь аслас хордаыс?

15. Хорда юкӧ кытшвизьӧс 5 : 11 отношенньӧын. Определитны вписаннӧй пельӧсъяслысь величинаяссӧ, кодъяс мыджсьӧны тайӧ хорда вылӧ.

16. AB да AC — кык хорда; ‿AB-ын 110°23′; ‿AC-ын 38°. Определитны ∠BAC (Кык ӧтвет).

17. AB хорда юкӧ кытшвизьӧс кык дуга вылӧ, кодъяс пиысь ичӧтджыкыс 130° ыджда, а ыджыдджыкыс AC хордаӧн юксьӧ 31 : 15 отношенньӧын (A-сянь заводитӧмӧн). Определитны ∠BAC.

18. AB да AC хордаяс куйлӧны шӧр чутсянь разнӧй бокъясын да на костса пельӧсыс 72°30′ ыджда; ‿AB : ‿AC = 19 : 24. Определитны тайӧ дугаяссӧ.

19. Кытшвизьӧс юкӧма 7 : 11 : 6 отношенньӧын да юкан чутъяссӧ мӧда-мӧдыскӧд ӧтлаалӧма. Определитны артман куимпельӧсалысь пельӧсъяссӧ.

20. Определитны, кымын градус дугаын, перпендикулярыс кӧ, кодӧс нуӧдӧма хордасянь сійӧ помысь, юкӧ кытшвизьӧдз содтысь дугаӧс 5 : 2 отношенньӧын.

21. Куимпельӧсаын кӧ медиана соответствуйтысь бок сертиыс джын ыджда, тайӧ боклы воча пельӧсыс лоӧ веськыд. Докажитны тайӧтор отсасьысь кытшвизь отсӧгӧн.

22. A да B чутъясӧс ӧтлаалӧма кык дугаӧн, кодъяслӧн выпуклосьтъясыс видзӧдӧны разнӧй бокъяслань: ‿ACB-ын 117°23′ да ‿ADB-ын 42°37′; налысь C да D шӧръяссӧ ӧтлаалӧма A‐кӧд. Определитны ∠CAD.

23. Докажитны, мый кругӧ впишитӧм быд трапеция — кык ӧткузя бока.

24. AMB сегментӧ впишитӧма ACDB трапецияӧс, кодлӧн AC бок = CD да ∠CAB = 51°20′. Кымын градус AMB дугаын?

25. AB — диаметр; C, D, E — чутъяс, кодъяс куйлӧны ACDEB кытшвизь джын вылын. AB диаметр вылын босьтӧма: F чут сідз, мый ∠CFA = ∠DFB, да G чут сідз, мый ∠DGA = ∠EGB. ‿AC-ын 60° да ‿BE-ын 20°. Определитны ∠FDG.

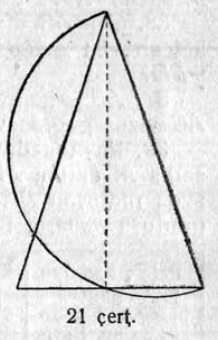
26. Кык ӧткузя бока куимпельӧсаын йывбердса пельӧсыс 40° ыджда. Боквывса бокъяс письыс ӧтиыс — кытшвизь джынлӧн диаметр. Кытшвизь джынйыс мукӧд кык бокнас юксьӧ куим юкӧн вылӧ (21ʼ чертёж). Корсьны сійӧ юкӧнъяссӧ.

27. Ӧткузя бокъяса куимпельӧсаын подувтасыс — кытшвизьлӧн диаметр. Кутшӧм юкӧнъясӧ кытшвизьнас юксьӧны куимпельӧсалӧн бокъясыс да кутшӧм юкӧнъясӧ кытшвизь джын юксьӧ куимпельӧсаса бокъяснас?

28. Кыдз пасйыны циркультӧг, сӧмын чертёжнӧй куимпельӧсаӧн пӧльзуйтчӧмӧн, кытшвизьлысь чутъяссӧ?

29. Вӧчны веськыд пельӧса куимпельӧсаӧс, кор сетӧма гипотенуза C = 5 см да сы вылӧ веськыд пельӧс йывсянь лэдзӧм судта, кодлӧн кузьтаыс 2 см.

30. Вӧчны веськыд пельӧса куимпельӧсаӧс, кор сетӧма 3,5 см кузя гипотенуза да ӧти катетыслӧн гипотенуза вылӧ 2,9 см ыджда проекция.

31. Корсьны ӧти чутын вомӧнассьысь став хорда шӧръяслысь геометрическӧй места. Видлавны кык случай: 1) чутыс кытшвизь вылын; 2) чутыс кытшвизь пытшкын.

32. Кык кытшвизь касайтчан чут пыр нуӧдӧма вундысьӧс. Артмӧм хордаяс помъяс пыр нуӧдӧм радиусъяс да касательнӧйяс параллельнӧйӧсь. Докажитны.

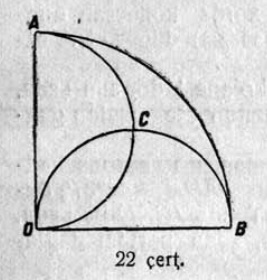
33. AOB круг нёльӧд юкӧнса OA да OB радиусъяс вылӧ (кыдз диаметръяс вылӧ) вӧчӧма кытшвизь джынъяс: ACO да OCB (22 чертёж). Докажитны, мый 1) OC веськыд визь юкӧ AOB пельӧссӧ шӧри; 2) A, C да B чутъяс куйлӧны ӧти веськыд визь вылын; 3) AC, CO, CB дугаяс ӧтыдждаӧсь.

34. Кытшвизьӧс 3 : 5 отношенньӧын юкысь хорда пом пыр нуӧдӧма касательнӧйӧс. Определитны хорда да касательнӧй костысь ёсь пельӧссӧ.

35. AB да AC — ӧтыджда хордаяс; MAN — касательнӧй; ‿BC-ын 213°42′. Определитны MAB да NAC пельӧсъяс.

36. C лоӧ AB диаметрӧс нюжӧдӧм вылын чут; CD — касательньӧй; ∠ADC = 114°25′. Кымын градус да минут BD дугаын?

37. AB — кытшвизьлӧн диаметр; BC — касательнӧй. AC вундысьыс кытшвизь вылын D чутын юксьӧ шӧри. Определитны ∠DAB.

38. M чут лоӧ ABC кык ӧткузя бока куимпельӧсаын BD судталӧн шӧрыс; тайӧ M чутыс буретш ладмӧ шӧр чутӧн дугалы, кодӧс нуӧдӧма BA да BC бокъяс костӧд MD радиусӧн. Определитны тайӧ дугалысь величинасӧ, кор тӧдам, мый ∠BAC = 62°17′.

Круг пытшкын да круг сайын йыла пельӧсъяс. Описаннӧй пельӧс.

39. Кытшвизьӧс юкӧма A, B, C да D чутъясӧн сідз, мый ‿AB : ‿BC : ‿CD : ‿DA = 2 : 3 : 5 : 6. Нуӧдӧма M чутын вомӧнасьысь AC да BD хордаяс. Определитны ∠AMB.

40. AB диаметр да CD хорда вомӧнасьӧны M чутын; ∠CMB = 73°; ‿BC-ын 110°. Кымын градус ‿BD-ын?

41. AB да CD хордаяс вомӧнасьӧны M чутын; ∠AMC = 40°; ‿AD ‿CB-ысь 20°54′-ӧн ыджыдджык. Определитны ‿AD.

42. m°-а ‿AB помъясысь нуӧдӧма AC да BD хордаяс сідз, мый найӧ вомӧнасьӧмӧн артман ∠DMC CD дугаӧ впишитӧм ∠DNC ыджда. Определитны тайӧ дугасӧ.

43. ABCD нёльпельӧсаын B да D пельӧсъяс веськыдӧсь; AC диагональ AB боккӧд вӧчӧ 40°-а пельӧс, а AD боккӧд вӧчӧ 30°-а пельӧс. Определитны AC да BD костса ёсь пельӧссӧ.

44. Кытшвизьӧс A, B, C, D чутъясӧн юкӧма сідз, мый ‿AB : ‿BC : ‿CD : ‿DA = 3 : 2 : 13 : 7. AD да BC хордаяссӧ нюжӧдӧма M чутын вомӧнассьытӧдз. Определитны ∠AMB.

45. Сетӧма хордаа да касательнӧй визя кытшвизьӧс, касанньӧ чутыс куйлӧ кык дугаяс пиысь ичӧтджыкыс вылын, кодъясӧс стягивайтӧ хорда. Касательнӧй вылысь корсьны чут, кысянь медым хорда вӧлі тыдалӧ медыджыд пельӧс улын.

46. ABC вундысь вундӧ 112°-а ‿BC; AD касательнӧй касанньӧ D чутнас юкӧ тайӧ дугасӧ 7 : 9 отношенньӧын. Определитны ∠BAD.

Индӧд (водзӧ локтан некымын задачаяслы). Описаннӧй пельӧсӧс определитігӧн колӧ тӧдны, мый кык касательнӧй костса пельӧс лоӧ касанньӧ чутъясӧ нуӧдӧм радиусъяскостса пельӧс дінӧ 180°‐ӧдз содтӧдӧн.

47. 200°30′ ыджда дуга помъяссянь нуӧдӧма касательнӧйясӧс мӧда-мӧдыскӧд вомӧнассьытӧдз. Определитны на костса пельӧссӧ.

48. Описаннӧй пельӧсын 73°25′. Определитны дугаяс^вуджӧдӧмын ӧшыбка, гижӧма "пельӧсъяссӧ". — А.В./^, кодъяс сы бокъяс костын.

49. Хорда кытшвизьӧс юкӧ 11 : 16 отношенньӧын. Тайӧ хорда помъяс пыр нуӧдӧма касательнӧйясӧс. Определитны на костын артман пельӧссӧ.

50. Сетӧм кытшвизь пытшкын эм мӧд кытшвизь (23 чертёж). Ыджыдджык кытшвизьыслӧн ABC да ADE хордаяс B да D чутъясын касайтчӧны ичӧтджык кытшвизьӧ; BMD — касанньӧ чутъяс костас ичӧтджык дугаыс; CNE — хордаяс помъяскостса дуга; ‿BMD-ын 130°. Определитны ‿CNE.

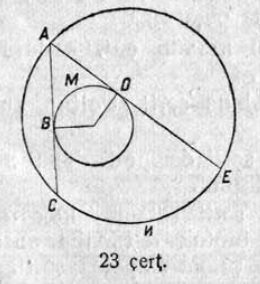
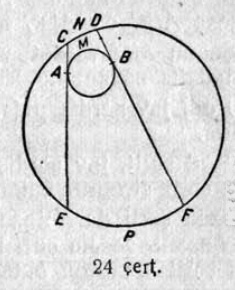
51. Сетӧм кытшвизь пытшкын эм мӧд кытшвизь. Ыджыдджык кытшвизьыслӧн CAE да DBF хордаясыс (оз вомӧнассьыны) A да B чутъясын касайтчӧны ичӧтджык кытшвизяс; AMB — касанньӧ чутъяс костын ичӧтджык дугаыс; CND да EPF — хордаяс помъяскостса дугаяс; ‿AMB-ын 154°, а ‿EPF-ын — 70°. Кымын градус ‿CND-ын?

52. Кытшвизьӧс юкӧма 5 : 9 : 10 отношенньӧын да юкан чутъясыс пыр нуӧдӧма касательнӧйясӧс. Определитны медыджыд пельӧссӧ артмӧм куимпельӧсаысь.

53. AB да AC — кык хорда; найӧ вӧчӧны 74°24′ ыджда BAC пельӧс. B да C чутъяс пыр нуӧдӧма M чутын вомӧнассьытӧдз касательнӧйяс. Определитны ∠BMC.

54. Определитны описаннӧй пельӧслысь величинасӧ, йывсяньыс кӧ кытшвизьӧдз медматыс расстоянньӧыс радиус ыджда.

55. ‿AB = 40°24′. OA радиуссӧ нюжӧдӧм вылӧ пуктӧма AB хорда ыджда AC юкӧн да C чутсӧ ӧтлаалӧма B‐кӧд. Определитны ∠ACB.

56. ABC куимпельӧсаын C пельӧсыс веськыд. C шӧр чутсянь AC радиусӧн нуӧдӧма ADE дуга, коді гипотенузасӧ вомӧналӧ D чутын, а CB катетсӧ — E чутын. ∠B = 37°24′. Определитны AD да DE дугаяссӧ.

Сетӧм пельӧсӧс тӧрӧдысь сегмент.

57. ABC да ADC куимпельӧсаяслӧн AC ӧтувъя бок; AD да BC бокъясыс вомӧнасьӧны M чутын. B да D пельӧсъяс 40° ыдждаӧсь. B да D йывъяс костса расстоянньӧыс AB бокыс ыджда; ∠AMC = 70°. Определитны ABC да ADC куимпельӧсаяслысь пельӧсъяссӧ.

58. MN веськыд визь вылысь корсьны сэтшӧм чут, кысянь мед вӧлі сетӧм AB вундӧг тыдалӧ сетӧм пельӧс улын.

59. Вӧчны куимпельӧса, кор сетӧма подувтассӧ, йывдінса пельӧссӧ да судтасӧ.

60. Вӧчны куимпельӧса, кор сетӧма подувтассӧ, йывдінса пельӧссӧ да подувтас вылӧ нуӧдӧм медианасӧ.

61. Сетӧма ыджданас да положенньӧнас кык вундӧгӧс — a да b. Корсьны сэтшӧм чут, кысянь медым вӧлі тыдалӧ a вундӧг сетӧм A пельӧс улын, а b вундӧг — сетӧм B пельӧс улын.

62. Вӧчны параллелограммӧс диагональяс^вуджӧдӧмын ӧшыбка, гижӧма "диагональ". — А.В./^ да пельӧс серти.

Вписаннӧй да описаннӧй куимпельӧсаяс.

63. Веськыд пельӧса куимпельӧсалӧн гипотенузаыс 4 м ыджда. Определитны описаннӧй кытшвизьлысь радиуссӧ.

64. Кык ӧткузя бока куимпельӧсалӧн боквывса бокыс 2 см ыджда; йывдінса пельӧсыс 120°. Определитны описаннӧй кытшвизьлысь диаметрсӧ.

65. Медым O чут лоӧ ABC куимпельӧса гӧгӧр опишитӧм кытшвизьлӧн шӧр чутыс. Определитны ∠OAC, кор ∠B = 50°; 2) ∠B = 126°.

66. Веськыд пельӧса куимпельӧсаын ӧти ёсь пельӧсыс 25°; кутшӧм пельӧс улын тыдалӧ кыкнан катетыс описаннӧй кытшвизьса шӧр чутсяньыс?

67. Куимпельӧсаын кык пельӧс 100° да 50° ыдждаӧсь. Кутшӧм пельӧс улын тыдалӧны куимпельӧсалӧн бокъясыс вписаннӧй кытшвизьса шӧр чутсяньыс?

68. ABC куимпельӧсаыс кык ӧткузя бока; описаннӧй круглӧн OA радиусыс AC подувтасыскӧд вӧчӧ 20°38′ ыджда OAC пельӧс. Определитны ∠BAC. (Кык случай).

69. Вӧчны кык ӧткузя бока куимпельӧсаӧс подувтас да вписаннӧй круг радиус серти.

70. Кык ӧткузя бока куимпельӧсаын боквывса бокыс вписаннӧй кругса касанньӧ чутӧн юксьӧ 7 : 5 отношенньӧын (йывсянь пондӧмӧн). Корсьны боквывса бокыслысь подувтас дорӧ отношенньӧсӧ.

71. Веськыд пельӧса кык ӧткузя бока куимпельӧсаын вписаннӧй круглысь радиуссӧ пасъям r пыр, а периметр джынсӧ — p пыр. Определитны гипотенузасӧ.

72. Сетӧм круг гӧгӧр опишитны кык ӧткузя бока веськыд пельӧса куимпельӧсаӧс.

73. 4 см радиуса круг гӧгӧр опишитӧма веськыд пельӧса куимпельӧсаӧс; сылӧн гипотенузаыс 26 см. Корсьны куимпельӧсалысь периметрсӧ.

74. Сетӧм кругӧ впишитны куимпельӧсаӧс, кодлысь кык пельӧссӧ сетӧма.

75. Сетӧм круг гӧгӧр опишитны куимпельӧсаӧс, кодлысь кык пельӧссӧ сетӧма.

Вписаннӧй да описаннӧй нёльпельӧсаяс.

76. Веськыднёльпельӧсалӧн ичӧтджык бокыс 1 м ыджда; диагональяскостса ёсь пельӧсыс 60° ыджда. Корсьны описаннӧй круглысь радиуссӧ.

77. Веськыднёльпельӧсаын диагональыс бокыскӧд вӧчӧ 12°35′-а пельӧс. Тайӧ веськыднёльпельӧсаса йывъяснас кутшӧм нёль юкӧнӧ юксьӧ сы гӧгӧр опишитӧм кытшвизь?

78. 1) Сетӧм ромбӧ, 2) сетӧм дельтоидӧ впишитны круг.

79. Ромблӧн бокыс 8 см ыджда; ёсь пельӧсыс сылӧн 30° ыджда. Определитны вписаннӧй круглысь радиуссӧ.

80. Ромбӧ впишитӧма кытшвизь. Ромблӧн ёсь пельӧсыс 37° ыджда. Кутшӧм нёль юкӧнӧ кытшвизьыс юксьӧ ромб бокъясӧ касайтчан чутъясӧн?

81. Кык ӧткузя бока трапецияын подувтасбердса пельӧсыс 50° ыджда, а диагональяскостса пельӧсыс, коді паныдӧн видзӧдӧ боквывса бокыслы, 40° ыджда. Кӧні куйлӧ центрыс описаннӧй кытшвизьлӧн: трапеция пытшкын али ортсын?

82. Круг гӧгӧр опишитӧма трапеция, кодлӧн периметрыс 12 см ыджда. Определитны тайӧ трапециялысь шӧр визьсӧ.

83. Круг гӧгӧр опишитӧма кык ӧткузя бока 30° пельӧса трапеция, кодлӧн шӧр визьыс 1 м ыджда. Определитны круглысь радиуссӧ.

84. Вписаннӧй ABCD нёльпельӧсаын AC диагональыс BD диагональыслы перпендикулярнӧй да юкӧ сійӧс шӧри. ∠BAD = 70°23′42″. Определитны тайӧ нёльпельӧсалысь пельӧсъяссӧ.

85. Позьӧ-ӧ опишитны кытшвизьӧс нёльпельӧса гӧгӧр, кодлӧн пельӧсъясыс водзысь водзӧ (по порядку) относитчӧны кыдз: 1) 2 : 4 : 5 : 3; 2) 5 : 7 : 8 : 9?

86. Секторлӧн центральнӧй пельӧсыс 60°, а радиусыс R ыджда. Определитны тайӧ секторӧ впишитӧм круглысь радиуссӧ.

87. ABCD нёльпельӧсаысь сетӧма: ∠ABC = 116°; ∠ADC = 64°; ∠CAB = 35° да ∠CAD = 52°. Определитны диагональяскостса AB боклы воча пельӧссӧ.

88. 1) Описаннӧй нёльпельӧсалӧн куим бокыс (водзысь водзӧ пӧрадокӧн) относитчӧны кыдз 1 : 2 : 3. Определитны бокъяссӧ, тӧдам кӧ, мый периметрыс сылӧн 24 м ыджда.

2) Вписаннӧй нёльпельӧсалӧн куим пельӧсыс водзысь водзӧ относитчӧны кыдз 1 : 2 : 3. Определитны нёльпельӧсалысь пельӧсъяссӧ.

8 §. Пропорциональнӧй вундӧгъяс. Куимпельӧсаын биссектрисалӧн свойство.

Пропорциональнӧй вундӧгъяс.

1. Последовательнӧя пукталӧмӧн корсьны AB вундӧглысь CD вундӧг дорӧ отношенньӧ (25 чертёж).

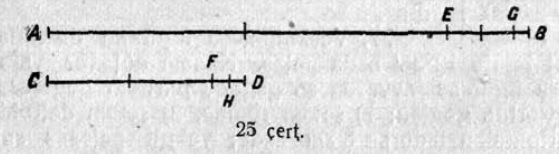
2. Корсьны (0,1-ӧдз точносьтӧн) ӧткузя бокъяса куимпельӧсаса судталысь бокыс вылӧ отношенньӧсӧ.

3. 1) AB вундӧг M чутӧн юксьӧ AM : MB = 1 : 2 отношенньӧын. Корсьны отношенньӧяс: AM : AB да MB : AB.

2) AB вундӧг K чутӧн юксьӧ m : n отношенньӧын. Корсьны отношенньӧяс: AK : AB да KB : AB.

4. 6 см кузя AB вундӧг вылын сетӧма C чут, кысянь A‐ӧдз 3,6 см; AB вундӧгӧс B сайӧ нюжӧдӧм вылысь корсьны сэтшӧм D чут, медым сылӧн A чутсянь расстоянньӧыс относитчис сысянь B чутӧдз расстоянньӧ дорӧ кыдз AC : CB.

5. Кык параллельнӧй улича вомӧнассьӧны ӧти чутысь петан кык уличаӧн. Параллельнӧй уличаяслӧн «лучевӧй уличаяс» костса юкӧнъясыс 0,75 км да 1,25 км ыдждаӧсь. Ӧти лучевӧй улича кузяыс первой параллельнӧй уличаӧдз трамвай мунӧ 15 мин. Кымын минут ковмас трамвайлы мунны сійӧ жӧ улича кузя мӧд параллельнӧй уличаӧдз (трамвайлӧн ӧд оз вежсьы)?

6. ∠A-лысь бокъяссӧ вомӧналӧны кык параллельнӧй веськыд визьяс: BC да DE (B да D шыпасъясӧн пасъям пельӧс ӧти боксьыс чутъяссӧ). Требуйтчӧ:

1) Определитны AE, кор AB = 8 м, AD = 12 м, AC = 10 м;

2) Определитны AB, кор AC = 12 м, AE = 16 м, AB + AD = 21 м;

3) Определитны AD, кор AC : AE = 3⁄11 : 0,6 да BD = 12 дм.

7. ABCD трапецияын AB да CD бокъяссӧ нюжӧдӧма мӧда-мӧдыскӧд M чутын вомӧнассьытӧдз. Колӧ:

1) определитны CM, кор AB = 1 м, CD = 15 дм, BM = 8 дм;

2) определитны BM, кор AB = 1,2 м, CD : CM = ⅙ : 0,25;

3) определитны CD, кор AB : BM = 17 : 9; CD − CM = 1,6 м.

8. BA да BD лоӧны ∠B-са ӧти бокыслӧн вундӧгъяс; BC да BE — мӧд бокыслӧн вундӧгъяс. Тӧдмавны, параллельнӧйӧсь-ӧ AC да DE веськыд визьяс, кор:

1) BA : AD = 3 : 4, BC = 1,2 м, BE = 2,8 м;

2) BD : AD = 11 : 8,5 да BC = 5⁄17CE;

3) BA = 7⁄13BD, BC = 2,8 м да CE = 2 м.

9. 1) Куимпельӧсалысь боквывса боксӧ юкӧма 5 юкӧнӧ да юкан чутъяссьыс нуӧдӧма подувтаслы параллельнӧй веськыдъясӧс. Подувтас 20 см ыджда. Определитны параллельнӧй веськыдъяслысь боквывса бокъяс костысь вундӧгъяссӧ.

2) Трапециялысь боквывса боксӧ юкӧма 8 юкӧнӧ да юкан чутъяссьыс нуӧдӧм подувтасыслы параллельнӧй веськыдъясӧс мӧд боквывса бокыскӧд вомӧнассьытӧдз. Трапециялӧн подувтасъясыс 50 см да 30 см ыдждаӧсь. Корсьны параллельнӧй веськыдъяслысь боквывса бокъяскостса кузьтаяссӧ.

10. Трапецияын подувтасъясыс 1,8 м да 1,2 м, боквывса бокъясыс 1,5 м да 0,9 м. Найӧс нюжӧдӧма мӧда-мӧдыскӧд вомӧнассьытӧдз. Определитны, кузя-ӧ нюжӧдӧма боквывса бокъяссӧ.

11. Пулысь судтасӧ мурталӧм вылӧ (26ʼ серп.) пусяньыс провешивайтӧны веськыд визь; сы вылын кутшӧмкӧ чутъясӧ бытшкӧны бедьяс сідз, медым налӧн A₁ да B₁ помъясыс да пулӧн M йылыс лоины ӧти веськыд визь вылын. Корсьны пулысь джудждасӧ, тӧдам кӧ, мый AD = m, AB = n, бедьяслӧн джудждаясыс a да b (m = 22,5 м; n = 1,25 м; a = 1,75 м да b = 2,55 м).

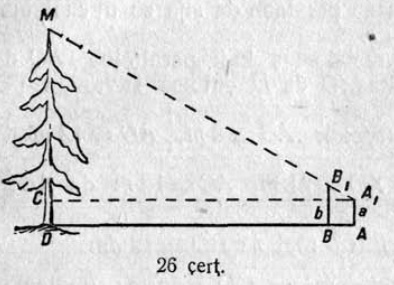
12. 27 чертёж вылын AB ∥ CD, FE ⊥ AB, OA = 4,8 см, OE = 4,5 см, OB = 5,4 см, OF = 1,5 см, AB = 4,8 см. Корсьны OD, OC, DC.

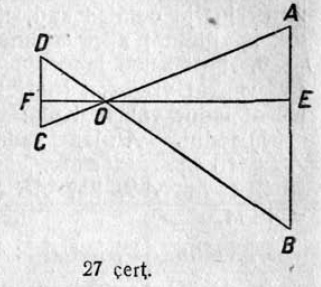
13. Шлагбаумлӧн дженьыд пельпомыс 0,75 м кузя, а кузьыс — 3,75 м (28 чертёж). Вылӧ-ӧ кайӧ кузь пельпомыслӧн помыс, кор дженьыдыслӧн помыс лэччӧ 0,5 м судтаӧдз? (Вӧчны чертёж).

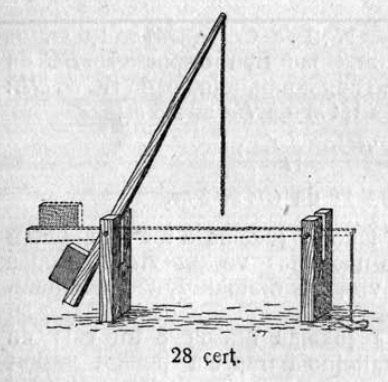
14. Куимпельӧсаын боквывса бокъясыслӧн подувтасыс вылӧ проекцияясыс 15 м да 27 м ыдждаӧсь; ыджыдджык боквывса бокыс 45 м. Кутшӧм юкӧнъясӧ сійӧ юксьӧ (йывсяньыс лыддьӧмӧн) подувтасыс шӧрӧ сувтӧдӧм перпендикулярӧн (судта положенньӧыслӧн кык случай)?

15. Пельӧс пытшкын либӧ пельӧс сайын сетӧм чут пыр нуӧдны веськыд визь сідз, медым сылӧн тайӧ чутӧн да пельӧс бокъясӧн артман юкӧнъясыс относитчисны кыдз m : n (видлыны случай, кор m = n).

16. 1) Корсьны геометрическӧй места чутъяслысь, кодъяслӧн сетӧм пельӧс бокъясӧдз расстоянньӧясыслӧн ӧти сійӧ жӧ m : n отношенньӧ.

2) Куимпельӧсаын корсьны сэтшӧм чут, медым сысянь бокъясыс вылӧ лэдзӧм перпендикуляръясыс вӧліны сетӧм m : n : p отношенньӧын.

Куимпельӧсаын биссектрисалӧн свойство.

17. BD — ABC куимпельӧсаын B пельӧсса биссектриса. Колӧ определитны:

1) AD да DC вундӧгъяс, кор AB = 10 м, BC = 15 м да AC = 20 м;

2) BC боксӧ, кор AD : DC = 8 : 5 да AB = 16 м;

3) AC боксӧ, кор AB : BC = 2 : 7 да DC − AD = 1 м.

18. Куимпельӧсаын 9 см да 6 см ыджда бокъяс костса пельӧссӧ юкӧма шӧри. Коймӧд бокыслӧн ӧти вундӧгыс лои сетӧм бокъяс пиысь ӧтиыс ыджда. Определитны коймӧд боксӧ.

19. D — ABC куимпельӧсаын BC бок вылын чут. Тӧдмавны, юкӧ-ӧ AD веськыд визьыс A пельӧссӧ шӧри, кор:

1) AB = 12 см, AC = 15 см, BD = 8 см, DC = 10 см;

2) AB = 12 м, AC = 56 м да BD : DC = 14 : 3;

3) AB = 5⁄11AC, BD = 2 м да DC = 4,5 м;

4) AB = 6 м, AC = 28 м да BD = 3⁄17BC.

20. ABC куимпельӧсаӧ впишитӧма ADEF ромб сідз, мый сылӧн D, E да F йывъясыс куйлӧны AB, BC да AC бокъяс вылын. Определитны BE да EC вундӧгъяс, AB кӧ = 14 см, BC = 12 см да AC = 10 см.

21. Куимпельӧсалӧн бокъясыс 51 см, 85 см да 104 см ыдждаӧсь. Нуӧдӧма кытшвизь, коді касайтчӧ кыкнан ичӧтджык бокъяс бердас, а шӧр чутыс ыджыдджык бок вылас. Кутшӧм юкӧнъясӧ ыджыдджык бокыс юксьӧ шӧр чутнас?

22. Кык ӧткузя бока куимпельӧсаын судтаыс 20 см ыджда, а подувтасыс боквывса бокыс вылӧ относитчӧ кыдз 4 : 3. Определитны вписаннӧй круглысь радиуссӧ.

23. Кык ӧткузя бока куимпельӧсаын вписаннӧй круглӧн шӧр чутыс судтасӧ юкӧ 12 : 5 отношенньӧын, а боквывса бокыс 60 см ыджда. Определитны подувтассӧ.

24. Кык ӧткузя бока куимпельӧсаын вписаннӧй круглӧн радиусыс 2⁄7 судта ыджда; тайӧ куимпельӧсалӧн периметрыс 56 см ыджда. Определитны сылысь бокъяссӧ.

25. AB хорда = 15 м, AC хорда = 21 м, BC хорда = 24 м. D чут — BC дугалӧн шӧрыс. Кутшӧм BE да EC юкӧнъясӧ AED веськыд визьӧн юксьӧ BC хорда?

26. ABC куимпельӧсаын сетӧма бокъяссӧ: a, b да c. BD — ∠B биссектриса; O — BD биссектрисалӧн C пельӧсса биссектрисакӧд вомӧнассянін чут. Колӧ определитны отношенньӧ OD : OB.

27. ABC куимпельӧсаын AB бокыс = 15 см да AC = 10 см; AD — A пельӧслӧн биссектриса; DE ∥ AB. Определитны AE, EC да DE.

28. ABC кык ӧткузя бока куимпельӧсаын BA бокыс = BC = a; AC бокыс = b; AN да CM — A да C пельӧсъясса биссектрисаяс. Определитны MN-лысь кузьтасӧ.

9 §. Куимпельӧсаяслӧн да унапельӧсаяслӧн подобие.

Подобнӧй куимпельӧсаяс.

1. Куимпельӧсалӧн бокъясыс относитчӧны кыдз 4 : 5 : 6; талы подобнӧй куимпельӧсалӧн медічӧт бокыс 0,8 м. Определитны мукӧд бокъяссӧ мӧд куимпельӧсаыслысь.

2. Куимпельӧсалӧн бокъясыс относитчӧны кыдз 2 : 5 : 4; сылы подобнӧй куимпельӧсалӧн периметрыс 55 м ыджда. Определитны мӧд куимпельӧсалысь бокъяссӧ.

3. Фабричнӧй труба вуджӧрлӧн кузьтаыс 35,8 м; сійӧ жӧ кадӧ муӧ бытшкӧм 1,9 м кузя бедьлӧн вуджӧрыс 1,62 м кузьта. Корсьны трубалысь джудждасӧ.

4. ABC да A₁B₁C₁ куимпельӧсаясын сетӧма, мый ∠A = ∠A₁ да ∠B = ∠B₁. Тайӧ куимпельӧсаяс кузя решитны со кутшӧм задачаяс:

1) сетӧма: a = 10; b = 14; a₁ = 25; c₁ = 20. Определитны c да b₁.

2) сетӧма: a = 35; a₁ = 21; c − c₁ = 8. Определитны c.

5. ABC да DEF куимпельӧсаясын ∠A = ∠E да ∠B = ∠D. AB бок = 16 см; BC = 20 см; DE = 12 см; AC − EF = 6 см. Определитны AC, EF да DF.

6. Кык ӧткузя бока кык куимпельӧсаын йывъясдінса пельӧсъясыс ӧтыдждаӧсь. Ӧти куимпельӧсаыслӧн подувтасыс 17 см, а бокыс 10 см ыдждаӧсь; мӧдыслӧн подувтасыс 8 см ыджда. Определитны сылысь боквывса боксӧ.

7. ABC да A₁B₁C₁ куимпельӧсаясын сетӧма, мый ∠B = ∠B₁ да B пельӧслӧн бокъясыс B₁ пельӧс бокъясысь 2,5 пӧв ыджыдджыкӧсь. Определитны AC да A₁C₁, налӧн кӧ суммаыс 4,2 м ыджда.

8. ABC да DEF куимпельӧсаясын ∠B = ∠D, AB = 4⁄3DE да DF = 0,75BC. Определитны AC да EF, налӧн кӧ разносьтыс 5 см ыджда.

9. Тӧдмавны, подобнӧйӧсь-ӧ куимпельӧсаяс, налӧн кӧ бокъясыс татшӧмӧсь:

1) 1 м, 1,5 м да 2 м; 10 см, 15 см да 20 см;

2) 1 м, 2 м да 15 дм; 12 дм, 8 дм да 16 дм;

3) 1 м, 2 м да 1,25 м; 10 см, 9 см да 16 см.

10. 1) ABC куимпельӧсаын AB бокыс = 15 м да AC = 20 м; AB бок вылӧ пуктӧма юкӧн AD = 10 м; AC бок вылӧ — юкӧн AE = 12 м. Подобнӧйӧсь-ӧ ABC да ADE куимпельӧсаяс?

2) Воддза задачаын AB да AC бокъяслысь кузьтаяссӧ кольны важсӧ да босьтны AD = 12 м да AE = 9 м. Лоӧны-ӧ сэк ABC да ADE куимпельӧсаяс подобнӧйӧсь?

11. AB — ӧти кытшвизьлӧн диаметрыс; AC — хордаыс. Вӧчӧма AB 13⁄17 ыджда DE диаметр вылӧ мӧд кытшвизь; сэн нуӧдӧма AC 13⁄17 ыджда DF хорда. Определитны EF, тӧдам кӧ, мый BC = 3,4 м.

12. 1) Ӧти куимпельӧсалӧн бокъясыс 0,8 м, 1,6 м, 2 м; сылы подобнӧй куимпельӧсалӧн периметрыс 5,5 м ыджда. Определитны мӧд куимпельӧсалысь бокъяссӧ.

2) Ӧти куимпельӧсалӧн периметрыс сылы подобнӧй мӧд куимпельӧсаса периметрысь 11⁄13 ыджда. Кык сходственнӧй боклӧн разносьтыс 1 м ыджда. Определитны тайӧ бокъяссӧ.

13. Военнӧй посъясӧс кӧзла устойяс вылын вӧчигӧн (29 чертёж), пос сьӧкталысь личкӧмсӧ бурджыка грунт вылӧ распределитӧм могысь, кӧзла кокъяс A да B помъясӧ тувъялӧны AB пӧв да быд кок гозсӧ йитӧны DE йитӧдӧн. Корсьны DE йитӧдлысь кузьтасӧ, тӧдам кӧ, мый кӧзлалӧн судтаыс h = 3 м; AB пӧвлӧн кузьтаыс 1,5 м ыджда да йитӧдсӧ AB пӧвсянь пуктӧма 0,5 м ылнаӧ.

14. Сетӧма ABC куимпельӧса да сы пытшкын AC-лы параллельнӧй DE вундӧг (D лоӧ AB вылын, E лоӧ BC вылын). Определитны DE-лысь кузьтасӧ:

1) AC кӧ = 20 см, AB = 17 см да BD = 11,9 см;

2) AC кӧ = 18 дм, AB = 15 дм да AD = 1 м.

15. Сетӧма ABC куимпельӧса да сы пытшкын AC-лы параллельнӧй DE вундӧг (D лоӧ AB вылын, E лоӧ BC вылын). Колӧ:

1) определитны AD, AB кӧ = 16 см, AC = 2 дм да DE = 15 см;

2) определитны AD : BD отношенньӧ, тӧдам кӧ, мый AC : DE = 5⁄7 : 4⁄11.

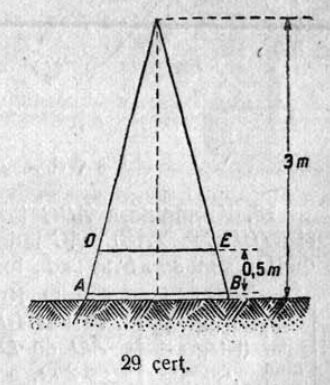
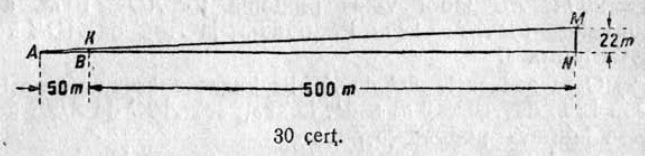
16. AB = 50 м полосаын — туйлӧн восьса участок (30 чертёж); MN = 22 м джуджда кӧлӧкӧльня вылын — неприятельлӧн наблюдательнӧй пункт. Джуджыдӧс-ӧ колӧ вӧчны кӧлӧкӧльнясянь 500 м сайын вертикальнӧй KB маска, медым сійӧн вевттьыны туйсӧ прӧтивник наблюдательысь?

17. ABC куимпельӧсалӧн бокъясыс a, b да c. Куимпельӧса пытшкын нуӧдӧма AC-лы MN параллельнӧй веськыдӧс сідз, мый AM = BN. Определитны MN.

18. ABC куимпельӧсаын нуӧдӧма BD веськыдӧс сідз, мый ∠BDC = ∠ABC, AC бок вылын сійӧ вӧчӧ вундӧгъяс: AD = 7 см да DC = 9 см. Определитны BC боксӧ да BD : BA отношенньӧ.

19. ABC куимпельӧсаын нуӧдӧма BD веськыдӧс сідз, мый ∠ABD = ∠BCA. Определитны AD да DC вундӧгъяс, AB кӧ = 2 м да AC = 4 м.

20. Вӧчны куимпельӧсаӧс, медым сійӧ вӧлі сетӧм куимпельӧсалы подобнӧй да периметрыс сылӧн мед вӧлі сетӧм кузьта ыджда.

21. Вӧчны куимпельӧсаӧс, кор сетӧма пельӧс, сы бердса бок да тайӧ боклысь коймӧд бок вылӧ отношенньӧсӧ.

22. Вӧчны куимпельӧсаӧс судта, йывбердса пельӧс да подувтасса вундӧгъяс отношенньӧ серти.

Трапецияын да параллелограммын пропорциональнӧй визьяс.

23. ABCD — сетӧм трапеция, та дырйи BC ∥ AD; O — диагональясыслӧн вомӧнассянін чутыс; AO = 8 см, OC = 1 дм да BD = 27 см. Определитны OB да OD.

24. Сетӧма ABCD трапеция, кӧн BC ∥ AD; O — диагональясыслӧн вомӧнассянін чутыс; BO : OD = 0,3 : ⅔; трапециялӧн шӧр визьыс = 29 см. Определитны подувтасъяссӧ да AO : OC отношенньӧ.

25. BD диагоналя ABCD трапецияын (кӧн BC ∥ AD) ∠ABD = ∠BCD. Сетӧма: BC = 10 см, DC = 15 см да BD = 20 см. Определитны AB да AD.

26. AC диагоналя ABCD трапецияын ∠ABC = ∠ACD. Определитны AC диагональсӧ, кор BC = 12 см да AD = 27 см.

27. Трапецияын подувтасъясыс относитчӧны кыдз 5 : 9, а ӧти боквывса бокыс 16 см ыджда. Кузя-ӧ сійӧс ковмас нюжӧдны, медым сійӧ вомӧнасяс мӧд боквывса бок нюжӧдӧмкӧд?

28. ABCD параллелограммын AB бокыс = 420 м. BC бок вылас босьтӧма E чут сідз, мый BE : EC = 5 : 7, да нуӧдӧма DE веськыдӧс, коді AB-лысь нюжӧдӧмсӧ вомӧналӧ F чутын. Определитны BF.

29. ABCD — сетӧм параллелограмм; F — AB бок нюжӧдӧм вылын чут; E — DF да AC-лӧн вомӧнассянін чут; AE : EC = m : n да AB = a. Определитны BF.

30. ABCD — сетӧм параллелограмм. Диагональясыс вомӧнассянін чут пырыс нуӧдӧма BC-лы перпендикулярнӧй визь, коді сійӧс вомӧналӧ E чутын, а AB-лысь нюжӧдӧмсӧ — F чутын. AB = a, BC = b, BF = c. Определитны BE.

Вписаннӧй да описаннӧй фигураяс.

31. Куимпельӧсаӧ впишитӧма параллелограмм, кодлӧн пельӧсыс куимпельӧсакӧд ӧтувъя. Куимпельӧсалӧн тайӧ пельӧссӧ йӧртысь бокъясыс 20 см да 25 см, а параллелограммлӧн налы параллельнӧй бокъясыс относитчӧны кыдз 6 : 5. Определитны параллелограммлысь бокъяссӧ.

32. ABC куимпельӧсаӧ впишитӧма ADEF ромбӧс сідз, мый налӧн A пельӧсыс ӧтувъя да E йылыс BC бок вылын; определитны ромблысь боксӧ, кор AB = c, AC = b.

33. Ромб йыв пыр ортсы нуӧдӧм веськыд визь вундӧ ромблысь кык боксӧ нюжӧдӧмысь p да q вундӧгъяс. Определитны ромблысь боксӧ.

34. Сетӧм сегментӧ впишитны квадрат сідз, медым сылӧн ӧти бокыс куйліс хорда вылын, а паныда боклӧн помъясыс — дуга вылын.

35. Сетӧм куимпельӧсаӧ впишитны квадрат сідз, медым сылӧн ӧти бокыс куйліс куимпельӧсаса ыджыдджык бокыс вылын, а воча пельӧсъяслӧн йывъясыс — куимпельӧсаса мӧд кык бокъяс вылас.

36. a подувтаса да h судтаа куимпельӧсаӧ впишитӧма квадрат сідз, мый сылӧн кык йылыс куйлӧны куимпельӧсаса подувтасыс вылын, а мӧд кыкыс — боквывса бокъяс вылас. Определитны квадратлысь боксӧ.

37. Сетӧм куимпельӧсаӧ впишитны веськыднёльпельӧса, кодлӧн бокъясыс медым относитчисны кыдз m : n.

38. 48 см кузя подувтаса да 16 см кузя судтаа куимпельӧсаӧ впишитӧма веськыднёльпельӧса, кодлӧн бокъясыс относитчӧны кыдз 5 : 9 да ыджыдджык бокыс куйлӧ куимпельӧсаса подувтас вылын. Определитны веськыднёльпельӧсалысь бокъяссӧ.

39. 30 см кузя подувтаса да 10 см кузя судтаа куимпельӧсаӧ впишитӧма веськыд пельӧса кык ӧткузя бока куимпельӧсаӧс сідз, мый сылӧн гипотенузаыс сетӧм куимпельӧсаса подувтасыслы параллельнӧй, а веськыд пельӧсыслӧн йылыс куйлӧ тайӧ подувтас вылас. Определитны гипотенузасӧ.

40. Куимпельӧсаӧ впишитӧма круг джын, кодлӧн кытшвизь джынйыс касайтчӧ подувтасас, а диаметрыс (боквывса бокъясыс вылын помъясӧн) подувтасыслы параллельнӧй. Определитны радиуссӧ, куимпельӧсалӧн кӧ подувтасыс a ыджда, а судтаыс h.

Смешаннӧй задачаяс.

41. ABC куимпельӧсаын C пельӧсыс — веськыд; AC = 6 см, CB = 12 см. BC бок вылын босьтӧма D чутӧс сідз, мый ∠ADC = 90° − B. Кутшӧм юкӧнъясӧ D чутыс юкӧ CB боксӧ?

42. ABC куимпельӧсаын сетӧма кык боксӧ: BC = 16 м да AC = 12 м да соответствуйтысь судтаясыслысь суммасӧ: AD + BE = 14 м. Определитны AD да BE.

43. Параллелограммлӧн бокъясыс 2 м да 16 дм; ыджыд бокъяскостса расстоянньӧыс 8 дм. Определитны ичӧт бокъяскостса расстоянньӧсӧ.

44. Параллелограммлӧн периметрыс 48 см ыджда да судтаясыс относитчӧны кыдз 5 : 7. Определитны налы соответствуйтысь бокъяссӧ.

45. Определитны хордалысь кузьтасӧ, сетӧма кӧ, мый радиус = r да хорда помсянь мӧд помӧдыс нуӧдӧм касательнӧйӧдз расстоянньӧ = a.

46. Кык кытшвизь касайтчӧны ортсысянь. Касанньӧ чут пыр нуӧдӧм веськыд визь кытшвизьясас вӧчӧ хордаяс, кодъяс пиысь ӧтиыс мӧдсьыс 13⁄5 ыджда. Определитны радиусъяссӧ, шӧр чутъяскостса расстоянньӧыс кӧ 36 см ыджда.

47. ABC — сетӧм куимпельӧса; CD лоӧ C пельӧслӧн биссектриса; E чут куйлӧ BC вылын, а DE ∥ AC. Определитны DE, BC кӧ = a да AC = b.

48. ABC — сетӧм куимпельӧса; BD — судта; AE лоӧ A пельӧслӧн биссектриса; EF лоӧ AC вылӧ перпендикуляр. Определитны EF, BD кӧ = 30 см да AB : AC = 7 : 8.

49. Параллелограммӧ впишитӧма ромбӧс сідз, мый сылӧн бокъясыс параллельнӧйӧсь параллелограммса диагональясыслы, кодъяс l да m ыдждаӧсь. Определитны ромблысь боксӧ.

50. Нёль параллельӧс, кодъяс костса последовательнӧй расстоянньӧясыс относитчӧны кыдз 2 : 3 : 4, вундӧма ӧти чутӧ воан кык веськыд визьӧн. Нёль артмӧм параллельнӧй вундӧгъяс пиысь дорсаясыс 60 дм да 96 дм ыдждаӧсь. Определитны шӧр вундӧгъяссӧ.

51. ABC куимпельӧсаын нуӧдӧма BA-сянь BC-ӧ DE веськыдӧс, AC-лы параллельнӧя. Сетӧма: AB = 24 м, BC = 32 м, AC = 28 м да AD + CE = 16 м. Определитны DE.

52. AD да BE — ABC куимпельӧсалӧн O чутын вомӧнасян судтаясыс. Сетӧма: AD + BE = 35 дм; AO = 9 дм да BO = 12 дм. Определитны OE да OD.

53. 100 дм кузя боквывса бока да 60 дм подувтаса, кык ӧткузя бока куимпельӧсаӧ впишитӧма круг. Определитны боквывса бокъяс вывса касанньӧ чутъяскостса расстоянньӧсӧ.

54. Секторлӧн радиус r ыджда, дугаыслӧн хордаыс a ыджда. Определитны тайӧ секторӧ впишитӧм круглысь радиуссӧ.

Подобнӧй унапельӧсаяс.

55. Ӧти витпельӧсалӧн бокъясыс: 35 см, 14 см, 28 см, 21 см да 42 см ыдждаӧсь; талы подобнӧй витпельӧсалӧн медічӧт бокыс 12 см ыджда. Определитны сылысь мукӧд бокъяссӧ.

56. Ӧти нёльпельӧсалӧн бокъясыс относитчӧны кыдз 1 : ½ : ⅔ : 2; сылы подобнӧй нёльпельӧсалӧн периметрыс 75 м ыджда. Определитны мӧд нёльпельӧсалысь бокъяссӧ.

57. Ӧти нёльпельӧсалӧн бокъясыс 10 дм, 15 дм, 20 дм да 25 дм; сылы подобнӧй нёльпельӧсаын медыджыд да медічӧт бокъясыслӧн суммаыс 28 дм ыджда. Определитны мӧд нёльпельӧсалысь бокъяссӧ.

58. Кык подобнӧй унапельӧсалӧн медыджыд бокъясныс 35 м да 14 м ыдждаӧсь, а периметръясыслӧн разносьтыс 60 м. Определитны периметръяссӧ.

59. Джодж вылӧ цементнӧй плитаяс вӧчысь завод лӧсьӧдіс веськыднёльпельӧса плитаяс вылӧ нормальнӧй форма (стандарт) — сэтшӧмӧс, мый медым плита джынйыс BCFE вӧлі быдса ABCD плитаыслы подобнӧй. Корсьны татшӧм плитаяс бокъяслысь отношенньӧсӧ (31 чертёж).

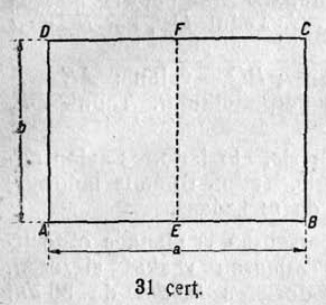
60. ABCD параллелограммын бокъясыс: AB = a да BC = b. EF веськыд вундӧ ABEF параллелограмм, коді лоӧ ABCD-лы подобнӧй. Определитны BE.

10 §. Куимпельӧсаясын да некымын сикас нёльпельӧсаясын линейнӧй элементъяс костас лыда зависимосьт.

Веськыд пельӧса куимпельӧсаын пасйӧны: a да b — катетъяс; c — гипотенуза; a_c да b_c пасъясӧн пасйӧма a да b катетъяслысь гипотенуза вылӧ проекцияяс; h — веськыд пельӧс йывсянь судта. Оз ков вунӧдны, мый визьяссӧ мурталӧма ӧти сійӧ жӧ единичаын.

Веськыд пельӧса куимпельӧсаын пропорциональнӧй вундӧгъяс.

1. Артавны гипотенуза, сетӧма кӧ кыкнан катетсӧ:

1) 12 см да 35 см; 2) 56 см да 33 см; 3) 4 м да 9 дм; 4) 60 см да 91 см; 5) 21 да 3¼; 6) 3⁄2 да 7⁄16; 7) 16,8 да 2,6; 8) 5 да 6.

2. Артавны мӧд катетсӧ, сетӧма кӧ гипотенузасӧ да первой катетсӧ:

1) 289 да 240^ 2 задачаын да мукӧд уна случайясын артасигӧн бурджык овлӧ квадратъяслысь разносьтсӧ вежны суммалысь разносьт вылӧ произведенньӧӧн./^; 2) 269 да 69; 3) 145 да 143; 4) 42,5 да 6,5; 5) 17 да 15​2⁄5; 6) 10 да 7.

3. Кык сетӧм элемент кузя определитны веськыд пельӧса куимпельӧсалысь мукӧд нёль элементсӧ:

1) a = 15, b = 20; 2) a = 24, b = 7; 3) a = 4, b = 5; 4) a = 100, c = 125; 5) b = 65, c = 169; 6) a = 600, c = 625; 7) a = 6, a_c = 3,6; 8) b = 7, b_c = 1,96; 9) c = 29, a_c = 15​6⁄29; 10) c = 3, b_c = 2; 11) a_c = 1½, b_c = 2⅔; 12) a_c = 2, b_c = 18; 13) a = 136, h = 120; 14) b = 9, h = 8​32⁄41.

4. Сетӧма кык вундӧглысь суммасӧ да средньӧй пропорциональнӧйсӧ. Вӧчны вундӧгъяссӧ.

5. Сетӧма кык вундӧглысь разносьтсӧ да средньӧй пропорциональнӧйсӧ. Вӧчны вундӧгъяссӧ.

6. Докажитны, мый веськыд пельӧса куимпельӧсаын ab = ch.

7. Катетъяс относитчӧны кыдз 5 : 6, гипотенуза 122 см. Корсьны гипотенузалысь вундӧгъяссӧ (судтаӧн артманъяссӧ).

8. Катетъяс относитчӧны кыдз 3 : 2, судтаыс юкӧ гипотенузасӧ вундӧгъясӧ, кодъяс пиысь ӧтиыс мӧдсьыс 2 м-ӧн ыджыдджык. Определитны гипотенузасӧ.

9. Катетъяс относитчӧны кыдз 3 : 7, гипотенуза вылӧ нуӧдӧм судта 42 см ыджда. Определитны гипотенузалысь вундӧгъяссӧ.

10. Докажитны, мый кык ӧткузя бока трапецияӧ впишитӧм кытшвизьлӧн диаметрыс эм трапецияса параллельнӧй бокъясыс костын средньӧй пропорциональнӧй.

11. Докажитны, мый катетъяс квадратъяслӧн отношенньӧыс гипотенуза вылӧ найӧ проекцияяслӧн отношенньӧ ыджда.

12. 1) Вӧчны кык вундӧгӧс, кодъяслӧн квадратъясыс относитчӧны кыдз m : n.

2) Вӧчны сэтшӧм кык вундӧг, медым найӧ относитчисны кыдз кык сетӧм вундӧгъяслӧн квадратъясыс.

Пифагорлӧн теорема.

13. Тӧдмавны, кутшӧм последовательнӧй куим быдса лыдъясӧн вермӧны петкӧдчыны веськыд пельӧса куимпельӧсалӧн бокъясыс.

14. Кык фабричнӧй зданньӧ костын материалъяс передача вылӧ вӧчӧма пӧлыня жӧлӧб. Зданньӧяс костыс 10 м; жӧлӧблӧн помъясыс мусянь 8 м да 4 м вылнаынӧсь. Определитны жӧлӧблысь кузьтасӧ.

15. 1) Веськыд пельӧспытшса чутӧс ылӧстӧма пельӧс бокъяссяньыс a да b сайӧ. Корсьны чутсянь веськыд пельӧс йылӧдз расстоянньӧсӧ.

2) Веськыднёльпельӧсалӧн бокъясыс 60 см да 91 см. Ыджыд-ӧ сылӧн диагональыс?

16. Колӧ фрезуйтны 32 мм бока квадратнӧй головка. Ыджыд-ӧ колӧ та вылӧ гӧгрӧс кӧртлӧн медічӧт диаметрыс?

17. 1) Квадратлӧн бокыс a ыджда. Ыджыд-ӧ сылӧн диагональыс?

2) Определитны квадратлысь боксӧ, сійӧ кӧ диагональсьыс 2 см-ӧн ичӧтджык.

18. Керлӧн диаметрыс 12 см. Позьӧ-ӧ тайӧ керсьыс лӧсавны 10 см бока квадратнӧй брус?

19. 1) Веськыднёльпельӧсалӧн бокъясыс a да b. Определитны описаннӧй круглысь радиуссӧ.

2) Кругӧ впишитӧма веськыднёльпельӧсаӧс, кодлӧн бокъясыс относитчӧны кыдз 8 : 15. Определитны тайӧ бокъяссӧ, круглӧн кӧ радиусыс 34 см ыджда.

20. 1) Веськыд пельӧса куимпельӧсалӧн катетъясыс 8 дм да 18 см. Определитны описаннӧй круглысь радиуссӧ.

2) Веськыд пельӧса куимпельӧсалӧн катетъясыс 16 см да 12 см. Определитны гипотенузаыслысь медианасӧ.

21. 1) Кык ӧткузя бока куимпельӧсаын боквывса бокыс 17 см, подувтасыс 16 см. Определитны судтасӧ.

2) Определитны кык ӧткузя бока куимпельӧсалысь бокъяссӧ, судтаыс кӧ сылӧн 35 см ыджда, а подувтасыс относитчӧ боквывса бокыс дорӧ кыдз 48 : 25.

3) Кык ӧткузя бока куимпельӧсаын подувтасыс 4 см, а сы бердса пельӧсыс 45°. Определитны боксӧ.

22. Стропильнӧй фермалӧн AB да CB кокъясыс 9 м кузяӧсь да AC пролётыс 15 м (32 чертёж). Определитны фермалысь BD судтасӧ.

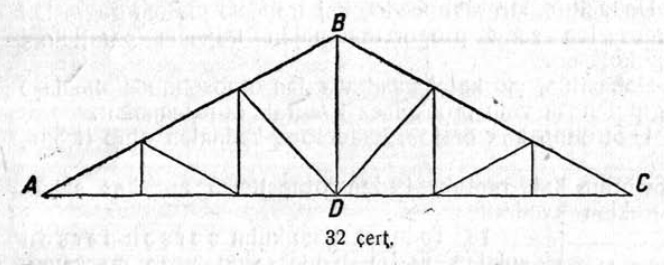
23. 1) Веськыд пельӧслӧн биссектрисаыс веськыд пельӧса куимпельӧсалысь гипотенузасӧ юкӧ 2​1⁄7 м да 2​6⁄7 м ыджда вундӧгъясӧ. Определитны катетъяссӧ.

2) Веськыд пельӧса куимпельӧсаын катетъясыс 16 см да 20 см^Оз лӧсяв вочакывкӧд. — А.В./^. Веськыд пельӧс йывсяньыс нуӧдӧма судта да биссектриса. Кутшӧм вундӧгъясӧ юксис гипотенуза?

24. 1) Ӧткузя бокъяса куимпельӧсалысь определитны судтасӧ a бок сертиыс.

2) Ӧткузя бокъяса куимпельӧсалысь определитны боксӧ h судта сертиыс.

3) Ӧткузя бокъяса куимпельӧсаын судтаыс боксьыс m-ӧн ичӧтджык. Определитны боксӧ.

4) Веськыд пельӧса куимпельӧсаын ӧти пельӧс 30° да ыджыдджык катетыс 6 см ыджда. Определитны тайӧ куимпельӧсалысь мукӧд кык боксӧ.

25. 1) Куимпельӧсалӧн боквывса бокъясыс: a = 25 см да b = 30 см, судтаыс h_c = 24 см. Определитны c подувтассӧ.

2) Куимпельӧсаын подувтасбердса ыджыдджык пельӧсыс 45° ыджда, судтаыс подувтассӧ юкӧ 20 см да 21 см ыджда юкӧнъясӧ. Определитны боквывса ыджыдджык боксӧ.

3) Ӧти чутсянь сетӧм веськыд визь вылӧ нуӧдӧма перпендикулярӧс да кык пӧлыняӧс. Определитны перпендикулярлысь кузьтасӧ, пӧлыняяс кӧ 41 см да 50 см ыдждаӧсь да налӧн проекцияясыс сетӧм веськыд вылӧ относитчӧны кыдз 3 : 10.

26. 1) Ромблӧн диагональясыс 24 см да 70 см. Определитны боксӧ.

2) Определитны ромблысь диагональяссӧ, найӧ кӧ относитчӧны кыдз 3 : 4 да периметрыс 1 м ыджда.

27. 1) Кык ӧткузя бока трапецияын подувтасъясыс 10 см да 24 см, а боквывса бокыс 25 см. Определитны трапециялысь судтасӧ.

2) Кык ӧткузя бока трапецияын боквывса бокыс 41 см, судтаыс 4 дм да шӧр визьыс 45 см ыдждаӧсь. Определитны подувтасъяссӧ.

28. Веськыд туйлы, сысянь 500 м сайын, параллельнӧя расположитчӧма стрелокъяслӧн чеп; ӧт-мӧдар медся дорса стрелокъяскостса расстоянньӧыс 120 м; пуля мунӧ 2,8 км сайӧ. Ыджыд-ӧ туйлӧн участок тайӧ чеп лыйлӧм улын?

29. 33 чертёж вылын мыччӧдӧма потайнӧй головкаа ОСТ 302 заклёпка (ОСТ — общесоюзнӧй стандарт). α пельӧс = 60°. Артавны:

1) D, кор d = 16,5 мм да h = 7,5 мм;

2) d, кор D = 30 мм да h = 9,5 мм;

3) h, кор D = 35 мм да d = 22 мм.

Гижны формула, коді йитӧ мӧда-мӧдыскӧд D, d, h.

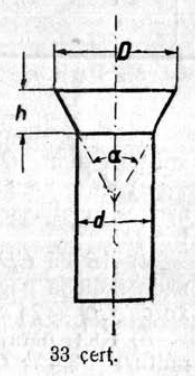
30. 1) ABC куимпельӧсаын нуӧдӧма AD судта. Докажитны, мый AB² − AC² = BD² − CD².

2) M кӧ — ABC куимпельӧсаын AD судтаыс вылын кутшӧмкӧ чут, AB² − AC² = BM² − CM². Докажитны.

31. 1) Докажитны, мый веськыд пельӧса трапецияын диагональяссьыс квадратъясыслӧн разносьтыс подувтасъяссьыс квадратъяс разносьт ыджда.

2) Веськыд пельӧса трапецияын ичӧтджык диагональыс боквывса пӧлыня бокыс ыджда. Определитны ыджыдджык диагональсӧ, боквывса пӧлыня бокыс кӧ a ыджда да ичӧтджык подувтасыс — b ыджда.

32. Кӧрт листысь колӧ штампуйтны 28 мм диаметра гӧгрӧс шайбаяс. Корсьны расстоянньӧсӧ веськыд визьяс костысь, кодъяс вылӧ колӧ пуктавны шайбаяслысь шӧр чутъяссӧ (34 чер.).

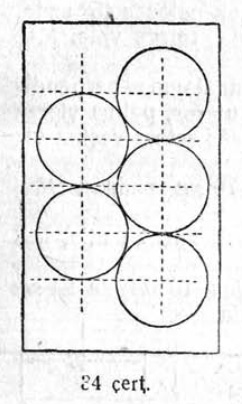
33. 1) Круглӧн радиусыс 89 дм, хорда 16 м. Определитны хордасянь шӧр чутӧдз расстоянньӧсӧ.

2) O — шӧр чут, ACB — хорда; OCD — хордалы перпендикулярнӧй радиус. OC = 9 см, CD = 32 см. Определитны хордасӧ.

3) Кык вомӧнассян кытшвизьяслӧн радиусъясыс 13 см да 15 см ыдждаӧсь да ӧтувъя хордаыс 24 см ыджда. Определитны шӧр чутъяскостса расстоянньӧсӧ.

4) AB да CD лоӧны R = 15 см радиуса кытшвизьын O шӧр чутсянь ӧтар-мӧдар сайын куйлысь параллельнӧй^Вуджӧдӧмын "параллельнӧй" кыв вунӧдӧма. — А.В./^ хордаяс; AB хорда = 18 см, CD хорда = 24 см. Определитны хордаяскостса расстоянньӧсӧ.

5) AB да CD лоӧ R = 30 см радиуса кытшвизьын O шӧр чутсянь ӧтар сайын куйлысь параллельнӧй^Вуджӧдӧмын "параллельнӧй" кыв вунӧдӧма. — А.В./^ хордаяс; AB хорда = 48 см, CD хорда = 36 см. Определитны хордаяскостса расстоянньӧсӧ.

34. Шкивлысь диаметрсӧ мурталӧм вылӧ пуктісны штангенциркуль сідз, кыдз индӧма 35 чертёж вылын. Штангенциркуль кокъяслӧн кузьтаыс s = 25 мм, найӧ помъяскостса расстоянньӧыс l = 200 мм;

1) определитны D диаметрлысь кузьтасӧ;

2) петкӧдны формула, коді медым мыччӧдіс D-лысь s да l-ысь зависимосьт.

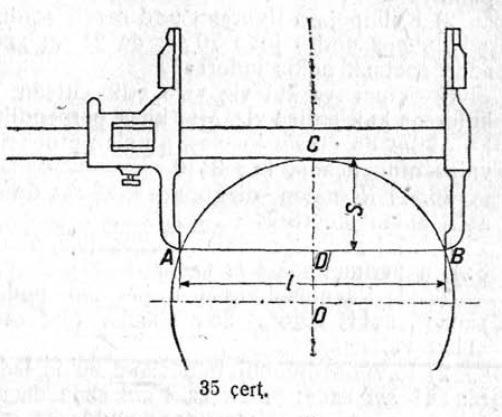
35. Сегментын хордаыс a ыджда, судтаыс — h. Определитны круглысь радиуссӧ.

36. Круглӧн радиусыс 25 см, кык параллельнӧй хорда 14 см да 40 см ыдждаӧсь. Определитны на костысь расстоянньӧсӧ.

37. Диаметр ӧти помсяньыс сылы параллельнӧй хорда помъясӧдз 13 см да 84 см. Определитны круглысь радиуссӧ.

38. 1) 36 см радиуса кытшвизь бердӧ нуӧдӧма шӧр чутсянь 85 см сайса чутысь касательнӧйӧс. Определитны сылысь кузьтасӧ.

2) Ӧтувъя чутысь кытшвизь бердӧ нуӧдӧма кык касательнӧйӧс. Кытшвизьлӧн радиусыс 11 см да касательнӧйяслӧн суммаыс 120 см ыдждаӧсь. Определитны шӧр чутсянь касательнӧйяс заводитчан чутӧдзыс расстоянньӧсӧ.

3) 7 см радиуса кытшвизь бердӧ нуӧдӧма шӧр чутсянь 25 см сайса ӧти чутысь кык касательнӧйӧс. Определитны касанньӧ чутъяскостса расстоянньӧсӧ.

39. R да r радиусъяса кык круг касайтчӧны ортсысянь. Ӧти кругса шӧр чутсьыс нуӧдӧма мӧд круг бердас касательнӧйӧс, артмӧм касанньӧ чутсьыс нуӧдӧма первой круг бердас касательнӧйӧс. Определитны бӧръя касательнӧйыслысь кузьтасӧ.

40. 1) Кык круг касайтчӧны ортсысянь. Определитны налысь ӧтувъя ортсыса касательнӧйыслысь кузьтасӧ (касанньӧ чутъяс костсьыс), радиусъясыс кӧ 16 см да 25 см ыдждаӧсь.

2) Кык круглӧн радиусъясыс 27 см да 13 см ыдждаӧсь, а шӧр чутъяскостса расстоянньӧыс 50 см ыджда. Определитны ӧтувъя касательнӧйясыслысь кузьтаяссӧ.

41. Ӧти чутысь ӧти кытшвизь бердӧ нуӧдӧм касательнӧй да вундысь мӧда-мӧдыслы перпендикулярнӧйӧсь. Касательнӧйыс 12 м ыджда, вундысьлӧн пытшкӧс юкӧныс 10 м ыджда. Определитны кытшвизьлысь радиуссӧ.

42. AB да CD — параллельнӧй веськыдъяс; AC — вундысь; E да F лоӧны C да A пельӧсъясса биссектрисаяскӧд AB да CD веськыдъяслӧн вомӧнассянін чутъяс. Сетӧма: AF = 96 см да CE = 110 см. Определитны AC.

43. Тшӧтшыд пельӧса кык ӧткузя бока ABC куимпельӧсаын AC подувтасыс 32 м да боквывса бокыс 20 м. B йывсьыс боквывса бокыслы нуӧдӧма подувтасыскӧд вомӧнассьытӧдз перпендикуляр. Кутшӧм юкӧнъясӧ сійӧ вундӧ подувтассӧ?

44. AC катет = 15 см; CB катет = 8 см. C чутысь кыдз шӧр чутысь нуӧдӧма CB радиусӧн дуга, коді гипотенузасьыс вундӧ BD юкӧн. Определитны BD.

45. Веськыд пельӧса куимпельӧсаын веськыд пельӧс йывсянь ичӧтджык катет ыджда радиусӧн нуӧдӧм дуга гипотенузасӧ юкӧ 98 см да 527 см кузя вундӧгъясӧ (ичӧт катетсяньыс заводитӧмӧн). Определитны катетъяссӧ.

46. AB — круглӧн диаметр; BC — касательнӧй; D — кытшвизькӧд AC веськыдлӧн вомӧнассянін чут. Сетӧма: AD = 32 см да DC = 18 см. Определитны радиуссӧ.

47. AB — диаметр; BC да CDA — касательнӧй да вундысь. Определитны отношенньӧ CD : DA, BC кӧ радиус ыджда.

Веськыд пельӧса куимпельӧсаын биссектриса.

48. Веськыд пельӧса куимпельӧсаын веськыд пельӧслӧн биссектрисаыс гипотенузасӧ юкӧ 7 : 9 отношенньӧын. Кутшӧм отношенньӧын юкӧ сійӧс судтаыс (юкӧнъяссӧ сійӧ жӧ пӧрадокӧн лыддьӧмӧн)?

49. Определитны катетъяс, веськыд пельӧсса биссектрисаыс кӧ гипотенузасӧ юкӧ 15 см да 20 см ыджда юкӧнъясӧ.

50. Кык ӧткузя бока веськыд пельӧса куимпельӧсаын катетыс a ыджда. Кутшӧм юкӧнъясӧ юкӧ сійӧс воча куйлысь пельӧслӧн биссектрисаыс?

51. Веськыд пельӧса куимпельӧсаын ёсь пельӧсыслӧн биссектрисаыс юкӧ катетсӧ m да n вундӧгъясӧ (m > n). Определитны мӧд катетсӧ да гипотенузасӧ.

52. Веськыд пельӧса куимпельӧсаын, кодлӧн катетъясыс 15 дм да 2 м ыдждаӧсь, нуӧдӧма: веськыд пельӧс йывсяньыс судтаӧс да биссектрисаясӧс кыкнан пельӧссьыс, кодъясӧс артмӧдӧны судтаыс да катетъясыс. Определитны гипотенузалысь биссектрисаяскостса вундӧгсӧ.

53. Веськыд пельӧса ABC куимпельӧсаын катет BC = 6 см да гипотенуза AB = 10 см. ABC пельӧсын да сыкӧд орччаын нуӧдӧма биссектрисаясӧс AC катетӧс да сылысь нюжӧдӧмсӧ D да E чутъясын вомӧнавтӧдз. Определитны DE-лысь кузьтасӧ.

54. Кык ӧткузя бока ABC куимпельӧсаын сетӧма: AB боквывса бок = 10 м да AC подувтас = 12 м. A да C пельӧсъяслӧн биссектрисаясыс вомӧнассьӧны D чутын. Определитны BD.

55. 1) Кык ӧткузя бока куимпельӧсалӧн подувтасыс 30 см да боквывса бокыс 39 см. Определитны вписаннӧй круглысь радиуссӧ.

2) Кык ӧткузя бока куимпельӧсаын вписаннӧй круглӧн шӧр чутыс судтасӧ юкӧ 17 : 15 отношенньӧын. Подувтасыс 60 см ыджда. Корсьны тайӧ круглысь радиуссӧ.

Веськыд пельӧса куимпельӧсаын, ромбын да трапецияын судта да бокъяс.

56. B чутысь нуӧдӧма сетӧм веськыд визь вылӧ BC перпендикуляр да BA пӧлыняӧс. AC вылын босьтӧма D чут да BD веськыдӧс нюжӧдӧма AC-лы перпендикулярнӧй AE веськыдкӧд E чутын вомӧнассьытӧдз. Определитны AE, BA кӧ = 53 дм, AD = 8 дм да DC = 20 дм.

57. 1) Кык ӧткузя бока куимпельӧсаын подувтасыс 30 дм, судтаыс = 20 дм. Определитны боквывса судтасӧ.

2) Кык ӧткузя бока куимпельӧсаын ӧтыджда бокъяс костӧд нуӧдӧм судтаыс = 3 дм, а бокса судтаыс = 4 дм. Определитны тайӧ куимпельӧсалысь бокъяссӧ.

3) Ромблӧн диагональясыс 14 дм да 48 дм ыдждаӧсь. Определитны сылысь судтасӧ.

58. 1) AB гипотенуза = 34 см.; BC катет 16 см. Определитны гипотенузалы шӧрас сувтӧдӧм перпендикулярлысь AC катеткӧд вомӧнасьтӧдз кузьтасӧ.

2) Круглӧн радиусыс = r. Определитны хордалысь кузьтасӧ, кодӧс нуӧдӧма сетӧм диаметр помысь сылы перпендикулярнӧй радиус шӧр пыр.

59. ABC веськыд пельӧса куимпельӧсаын катет AC = 16 дм да катет BC = 12 дм. B шӧр чутысь BC радиусӧн нуӧдӧма кытшвизь да сы бердӧ гипотенузалы параллельнӧй касательнӧйӧс (та дырйи куимпельӧсаыс да касательнӧйыс гипотенузасяньыс куйлӧны разнӧй бокъясын). BC катетсӧ нюжӧдӧма нуӧдӧм касательнӧйкӧд вомӧнассьытӧдз. Определитны, уна-ӧ нюжӧдӧма катетсӧ.

60. Ӧти чутысь круг бердӧ нуӧдӧма кык касательнӧйӧс. Касательнӧйлӧн кузьтаыс 156 дм ыджда, касанньӧ чутъяскостса расстоянньӧыс 120 дм ыджда. Определитны круглысь радиуссӧ.

61. Веськыд пельӧса трапецияын подувтасъясыс 17 дм да 25 дм, боквывса ыджыдджык бокыс 10 дм. Тайӧ бок шӧрсьыс нуӧдӧма сылы перпендикуляр боквывса мӧд боксӧ нюжӧдӧмыскӧд вомӧнассьытӧдз. Определитны тайӧ перпендикулярыслысь кузьтасӧ.

Веськыд пельӧса куимпельӧса вылӧ смешаннӧй задачаяс.

62. AC да CB — катетъяс; CD — судта; DE ∥ BC; определитны отношенньӧ AE : EC, кор AC : CB = 4 : 5.

63. AC да CB — катетъяс; CD — судта; DE ⊥ AC да DF ⊥ CB. Определитны DE да DF, AC кӧ = 75 дм да BC = 100 дм.

64. Кык ӧткузя бока кык куимпельӧсаын боквывса бокъясыс ӧткузяӧсь, а йывъясбердса пельӧсъясыслӧн суммаыс 180° ыджда. Подувтасъясыс относитчӧны кыдз 9 : 40, а боквывса бокыслӧн кузьтаыс 41 дм. Определитны подувтасъяссӧ.

65. 1) Куимпельӧсаын подувтасыс = 60 м, судтаыс = 12 м да подувтасса медианаыс = 13 м. Определитны боквывса бокъяссӧ.

2) Веськыд пельӧса куимпельӧсаын корсьны катетъясыслысь отношенньӧсӧ, веськыд пельӧс йывсьыс петысь судтаыс да медианаыс кӧ относитчӧны кыдз 40 : 41.

66. Определитны кык ӧткузя бока куимпельӧса гӧгӧр нуӧдӧм круглысь радиуссӧ, кор куимпельӧсалӧн подувтасыс да боквывса бокыс соответственнӧй та ыдждаӧсь: 1) 6 дм да 5 дм; 2) 24 м да 13 м.

67. Веськыд пельӧса куимпельӧсаын катетъясыс 13 дм да 84 дм ыдждаӧсь. Определитны вписаннӧй круглысь радиуссӧ.

68. Ӧтиыс мӧд саяс куйлысь кык кытшвизьлӧн шӧр чутъяскостса расстоянньӧыс 65 дм ыджда; ӧтувъя ортсыса касательнӧйыслӧн касанньӧ чутъяскостса кузьтаыс 63 дм ыджда; ӧтувъя пытшкӧс касательнӧйыслӧн кузьтаыс 25 дм ыджда. Определитны кытшвизьяслысь радиусъяссӧ.

69. Кык параллельнӧй хордалӧн кузьтаясыс 40 дм да 48 дм; на костса расстоянньӧыс 22 дм. Определитны круглысь радиуссӧ.

70. Круг гӧгӧр опишитӧм кык ӧткузя бока трапецияын подувтасъясыс 36 см да 1 м ыдждаӧсь. Определитны круглысь радиуссӧ.

71. 12 см ыджда радиуса круг гӧгӧр опишитӧма кык ӧткузя бока трапеция, кодлӧн боквывса боклӧн кузьтаыс 25 см. Определитны тайӧ трапециялысь подувтасъяссӧ.

72. r радиуса круг гӧгӧр опишитӧма кык ӧткузя бока трапеция, кодлӧн параллельнӧй бокъясыс относитчӧны кыдз m : n. Определитны тайӧ трапециялысь бокъяссӧ.

73. AB да AC — O шӧр чута ӧти круг бердӧ касательнӧйяс; M лоӧ AO веськыдлӧн кытшвизькӧд вомӧнассянін чут; DME — M пыр нуӧдӧм касательнӧйлӧн AB да AC костса вундӧг. Определитны DE-лысь кузьтасӧ, кругыслӧн кӧ радиусыс 15 дм ыджда да AO расстоянньӧыс = 39 дм.

74. Веськыд пельӧса куимпельӧсалӧн катетъясыс 15 дм да 20 дм. Определитны вписаннӧй кругса шӧр чутсянь гипотенуза вылӧ нуӧдӧм судтаӧдз расстоянньӧсӧ.

75. ABC веськыд пельӧса куимпельӧсаын веськыд пельӧс C йывсянь гипотенуза вылас лэдзӧма перпендикуляр да сы вылын кыдз диаметр вылын нуӧдӧма кытшвизьӧс, коді CA да CB катетъяс вылын сетӧ пытшкӧс вундӧгъяс: m да n. Определитны катетъяссӧ (m = 12; n = 18).

76. Веськыд пельӧса куимпельӧсаын катетъясыс 75 дм да 100 дм ыдждаӧсь. Гипотенуза вундӧгъяс вылын, кодъяс артмӧны судтаӧн, нуӧдӧма сетӧм куимпельӧсалань круг джынъясӧс. Определитны катетъяслысь вундӧгъяссӧ, кодъяс лоӧны тайӧ круг джынъяс пытшкын.

77. Кык круг кӧ касайтчӧны ортсысянь, налӧн ӧтувъя ортсыса касательнӧйыс эм диаметръяс костас средньӧй пропорциональнӧй. Докажитны.

78. ABCD трапецияын ичӧтджык BD диагональыс AD да BC подувтасъясыслы перпендикулярнӧй; A да C ёсь пельӧсъясыслӧн суммаыс 90° ыджда. Подувтасъяс: AD = a, BC = b. Определитны боквывса AB да CD бокъяссӧ.

Пӧлӧс пельӧса куимпельӧса.

79. 36 чертёж вылын мыччӧдӧма помещенньӧлысь плансӧ. Тайӧ помещенньӧсӧ кӧсйӧны юкны AC визь кузя. AC-ӧс муртавнысӧ оз позь, сы вӧсна, мый паныдасьӧны препятствийӧяс. Сы пыдди лои мурталӧма татшӧм визьяс: AB = 50 м, BC = 35 м да ∠ABC = 60°. Тайӧ сетӧмъяс кузя артавны AC.

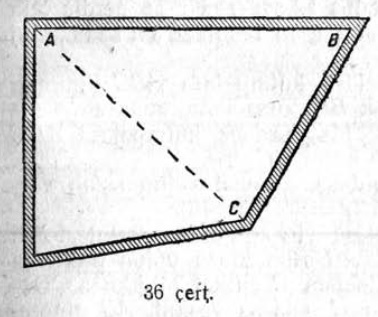
80. 37 чертёж вылын мыччӧдӧма кран, кодлӧн стойкаыс a = 10 м да плечоыс b = 13 м. a да b костын пельӧсыс 120° ыджда. Определитны C тягалысь кузьтасӧ.

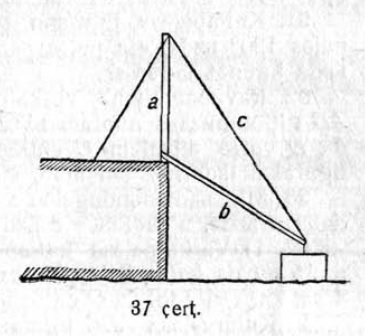
81. Куимпельӧсаын определитны боквывса мӧд боксӧ, кор боквывса первой бокыс, подувтасыс да подувтас вылӧ мӧд бокыслӧн проекцияыс соответственнӧя мыччӧдчӧны татшӧм лыдъясӧн: 1) 6; 5; 3,8; 2) 2; 3; 2; 3) 12; 8; 11; 4) 2; 2; 3.

82. Определитны куимпельӧсалысь сикассӧ (пельӧсъяс серти), сетӧма кӧ сылысь куимнан боксӧ либӧ налысь отношенньӧяссӧ: 1) 2; 3; 4. 2) 3 : 4 : 5. 3) 4; 5; 6. 4) 10 : 15 : 18. 5) 68; 119; 170.

83. ABC куимпельӧсаын медым лоӧны: b — подувтас, a да c — боквывса бокъяс; p да q — подувтас вылӧ налӧн проекцияяс, h — судта. Определитны p, q да h, сетӧма кӧ куимнан боксӧ:

1) a = 13, b = 14, c = 15; 2) a = 37, b = 30, c = 13; 3) a = 25, b = 12, c = 17; 4) a = 2, b = 4, c = 3.

84. Куимпельӧсаын определитны коймӧд боксӧ, мӧд кыкыс кӧ вӧчӧны 60°-а пельӧс да ыдждаясыс налӧн татшӧмӧсь: 1) 5 см да 8 см; 2) 8 см да 15 см; 3) 63 см да 80 см.

85. Куимпельӧсаын определитны коймӧд боксӧ, мӧд кыкыс кӧ вӧчӧны 120°‐а пельӧс да налӧн ыдждаясыс соответственнӧя татшӧмӧсь: 1) 3 см да 5 см; 2) 7 см да 8 см; 3) 11 см да 24 см.

86. Куимпельӧсаын определитны коймӧд боксӧ, мӧд кыкыс кӧ вӧчӧны 45°-а пельӧс да налӧн ыдждаясыс соответственнӧя татшӧмӧсь: 1) 2 да 3; 2) да 5; 3) да 7.

87. Определитны куимпельӧсалысь бокъяссӧ, кор тӧдам, мый ыджда сертиыс шӧр бокыс торъялӧ быд мӧд кык боксьыс 1 вылӧ да мый ыджыд бокыслӧн шӧр бокыс вылӧ проекцияыс 9 единича ыджда.

88. Куимпельӧсалӧн бокыс 21 см ыджда, а мӧд кык бокыс вӧчӧны 60°-а пельӧс да относитчӧны кыдз 3 : 8. Определитны тайӧ бокъяссӧ.

89. Куимпельӧсаын боквывса бокыс 16 м ыджда да подувтасыскӧд вӧчӧ 60°-а пельӧс; боквывса мӧд бокыс 14 м ыджда. Определитны подувтассӧ.

90. Куимпельӧсалӧн подувтасыс 13 см; йывбердса пельӧсыс 60°; боквывса бокъясыслӧн суммаыс 22 см. Определитны боквывса бокъяссӧ да судтасӧ.

91. Куимпельӧсаын подувтасыс 12 см ыджда; сы бердса пельӧсъяс пиысь ӧтиыс 120° ыджда; тайӧ пельӧслы воча бокыс 28 см ыджда. Определитны коймӧд боксӧ.

92. Кык ӧткузя бока веськыд пельӧса ABC куимпельӧсаын AB гипотенузасӧ нюжӧдӧма BC ыджда BD кузьтаӧдз; D чутсӧ ӧтлаалӧма C-кӧд. Определитны ADC куимпельӧсалысь бокъяссӧ, BC катет кӧ = a.

93. Определитны джынъя дугалысь хордасӧ, быдса дугалӧн кӧ хордаыс a ыджда да радиусыс r ыджда (r = 25; a = 48).

94. 1) Веськыд пельӧса ABC куимпельӧсаын AC катет = 15 см, BC катет = 20 см. AB гипотенуза вылӧ пуктӧма 4 см кузя AD юкӧн, D чутсӧ ӧтлаалӧма C-кӧд. Определитны CD-лысь кузьтасӧ.

2) ABC куимпельӧса — C бердын веськыд пельӧса. AB гипотенузаӧс нюжӧдӧм вылӧ пуктӧма BC катет ыджда BD вундӧг; D чутсӧ ӧтлаалӧма C-кӧд. Определитны CD-лысь кузьтасӧ, BC кӧ = 7 см да AC = 24 см.

95. ABC куимпельӧсаын нуӧдӧма BD да CE судтаяс да D да E чутъяссӧ ӧтлаалӧма. Корсьны ADE да ABC площадьяслысь отношенньӧсӧ: 1) ∠A кӧ = 45°; 2) ∠A кӧ = 30°.

96. ABC куимпельӧсаын AB бок вылас сетӧма D чут; определитны CD-лысь кузьтасӧ, тӧдам кӧ, мый a = 37; b = 15; c = 44 да AD = 14.

97. Тшӧтшыд пельӧса куимпельӧсаын медыджыд бокыс 16 см ыджда; сы помъясысь нуӧдӧм судтаясыс тшӧтшыд пельӧс йывсянь 2 см да 3 см сайынӧсь. Определитны мӧд кык ичӧтджык бокъяссӧ.

98. Кык ӧткузя бока куимпельӧсалӧн бокъясыс: AB = BC = 50 см да AC = 60 см. Нуӧдӧма AE да CD судтаяс да D да E чутъяссӧ ӧтлаалӧма. Определитны DBE куимпельӧсалысь бокъяссӧ.

99. ABC куимпельӧсаын AC бокса C помас сувтӧдӧма сылы перпендикуляр AB бок нюжӧдӧмкӧд D чутын вомӧнассьытӧдз. Определитны BD да CD, AB кӧ = 45, BC = 39 да AC = 42.

100. ABC куимпельӧсалысь сетӧма бокъяссӧ: AB = 15, AC = 14 да BC = 13. B пельӧсса биссектрисасӧ нюжӧдӧма йыв саяс AC-лы C чутын сувтӧдӧм перпендикуляркӧд E чутын вомӧнассьытӧдз. Определитны CE-лысь кузьтасӧ.

101. Сетӧм кругӧ касайтчӧны кык ӧтыджда ичӧтджык кругъяс — ӧтиыс пытшкӧссяньыс, а мӧдыс ортсысяньыс, та дырйи касанньӧ чутъяскостса дугаыс 60°. Ичӧтджык кругъясыслӧн радиусъясыс r ыдждаӧсь; ыджыд кругыслӧн радиусыс R ыджда. Определитны ичӧтджык кругъясса шӧр чутъяскостса расстоянньӧсӧ.

Параллелограмм да трапеция.

102. 1) Параллелограммлӧн бокъясыс 23 см да 11 см ыдждаӧсь, диагональясыс относитчӧны кыдз 2 : 3. Определитны диагональяссӧ.

2) Параллелограммлӧн диагональясыс 17 см да 19 см ыдждаӧсь да бокъясыс относитчӧны кыдз 2 : 3. Определитны бокъяссӧ.

103. 1) Параллелограммлӧн диагональясыс 12 см да 14 см ыдждаӧсь, бокъясыслӧн разносьтыс 4 см ыджда. Определитны параллелограммлысь бокъяссӧ.

2) Определитны параллелограммлысь бокъяссӧ да диагональяссӧ, ыджыдджык бокыс кӧ ичӧтджык диагональыс ыджда, бокъясыслӧн разносьтыс 3 см ыджда да диагональясыслӧн разносьтыс 2 см ыджда.

104. 1) Куимпельӧсалӧн бокъясыс: 16, 18 да 26. Артавны медыджыд бокыслысь медианасӧ.

2) Куимпельӧсалӧн кык бок 7 да 11; коймӧд бокас медианаыс 6 ыджда. Определитны коймӧд боксӧ.

3) Куимпельӧсалӧн бокъясыс a, b да c. Определитны медианаяссӧ.

105. Определитны параллелограммлысь судтасӧ, подувтасыс кӧ сылӧн 51 см, а диагональясыс 40 см да 74 см ыдждаӧсь.

106. Кык ӧткузя бока трапецияысь определитны диагональясыслысь кузьтаяссӧ: 1) подувтасъясыс кӧ 4 м да 6 м ыдждаӧсь, а боквывса бокыс 5 м ыджда; 2) ӧти бок кӧ 5 см ыджда да быд мукӧд куимыс 4 см ыдждаӧсь.

107. Определитны трапециялысь судтасӧ да диагональяссӧ, кор a да c подувтасъясыс да b да d боквывса бокъясыс выражайтчӧны татшӧм лыдъясӧн:

1) a = 25, b = 13, c = 11, d = 15;

2) a = 28, b = 25, c = 16, d = 17;

3) a = 6, b = 3, c = 1, d = 4.

108. Куимпельӧсаӧ впишитӧма параллелограмм сідз, мый сылӧн ӧти бокыс куйлӧ куимпельӧсаса подувтас вылас, а диагональясыс куимпельӧсаса боквывса бокъяслы соответственнӧ параллельнӧйӧсь. Куимпельӧсалӧн подувтасыс 45 см ыджда, а боквывса бокъясыс — 39 см да 48 см. Определитны параллелограммлысь бокъяссӧ.

109. Докажитны, мый кык ӧткузя бока трапецияын диагональыслӧн квадратыс равняйтчӧ боквывса бокыс квадратлы, подувтасъяслысь произведенньӧсӧ содтӧмӧн.

110. Докажитны, мый быд трапецияын диагональяслӧн квадратъяс равняйтчӧны боквывса бокъясыс квадратъяс суммалы, код дорӧ содтӧма подувтасъяслысь кыкпӧлалӧм произведенньӧ.

111. Докажитны, мый быд нёльпельӧсаын диагональяс квадратъяслӧн суммаыс воча бокъяслысь шӧръяссӧ ӧтлаалысь веськыдъяс квадратъяс суммаысь кык пӧв ыджыдджык.

112. Определитны ромблысь ёсь пельӧссӧ, кор ромбас бокыс эм диагональяс костас средньӧй пропорциональнӧй.

11 §. Кругын пропорциональнӧй вундӧгъяс.

1. Пос фермаӧс ограничитӧма кытшвизьса дуга (38 чертёж). Сылӧн судтаыс MK = h = 3 м, пролётса AMB дугалӧн радиусыс R = 8,5 м. Артавны послысь AB пролётсӧ.

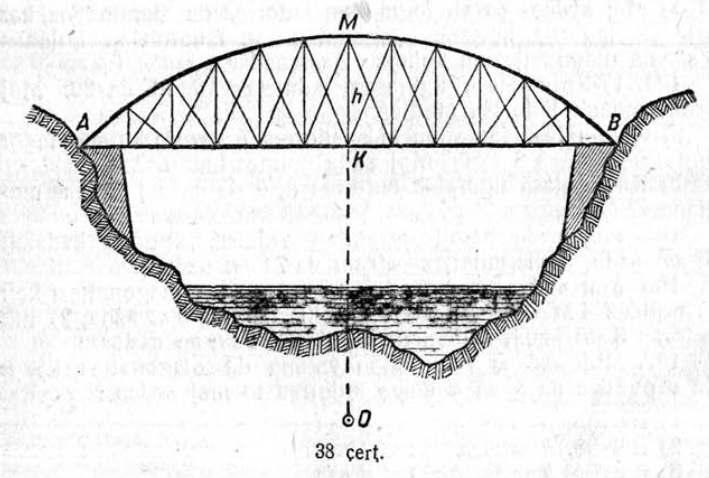
2. Цилиндр джын формаа свода пӧдвалын колӧ сувтӧдны кык стойка, медым быдӧн найӧ вӧліны ӧтылнаынӧсь медматыс стенсяньыс. Определитны стойкаясыслысь джудждасӧ, пӧдвалыслӧн кӧ увтіыс пасьтаыс 4 м да стойкаяс костыс 2 м.

3. 1) Кытшвизьвывса чутысь диаметр вылас лэдзӧма перпендикуляр. Определитны сылысь кузьтасӧ, кор диаметрыслӧн вундӧгъясыс татшӧмӧсь: 1) 12 см да 3 см; 2) 16 см да 9 см; 3) 2 м да 5 дм.

2) Диаметрвывса чутысь сувтӧдӧма кытшвизькӧд вомӧнассьытӧдз перпендикуляр. Определитны тайӧ перпендикулярлысь кузьтасӧ, диаметрыс кӧ 40 см да диаметр ӧти помсяньыс перпендикулярӧдзыс 8 см.

4. Диаметрӧс юкӧма вундӧгъясӧ: AC = 8 дм да CB = 5 м, C чутысь сувтӧдӧма сетӧм кузьтаа CD перпендикуляр. Индыны D чутлысь кытшвизь серти положенньӧсӧ, кор CD 1) 15 дм; 2) 2 м; 3) 23 дм ыджда.

5. ACB — кытшвизь джын; CD лоӧ AB диаметр вылӧ перпендикуляр. Колӧ:

1) определитны DB, AD кӧ = 25 да CD = 10;

2) определитны AB, кор AD : DB = 4 : 9 да CD = 30;

3) определитны AD, кор CD = 3AD, а радиус = r.

4) определитны AD, кор AB = 50 да CD = 15.

6. 1) 34 см ыджда радиус вылӧ кытшвизьвывса чутысь лэдзӧм перпендикуляр юкӧ радиуссӧ (шӧр чутсянь пондӧмӧн) 8 : 9 отношенньӧын. Определитны перпендикулярлысь кузьтасӧ.

2) BDC хорда ODA радиуслы перпендикулярнӧй. Определитны BC, OA кӧ = 25 см да AD = 10 см.

3) Кык концентрическӧй кытшвизьысь артмӧм концентрическӧй кольцолӧн пасьтаыс 8 дм; ыджыдджык кытшвизьыслӧн хордаыс ичӧтджыкас касайтчӧ да 4 м ыджда. Определитны кытшвизьясыслысь радиусъяссӧ.

7. Вундӧгъясӧс сравнивайтӧмӧн докажитны, мый кык (абу ӧтыджда) лыдлӧн средньӧй арифметическӧйыс на костса средньӧй геометрическӧйысь ыджыдджык.

8. Вӧчны 3 см да 5 см кузя вундӧгъяскостса средньӧй пропорциональнӧй вундӧг.

9. Вӧчны ыджда вундӧгъяс.

10. ADB — диаметр; AC — хорда; CD — диаметр вылӧ перпендикуляр. Определитны AC хорда: 1) AB кӧ = 2 м да AD = 0,5 м; 2) AD кӧ = 4 см да DB = 5 см; 3) AB кӧ = 20 м да DB = 15 м.

11. AB — диаметр; AC — хорда; AD — сылӧн AB диаметр вылӧ проекция. Колӧ:

1) определитны AD, AB кӧ = 18 см да AC = 12 см;

2) определитны радиус, AC кӧ = 12 м да AD = 4 м;

3) определитны DB, AC кӧ = 24 см да DB = 7⁄9AD.

12. AB — диаметр; AC — хорда; AD — сылӧн AB диаметр вылӧ проекция. Колӧ:

1) определитны AC, AB кӧ = 35 см да AC = 5AD;

2) определитны AC, радиус кӧ = r да AC = DB.

13. Кык хорда вомӧнассьӧны круг пытшкын. Ӧти хордаыслӧн вундӧгъясыс — 24 см да 14 см; мӧд хордаыслӧн ӧти вундӧгыс 28 см ыджда. Определитны сылысь мӧд вундӧгсӧ.

14. Пос ферма — кытшвизь дуга формаа (38 чертёж); кузьтаыс послӧн: AB = 6 м, судтаыс: h = 1,2 м. Определитны дугаыслысь радиуссӧ (OM = R).

15. AB да CD кык вундӧг вомӧнассьӧны M чутын сідз, мый MA = 7 см, MB = 21 см, MC = 3 см да MD = 16 см. Куйлӧны-ӧ A, B, C да D чутъяс ӧти кытшвизь вылын?

16. Маятниклӧн кузьтаыс: MA = l = 1 м (39 чертёж), а пельӧс вылӧ отклонитчигӧн сы лыбӧмлӧн судтаыс CA = h = 10 см. Корсьны MA-сянь B чутӧдз BC колассӧ, мӧдног кӧ, BC = x.

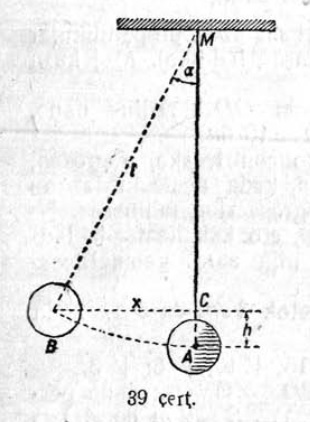
17. b = 1,524 м пасьтаа кӧрт туйӧс кежӧдӧм вылӧ AB местаын вӧчӧма закругленньӧ (40 чертёж); та дырйи BC = a = 42,4 м. Определитны закругленньӧыслысь OA = R радиуссӧ.

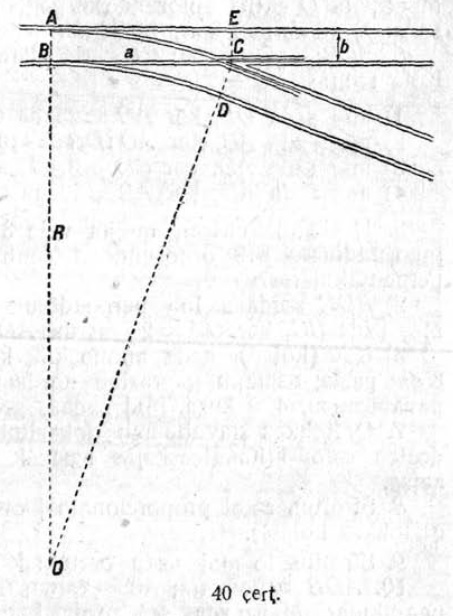
18. AMB хордаӧс M чут гӧгӧр бергӧдӧма сідз, мый MA вундӧгыс ыдждіс 2½ пӧв. Кыдз вежсис MB вундӧг?

19. 1) Кык вомӧнассян хорда пиысь ӧтиыс юксис 48 см да 3 см кузя вундӧгъясӧ, а мӧдыс — шӧри. Определитны мӧд хордаыслысь кузьтасӧ.

2) Кык вомӧнассян хордаяс пиысь ӧтиыс юксис 12 м да 18 м кузя вундӧгъясӧ, а мӧдыс — 3 : 8 отношенньӧын. Определитны мӧд хордаыслысь кузьтасӧ.

20. Кык вомӧнассян хорда пиысь ӧтиыс 32 см ыджда, а мӧдыслӧн вундӧгъясыс — 12 см да 16 см. Определитны первой хордаыслысь вундӧгъяссӧ.

21. ABC вундысьӧс ортсыса A чут гӧгӧр бергӧдӧма сідз, мый ортсыса AB вундӧгыс ичӧтмис 3 пӧв. Кыдз вежсис вундысьлӧн кузьтаыс?

22. ADB да AEC — кытшвизьӧс вомӧналысь кык веськыд визь, та дырйи первойыс сійӧс вомӧналӧ D да B чутъясын, а мӧдыс — E да C чутъясын. Колӧ:

1) определитны AE, AD кӧ = 5 см, DB = 15 см да AC = 25 см;

2) определитны BD, AB кӧ = 24 м, AC = 16 м да EC = 10 м;

3) определитны AB да AC, AB + AC кӧ = 50 м да AD : AE = 3 : 7.

23. Кытшвизьлӧн радиусыс 7 см ыджда. Шӧр чутсянь 9 см сайса чутысь нуӧдӧма вундысьӧс сідз, мый сійӧ кытшвизьнас юксьӧ шӧри. Определитны тайӧ вундысьлысь кузьтасӧ.

24. MAB да MCD — ӧти кытшвизьӧс вундысьяс. Колӧ:

1) определитны CD, MB кӧ = 1 м, MD = 15 дм да CD = MA;

2) определитны MD, MA кӧ = 18 см, AB = 12 см да MC : CD = 5 : 7;

3) определитны AB, AB кӧ = MC, MA = 20 да CD = 11.

25. Кык хордаӧс нюжӧдӧма мӧда-мӧдыскӧд вомӧнассьытӧдз. Определитны артмӧм нюжӧдӧмъясыслысь кузьтаяссӧ, хордаяс кӧ a да b ыдждаӧсь да найӧс нюжӧдӧмъясыс относитчӧны кыдз m : n.

26. Ӧти чутысь кытшвизь бердӧ нуӧдӧма вундысьӧс да касательнӧйӧс. Определитны касательнӧйыслысь кузьтасӧ, вундысьыслӧн кӧ ортсыса да пытшкӧс вундӧгъясыс соответственнӧя пасйыссьӧны лыдъясӧн: 1) 4 да 5; 2) 2,25 да 1,75; 3) 1 да 2.

27. Касательнӧй 20 см ыджда, а сійӧ жӧ чутысь нуӧдӧм медыджыд вундысьыс 50 см ыджда. Определитны круглысь радиуссӧ.

28. Вундысь ас ортсыса вундӧгсьыс 2¼ пӧв ыджыдджык. Кымын пӧв сійӧ ыджыдджык сійӧ жӧ чутысь нуӧдӧм касательнӧйысь?

29. Кык вомӧнассьысь кытшвизьлысь ӧтувъя хордасӧ нюжӧдӧма да нюжӧдӧм вылас босьтӧма кутшӧмкӧ чут, сысянь нуӧдӧма кытшвизьясӧ касательнӧйясӧс. Докажитны, мый найӧ ӧтыдждаӧсь.

30. ∠A ӧти бок кузяыс пукталӧма мӧда-мӧд бӧрсяыс вундӧгъясӧс: AB = 6 см да BC = 8 см; мӧд бок вылас пуктӧма вундӧг AD = 10 см. B, C да D чутъяс пырыс нуӧдӧма кытшвизь. Тӧдмавны, касайтчӧ-ӧ тайӧ кытшвизьӧ AD веськыд, оз кӧ, A-сянь кымынӧд вомӧнассянін чутӧн лоӧ D чутыс.

31. AB — касательнӧй да ACD — сійӧ жӧ кытшвизьӧ вундысь. Колӧ:

1) определитны CD, AB кӧ = 2 см да AD = 4 см;

2) определитны AD, AC : CD кӧ = 4 : 5 да AB = 12 см;

3) определитны AB, AB кӧ = CD да AC = a.

32. 1) Ылӧ-ӧ тыдалӧ 4 км вылнаӧ кайӧм воздушнӧй шарсянь (мулӧн радиусыс 6370 км)?

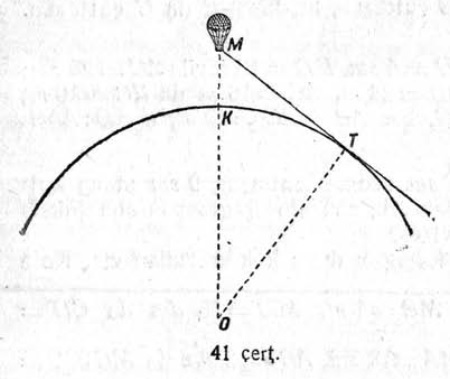
2) Кавказын Эльбрус гӧра море уровеньсянь 5600 м джуджда. Ылӧ-ӧ позьӧ аддзыны тайӧ гӧра йывсяньыс?

3) M — му вывсянь h метр джуджда наблюдательнӧй пункт (42 чертёж); мулӧн радиусыс = R; MT = d — медыджыд тыдалан расстоянньӧ. Докажитны, мый

Индӧд. Сы вӧсна мый h² величинаыс 2Rh дорын зэв ичӧт, унджыкысь пӧльзуйтчӧны матыстӧм формулаӧн:

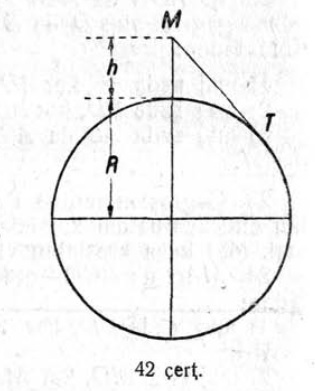
33. 1) Ӧти чутысь петысь касательнӧй да вундысь 20 см да 40 см ыдждаӧсь; вундысьӧдз шӧр чутсянь 8 см. Определитны круглысь радиуссӧ.

2) Определитны расстоянньӧсӧ шӧр чутсянь сійӧ чутӧдз, кытысь петӧны касательнӧй да вундысь, найӧ кӧ соответственнӧя 4 см да 8 см ыдждаӧсь да вундысьӧдз шӧр чутсянь 12 см.

34. 1) Ӧтувъя чутысь нуӧдӧма касательнӧйӧс да вундысьӧсь. Определитны касательнӧйлысь кузьтасӧ, сійӧ кӧ 5 см-ӧн вундысь ортсыса вундӧгсьыс ыджыдджык да сы мындаӧн жӧ пытшкӧс вундӧгсьыс ичӧтджык.

2) Кытшвизьӧ ӧтувъя чутысь нуӧдӧма касательнӧйӧс да вундысьӧс. Вундысьыс a ыджда да сылӧн пытшкӧс вундӧгыс ортсыса вундӧгсьыс касательнӧй кузьтаӧн ыджыдджык. Определитны касательнӧйсӧ.

35. Кытшвизьӧ ӧти чутысь нуӧдӧма касательнӧй да вундысьӧс. Касательнӧйыс ыджыдджык вундысь вундӧгъяссьыс — пытшкӧссьыс 2 см-ӧн, а ортсысасьыс 4 см-ӧн. Определитны вундысьлысь кузьтасӧ.

36. Кытшвизьӧ ӧти чутысь нуӧдӧма касательнӧйӧс да вундысьӧс. Определитны налысь кузьтаяссӧ, касательнӧйыс кӧ 20 см-ӧн вундысь пытшкӧс вундӧгсьыс ичӧтджык да 8 см-ӧн ортсыса вундӧгсьыс ыджыдджык.

37. 1) Кытшвизьӧ ӧти чутысь нуӧдӧма вундысьӧс да касательнӧйӧс. Налӧн суммаыс 30 см ыджда да вундысьлӧн пытшкӧс вундӧгыс касательнӧйсьыс 2 см-ӧн ичӧтджык. Определитны вундысьсӧ да касательнӧйсӧ.

2) Кытшвизьӧ ӧти чутысь нуӧдӧма вундысьӧс да касательнӧйӧс. Налӧн суммаыс 15 см да вундысьлӧн ортсыс вундӧгыс касательнӧйсьыс 2 см-ӧн ичӧтджык. Определитны вундысьсӧ да касательнӧйсӧ.

38. AB вундӧгӧс нюжӧдӧма BC расстоянньӧ вылӧ. AB да AC вылӧ кыдз диаметръяс вылӧ вӧчӧма кытшвизьяс. AC вундӧглы B чутын сувтӧдӧма BD перпендикуляр ыджыдджык кытшвизьыскӧд вомӧнассьытӧдз. C чутсьыс нуӧдӧма ичӧтджык кытшвизяс CK касательнӧйӧс. Докажитны, мый CD = CK.

39. Сетӧм кытшвизьӧ нуӧдӧма кык параллельнӧй касательнӧй да найӧс вомӧналысь коймӧд касательнӧй. Докажитны, мый радиусыс лоӧ коймӧд касательнӧйса вундӧгъяс костас средньӧй пропорциональнӧйӧн.

40. Сетӧма кык параллельнӧй веськыдӧс, ӧтисянь мӧдӧдзыс 15 дм; на костын сетӧма ӧтисяньыс 3 дм сайын M чут. M чут пыр нуӧдӧма кытшвизь, коді касайтчӧ кыкнан параллеляс. Определитны сетӧм параллельяс пиысь ӧтиыс вылӧ шӧр чут да M чут проекцияяскостса расстоянньӧсӧ.

41. r радиуса кругӧ впишитӧма кык ӧткузя бока куимпельӧсаӧс, кодлӧн подувтасыслӧн да судтаыслӧн суммаыс круг диаметрыс ыджда. Определитны судтасӧ.

42. Кык ӧткузя бока куимпельӧса гӧгӧр опишитӧм круглысь определитны радиуссӧ: 1) подувтасыс кӧ 16 см ыджда, а судтаыс — 4 см; 2) боквывса бокыс кӧ 12 дм ыджда, а судтаыс — 9 дм; 3) боквывса бокыс кӧ 15 м ыджда, а подувтасыс — 18 м.

43. Кык ӧткузя бока куимпельӧсаын подувтасыс 48 дм ыджда, а боквывса бокыс — 30 дм. Определитны описаннӧй да вписаннӧй кругъяслысь радиусъяссӧ да шӧр чутъяскостса расстоянньӧсӧ.

44. Радиус r ыджда, сетӧм дугалӧн хордаыс a ыджда. Определитны кыкпӧлалӧм дугалысь хордасӧ.

45. Кытшвизьлӧн радиусыс 8 дм; AB хорда 12 дм. A чут пыр нуӧдӧма касательнӧйӧс, B чутысь нуӧдӧма касательнӧйлы параллельнӧй BC хорда. Определитны BC хордасянь касательнӧйӧдзыс расстоянньӧсӧ.

46. A чутӧс MN веськыдсянь ылысмӧдӧма a расстоянньӧ ылнаӧ. Сетӧм r радиусӧн нуӧдӧма кытшвизь сідз, мый сійӧ мунӧ A чут пыр да касайтчӧ MN визьӧ. Определитны сетӧм А чутсянь артмӧм касанньӧ чутӧдз расстоянньӧсӧ.

12 §. Правильнӧй унапельӧсаяс.

Пасйӧмъяс. n — правильнӧй унапельӧсалӧн бок лыдыс; aₙ — правильнӧй вписаннӧй унапельӧсалӧн бокыс, bₙ — правильнӧй описаннӧй унапельӧсалӧн бокыс, kₙ — правильнӧй вписаннӧй унапельӧсалӧн апофемаыс; R — описаннӧй кытшвизьлӧн радиусыс; r — вписаннӧй кытшвизьлӧн радиусыс.

1. 1) Артавны центральнӧй пельӧссӧ правильнӧй 24‐пельӧсалысь да 16‐пельӧсалысь.

2) Кутшӧм правильнӧй унапельӧсалӧн центральнӧй пельӧсыс 30° ыджда? 12° ыджда?

2. Правильнӧй унапельӧсаын центральнӧй пельӧсыс да йывбердса пельӧсыс суммаын сетӧны 180°. Докажитны.

3. Определитны правильнӧй n-пельӧсалысь пельӧслысь ыдждасӧ (n = 3; 4; 5; 6; 8; 10; 12; 25).

4. 1) Кымын бок правильнӧй унапельӧсаын, кодлӧн пытшкӧс пельӧсыс 135° ыджда? 150° ыджда?

2) Кымын бок правильнӧй унапельӧсаын, кодлӧн ортсыса пельӧсыс 36° ыджда? 24° ыджда?

5. 4 см диаметра валик помӧс шыльӧдӧма квадрат кодя. Определитны медыджыд размер, коді вермас лоны квадрат боклӧн.

6. Газӧвӧй задвижка винтлӧн помыс куим грана правильнӧй формаа. Кутшӧм медыджыд размера вермас лоны граныс, винтыслӧн кӧ цилиндрическӧй юкӧныс 2 см ыджда диаметра?

7. Артавны, кутшӧм размера колӧ лоны квайт грана правильнӧй гайкалы ключлӧн w коластыс, гайка граныслӧн кӧ пасьтаыс a₆ — 2,5 см. Гайка гран да ключ костӧ кольсьӧ 0,5 мм ыджда колас (43 черт.).

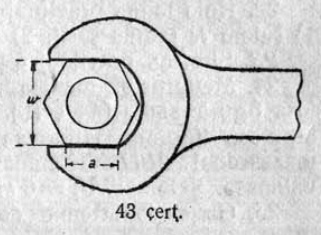
8. 1) Кытшвизьӧ впишитны правильнӧй 12-пельӧсаӧс, 15-пельӧсаӧс.

2) Круг гӧгӧр опишитны правильнӧй 8‐пельӧсаӧс, 10‐пельӧсаӧс.

3) Сетӧм a бок серти вӧчны правильнӧй 8-пельӧсаӧс, 12‐пельӧсаӧс.

9. 1) Хорда, коді радиуслы шӧрас перпендикулярнӧй, правильнӧй вписаннӧй куимпельӧса бок ыджда. Докажитны.

2) Петкӧдлыны, мый k₆ = 0,5a₃.

10. 1) Правильнӧй куимпельӧсаын апофемаыс ⅓ судтаыс да описаннӧй круг ½ радиусыс ыджда. Докажитны.

2) Правильнӧй куимпельӧса гӧгӧр опишитӧм кытшвизьлӧн да сы пытшкӧ впишитӧм кытшвизьлӧн радиусъяс костас разносьтыс m ыджда. Определитны куимпельӧсалысь боксӧ.

11. 1) Правильнӧй унапельӧсалӧн бокыс a ыджда; тайӧ унапельӧса гӧгӧр опишитӧм круглӧн радиусыс R ыджда. Определитны вписаннӧй круглысь радиуссӧ.

2) Правильнӧй унапельӧсалӧн бокыс a ыджда; сыӧ впишитӧм круглӧн радиусыс r ыджда. Определитны описаннӧй круглысь радиуссӧ.

3) R — правильнӧй унапельӧса гӧгӧр опишитӧм круглӧн радиусыс; r — вписаннӧй круглӧн радиусыс. Определитны тайӧ унапельӧсалысь боксӧ.

12. R = 4 см радиуса кытшвизьӧ впишитӧма правильнӧй 6-пельӧса. Корсьны бокъясыслысь быд диагональ вылӧ проекцияяссӧ.

13. Докажитны, мый

1)

2)

14. Докажитны, мый

1)

2)

15. Сетӧм a серти определитны R, кор n: 1) 3; 2) 4; 3) 6; 4) 8; 5) 12.

16. Сетӧм a серти определитны 1) k₃; 2) k₄; 3) k₆.

17. Сетӧм k серти определитны R, кор n: 1) 3; 2) 4; 3) 6; 4) 8.

18. Сетӧм R серти определитны 1) b₃; 2) b₄; 3) b₆.

19. Правильнӧй вписаннӧй n‐пельӧсаса сетӧм a бок серти да кытшлӧн R радиус серти^Вуджӧдӧмын R йылысь абу гижӧма. — А.В./^ определитны правильнӧй описаннӧй n-пельӧсалысь b боксӧ.

20. R = 50 см радиуса кругӧ впишитны правильнӧй 7-пельӧсаӧс сійӧн пӧльзуйтчӧмӧн, мый правильнӧй вписаннӧй 7-пельӧсалӧн бокыс правильнӧй вписаннӧй куимпельӧсаса бок джын ыджда (матыстӧмӧн).

21. Определитны правильнӧй 8-пельӧсалысь диагональяссӧ: 1) сетӧм R серти; 2) сетӧм a бок серти.

22. Определитны правильнӧй 12-пельӧсаын диагональяслысь кузьтасӧ 1) сетӧм R радиус серти; 2) сетӧм a бок серти.

23. Вӧчны правильнӧй 5-пельӧсаӧс диагональ серти.

24. Медпрӧстӧй мансарднӧй вевт вертикальнӧй вундӧмын вӧчӧ правильнӧй 8-пельӧсалысь джынсӧ (44 чертёж). Корсьӧй вевттьӧмлысь BD пасьтасӧ, 8-пельӧсалысь быд боксӧ да ABDE мансарднӧй комнаталысь джудждасӧ. Сетӧма: AE = 6 м.

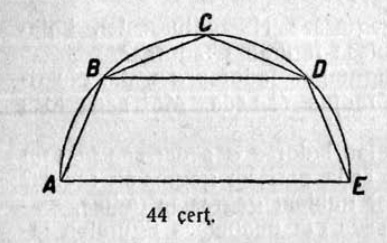
25. Кытшвизьӧ впишитӧма да сы гӧгӧр опишитӧма правильнӧй n-пельӧсаяс. Корсьны тайӧ n-пельӧсаясса бокъяслысь отношенньӧсӧ (n = 3; n = 6).

26. R радиуса кытшвизьӧ впишитӧма правильнӧй n-пельӧсаӧс да бокъясыслысь шӧръяссӧ водзысь водзӧ ӧтлаалӧма. Определитны выль n-пельӧсалысь боксӧ, n кӧ: 1) 6; 2) 8.

27. Правильнӧй a бока 8-пельӧсаын ӧтлаалӧма 4 бокъяслысь шӧръяссӧ (быд ӧти бокӧс ордйӧмӧн) сідз, мый артмӧма квадрат. Определитны квадратыслысь боксӧ.

2) a бока правильнӧй 12 пельӧсаын ӧтлаалӧма 6 бокъяслысь шӧръяссӧ быд ӧти бокӧс ордйӧмӧн сідз, мый артмӧма правильнӧй 6-пельӧса. Определитны сылысь боксӧ.

28. Вӧчны правильнӧй 8-пельӧсаӧс сетӧм квадратлысь пельӧсъяссӧ орйӧдлӧмӧн.

Медым сетӧм квадратӧс (пельӧсъяссӧ орлалӧмӧн) пӧртны правильнӧй 8-пельӧсаӧ, колӧ сылысь бокъяссӧ вундавны квадратса диагональ джын ыджда радиуса дугаясӧн, кодъяслӧн шӧр чутъясыс квадрат йывъясас. Докажитны, мый артмӧм 8-пельӧсаыс правильнӧй.

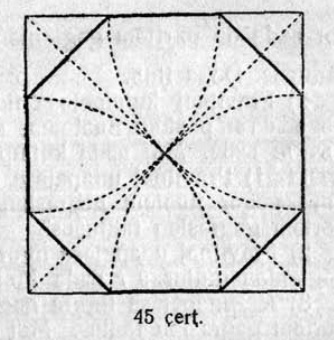
29. a бока сетӧм правильнӧй куимпельӧсаӧс пельӧсъяссӧ орйӧдлӧмӧн пӧртны правильнӧй 6‐пельӧсаӧ да определитны сылысь боксӧ.

30. R радиуса кытшвизьӧ впишитӧма aₙ бока правильнӧй унапельӧсаӧс. Тайӧ унапельӧсалысь бокъяс лыдсӧ кыкпӧлавны да докажитны, мый

31. Кытшвизьӧ впишитӧм правильнӧй куимпельӧсалӧн бокыс b ыджда. Корсьны круглысь радиуссӧ да кытшвизьӧ впишитӧм квадратлысь боксӧ.

32. 4 дм радиуса кытшвизьӧ впишитӧма правильнӧй куимпельӧсаӧс, сы бок вылӧ вӧчӧма квадрат. Определитны квадратыс гӧгӧр опишитӧм кытшвизьлысь радиуссӧ.

33. 1) R радиуса кытшвизьӧ впишитӧма правильнӧй куимпельӧсаӧс, кытчӧ впишитӧма круг, а тайӧ кругас впишитӧма квадрат. Определитны квадратлысь боксӧ.

2) a бока правильнӧй куимпельӧса гӧгӧр опишитӧма кытшвизь; тайӧ кытшвизьыс гӧгӧр опишитӧма квадрат; квадрат гӧгӧрыс — кытшвизь. Определитны квадрат гӧгӧр опишитӧм кытшвизьлысь радиуссӧ.

34. 1) Вомӧнассян кык кытшвизьлӧн ӧтувъя хордаыс a ыджда да лоӧ ӧти кытшвизяс впишитӧм правильнӧй куимпельӧсалӧн бокӧн, а мӧдас — впишитӧм квадратлӧн бокӧн. Определитны шӧр чутъяскостса расстоянньӧсӧ.

2) Вомӧнассян кык кытшвизьлӧн шӧр чутъясыс куйлӧны a кузя ӧтувъя хорданыс ӧтарбокын; хордаыс ӧти кытшвизьсьыс вундӧ 60° дуга, а мӧдсьыс — 30°-ӧс. Определитны шӧр чутъяскостса расстоянньӧсӧ.

35. ABC — правильнӧй вписаннӧй куимпельӧса; AD лоӧ AB боклӧн коймӧд юкӧн; BE лоӧ BC боклӧн коймӧд юкӧныс. Докажитны, мый DE визь — радиусыс ыджда.

36. a бока правильнӧй куимпельӧсалысь быд боксӧ юкӧма 3 ӧтыджда юкӧнӧ да соответственнӧй юкан чутъяссӧ (ӧти направленньӧӧн лыддьӧмӧн) ӧтлаалӧма, мый вӧсна лои выль куимпельӧса. Определитны сыӧ впишитӧм круглысь радиуссӧ.

37. Сетӧм квадратӧ впишитны мӧд квадратӧс, кодлысь боксӧ сетӧма. Век-ӧ тайӧ задача вермана?

38. Ромбӧ впишитны квадрат, кодлӧн бокъясыс медым вӧліны ромб диагональясыслы параллельнӧйӧсь.

39. a бока мӧда-мӧдыс вылӧ пуктӧм кык квадрат пиысь ӧтисӧ шӧр чут гӧгӧрыс бергӧдісны 45° улӧ. Определитны та дырйи артмӧм звездалысь периметрсӧ.

40. 1) Докажитны, мый правильнӧй 5-пельӧсалӧн диагональясыс вӧчӧны сідзжӧ правильнӧй 5-пельӧсаӧс.

2) Правильнӧй 5-пельӧсалысь кӧ бокъяссӧ нюжӧдам мӧда-мӧдыскӧд вомӧнасьтӧдз, артмӧ ӧтыджда бокъяса 5-пельӧса звезда (пентаграмма). Докажитны.

41. 1) R радиуса кытшвизьӧс юкӧма 6 ӧтыджда юкӧнӧ да юкан чутъяссӧ быд бӧрын ӧтиӧс кольӧмӧн йитлӧма хордаясӧн. Определитны артман 6-пельӧса звездалысь боксӧ.

2) R радиуса кытшвизьӧс юкӧма 8 ӧтыджда юкӧнъясӧ да юкан чутъяссӧ быд бӧрын ӧтиӧс кольӧмӧн йитлӧма хордаясӧн. Определитны 8-пельӧса звездалысь боксӧ.

42. Сетӧм R радиус серти определитны 1) 135°-а, 2) 150°-а дугалысь хордасӧ.

43. Определитны куимпельӧса бокъяслысь отношенньӧсӧ, пельӧсъясыс кӧ сылӧн относитчӧны кыдз 1 : 2 : 3.

44. Кытшвизь джынлысь шӧрсӧ ӧтлаалӧма диаметр помъясыскӧд да ӧтлаалысь вундӧгъяс шӧръяс пырыс нуӧдӧма хорда, кодлӧн бокса быд вундӧгыс c ыджда. Определитны круглысь радиуссӧ.

45. 120°а да h судтаа сегментӧ впишитӧма веськыднёльпельӧсаӧс, кодлӧн подувтасыс 4 пӧв ыджыдджык судтасьыс. Определитны веськыднёльпельӧсалысь судтасӧ.

46. R радиуса сетӧм кругӧ касайтчӧны ӧтыджда n кругъяс, кодъяс сідзжӧ касайтчӧны мӧда-мӧдыскӧд. Определитны тайӧ кругъяслысь радиуссӧ, налӧн кӧ n лыдыс: 1) 3; 2) 4; 3) 6.

47. Сетӧма вундӧг, сійӧс юкӧма шӧри, кыкнан джын вылас кыдз диаметръяс вылын вӧчӧма кругъяс, сетӧм вундӧг помъяссянь нуӧдӧма касательнӧйясӧс мӧд джын вылас вӧчӧм кытшвизьясӧ. Докажитны, мый касательнӧйяслысь вомӧнассянін чутъяссӧ ӧтлаалысь вундӧг лоӧ квадрат боккӧд ӧтыджда, кодӧс впишитӧма ӧти вӧчӧм кругӧ.

13 §. Веськыд визя фигураяслӧн площадьяс.

Квадрат.

1. Артавны туй трубалысь сеченньӧ площадьсӧ (мыччӧдӧма 46 чертёж вылын; размеръяссӧ сетӧма метръясӧн).

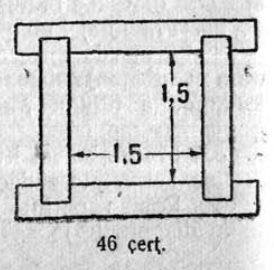
2. 1 мм² сеченньӧа кӧрт стержень орӧ 40 кг-а грузӧн. Кутшӧм грузӧн орӧ кӧрт стержень, кодлӧн вомӧна сеченньӧыс 24 мм бока квадрат?

3. Квадрат формаа кык му участоклӧн бокъясыс 100 м да 150 м. Определитны кыкнаныскӧд ӧтыджда (равновеликӧй) квадратнӧй му участоклысь боксӧ.

4. 1) Определитны квадратлысь площадьсӧ l диагональыс серти.

2) Определитны квадратлысь площадьсӧ, кодӧс впишитӧма R радиуса кругӧ.

3) Кымын пӧв описаннӧй квадратлӧн площадьыс ыджыдджык сійӧ жӧ кругӧ впишитӧм квадрат площадьысь?

5. 1) Кыдз вежсяс квадратлӧн площадьыс, боксӧ кӧ сылысь ыдждӧдны 3 пӧв? ичӧтмӧдны 1,5 пӧв?

2) Кыдз колӧ вежны квадратлысь боксӧ, медым площадьыс сылӧн ыдждас 4 пӧв? ичӧтмас 25 пӧв?

6. Квадратнӧй му участок планлӧн площадьыс 552,25 см² (масштаб 1 : 10000). Корсьны участоклысь действительнӧй площадьсӧ.

Веськыднёльпельӧса.

7. M типа „Рено“ танк веситӧ 6880 кг, сылӧн гусеничаясыслӧн пасьтаыс 0,35 м, быд гусенича (быд боксяньыс) муӧ инмӧ 2,05 м кузяӧ. Кутшӧм сьӧкта воӧ 1 дм² гусеничаса уджалан юкӧн площадь вылӧ?

8. Веськыднёльпельӧса формаа заводскӧй зданньӧлӧн кузьтаыс 82,5 м, пасьтаыс 26,5 м. Определитны аръясӧн зданньӧыслысь площадьсӧ.

9. Веськыднёльпельӧса му участокын 400 га, участоклӧн кузьтаыс 8 км; корсьны участок граничалысь кузьтасӧ (периметрсӧ).

10. 1) Определитны веськыднёльпельӧсалысь бокъяссӧ, найӧ кӧ относитчӧны кыдз 4 : 9, а площадьыс 144 м² ыджда.

2) Определитны веськыднёльпельӧсалысь бокъяссӧ, периметрыс кӧ сылӧн 74 дм да площадьыс 3 м².

11. Веськыднёльпельӧсалӧн бокъясыс 72 м да 8 м. Определитны сыкӧд ӧтыджда (равновеликӧй) квадратлысь боксӧ.

12. Ӧткодь бокъяса пельӧса кӧртлысь артавны вомӧна сеченньӧ площадьсӧ (47 чертёж ыдждасӧ петкӧдлӧма миллиметръясӧн).

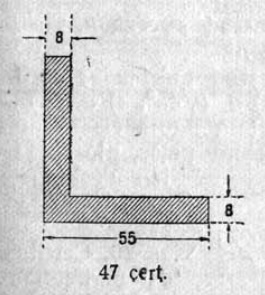
13. 48ʼ чертёжвывса трубалысь артавны вомӧна сеченньӧ площадьсӧ (размеръяссӧ сетӧма миллиметръясӧн).

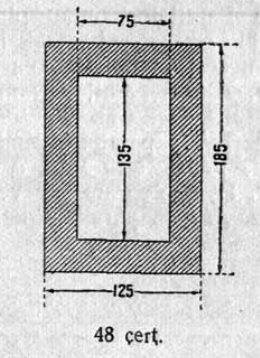
14. Веськыднёльпельӧсалӧн диагональыс 305 см, а площадьыс 37128 см². Определитны сылысь периметрсӧ.

Параллелограмм.

15. ABCD веськыднёльпельӧса формаа му вывті колӧ мунны кӧрт туйлы (49 чертёж). Тӧдам, мый AB = 125 м, BC = 72,5 м, AL = KC = 114,6 м. Артавны торйӧдан BLDK полосаыслысь площадьсӧ.

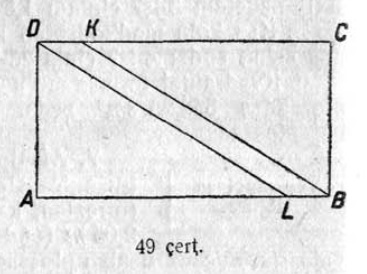
16. Параллелограммлӧн площадьыс = 480 см², периметрыс = 112 см; ыджыд бокъяскостса расстоянньӧыс 12 см. Определитны дзоля бокъяскостса расстоянньӧсӧ.

17. Определитны параллелограммлысь площадьсӧ кык судтаыс серти: h₁ да h₂ да 2p периметрыс серти.

18. Определитны параллелограммлысь площадьсӧ кык бок да на костса пельӧс серти: 1) а, b, 30°; 2) а, b, 45°; 3) а, b, 60°.

19. Параллелограммлӧн да веськыднёльпельӧсалӧн бокъясыс ӧткодьӧсь. Корсьны параллелограммлысь ёсь пельӧссӧ, площадьыс кӧ сылӧн веськыднёльпельӧсаса площадь джын ыджда.

20. Вӧчны квадрат да ромб, кодъяслӧн периметръясыс ӧтыдждаӧсь. Код фигураыслӧн площадьыс ыджыдджык? Мый вӧсна?

21. Определитны ромблысь площадьсӧ, сылӧн кӧ судтаыс = 12 см, а ичӧтджык диагональыс = 13 см.

22. ABCD параллелограмын AB бокыс = 37 м, диагональясыслӧн вомӧнассянін чутсяньыс AD бок вылас лэдзӧм перпендикуляр юкӧ сійӧс вундӧгъясӧ: AE = 26 м да ED = 14 м. Определитны параллелограмлысь площадьсӧ.

23. 1) ABCD параллелограмын (50 чертёж) нуӧдӧма AC диагональ да сы вылын босьтӧма произвольнӧй M чут. M чут пырыс нуӧдӧма параллелограмм бокъясыслы параллельнӧй веськыд визьяс: EF ∥ BC да GN ∥ CD. Докажитны, мый та дырйи артмӧм DHMF да EBGM параллелограмъяс, кодъяс пыр AC диагональыс оз мун, ӧтгырсяӧсь.

2) a = 8 см да b = 4 см бокъяса параллелограммӧс пӧртны сыкӧд ӧтгырся параллелограммӧ, кодлӧн медым вӧлі сэтшӧм жӧ пельӧс да b = 6 см ыджда подувтас.

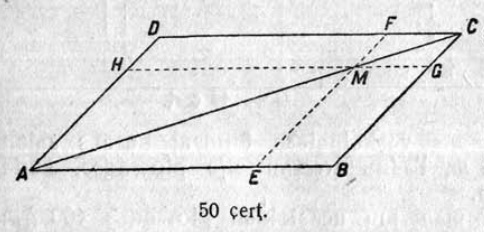
24. Сетӧм квадратын быд йыв ӧтлаалӧма кык водзвывса йыв костын куйлысь бок шӧркӧд (йывъяссӧ ӧти пӧрадокӧн лыддьӧмӧн). Ӧтлаалысь визьясыс вӧчӧны пытшкӧс квадрат. Докажитны (арталӧмӧн), мый сылӧн площадьыс сетӧм квадрат площадьысь ⅕ юкӧн ыджда.

25. Веськыд пельӧса куимпельӧсаӧ впишитӧма квадрат сідз, мый сылӧн ӧти бокыс куйлӧ гипотенуза вылас. Гипотенузалӧн бокса вундӧгъясыс m да n ыдждаӧсь. Определитны тайӧ квадратлысь площадьсӧ.

26. Сетӧм квадратса быд йывсянь водзвывса йылас нуӧдӧма 120° ыджда пытшкӧс дуга. Дугаяслысь вомӧнассянін чутъяссӧ мӧда-мӧдыскӧд ӧтлаалӧма, мый вӧсна артмис пытшкӧс квадрат. Корсьны квадратъяс площадьлысь отношенньӧсӧ.

27. Гипотенузавывса чутысь лэдзӧма кыкнан катетыс вылӧ перпендикуляръяс, мый вӧсна артмис веськыднёльпельӧса. Определитны сылысь площадьсӧ, катетъясыслӧн кӧ гипотенузабердса вундӧгъясыс m да n ыдждаӧсь.

28. 30 см подувтаса да 10 см судтаа куимпельӧсаӧ впишитӧма 63 см² площадя веськыднёльпельӧсаӧс. Определитны сылысь бокъяссӧ.

Куимпельӧса.

29. Быд квадратнӧй сантиметр вылӧ сынӧд личкӧ 1,03 кг вынӧн. Корсьны сынӧдлысь личкӧмсӧ куимпельӧсаа площадка вылӧ, кодлӧн подувтасыс 0,13 м да судтаыс 0,18 м ыдждаӧсь.

30. Определитны куимпельӧсалысь площадьсӧ, сылӧн кӧ подувтасыс да судтаыс соответственнӧя со мый ыдждаӧсь: 1) 32 см да 18 см; 2) 5 дм да 4 м; 3)

31. 1) ABC куимпельӧсаӧс пӧртны сыкӧд ӧтгырсяӧ сідз, медым BC бокыс эз вежсьы, а ABC пельӧссӧ вӧлі вежӧма сетӧм α пельӧсӧн.

2) ABC куимпельӧсаӧс пӧртны BC подувтаса кык ӧткузя бока ӧтгырся куимпельӧсаӧ.

32. 1) Сетӧм куимпельӧсаӧс юкны 3 ӧтгырся куимпельӧсаӧ ӧти йылысь петан веськыд визьясӧн.

2) Сетӧм параллелограммӧс юкны 4 ӧтгырся юкӧнӧ ӧти йылысь петан веськыд визьясӧн.

3) Сетӧм параллелограммӧс юкны 3 ӧтгырся юкӧнӧ ӧти йылысь петан веськыд визьясӧн.

33. Определитны куимпельӧсалысь площадьсӧ, кор сетӧма a да b бокъяссӧ да на костса пельӧссӧ, коді 1) 30°, 2) 45°, 3) 60° ыджда.

34. Куимпельӧсаын кӧ кык бокыс 3 см да 8 см, вермас-ӧ сылӧн площадьыс лоны 1) 10 см², 2) 15 см², 3) 12 см² ыджда?

35. 1) Веськыд пельӧса куимпельӧсалысь определитны площадьсӧ, кодлӧн гипотенузаыс 313 см, а ӧти катетыс 312 см.

2) Веськыд пельӧса куимпельӧсалӧн площадьыс 720 см² ыджда, катетъясыс относитчӧны кыдз 9 : 40. Определитны гипотенузасӧ.

3) Сетӧма a да b катетъяссӧ. Определитны на серти гипотенуза вылӧ нуӧдӧм судтасӧ.

36. Определитны кык ӧткузя бока веськыд пельӧса куимпельӧсалысь площадьсӧ c гипотенуза сертиыс.

37. Определитны кык ӧткузя бока куимпельӧсалысь площадьсӧ, сылӧн кӧ подувтасыс да боквывса бокыс 1) 56 см да 1 м, 2) b да c; 3) 20 см да 11 см.

38. Куимпельӧса бок вылын сетӧм чут пыр нуӧдны веськыд визь сідз, медым сійӧ куимпельӧсаыслысь площадьсӧ юкис шӧри.

39. 1) Определитны ӧткузя бокъяса куимпельӧсалысь площадьсӧ a бокыс серті.

2) Определитны ӧткузя бокъяса куимпельӧсалысь боксӧ Q площадьыс серти.

3) Определитны ӧткузя бока куимпельӧсалысь площадьсӧ h судта сертиыс.

40. 1) R радиуса кругӧ впишитӧм правильнӧй куимпельӧсалысь определитны площадьсӧ.

2) Определитны r радиуса круг гӧгӧр опишитӧм правильнӧй куимпельӧсалысь площадьсӧ.

41. Определитны веськыд пельӧса куимпельӧсалысь площадьсӧ, судтаыс кӧ сылӧн гипотенузасӧ юкӧ 32 см да 18 см кузя вундӧгъясӧ.

42. Определитны куимпельӧсалысь площадьсӧ, судтаыс кӧ сылӧн 36 см ыджда да боквывса бокъясыс 85 см да 60 см.

43. Определитны веськыд пельӧса куимпельӧсалысь катетъяссӧ, сылӧн кӧ гипотенузаыс 73 см, а площадьыс 1320 см² ыджда.

44. Кык ӧткузя бока куимпельӧсаын боквывса бокыс 10 см, площадьыс 48 см². Определитны подувтассӧ.

45. 1) Определитны ромблысь площадьсӧ, диагональясыс кодлӧн 72 см да 40 см кузяӧсь.

2) Определитны ромблысь судтасӧ, диагональясыс кӧ сылӧн 16 м да 12 м.

46. Определитны ромблысь боксӧ, диагональясыс кӧ относитчӧны кыдз m : n да площадьыс Q ыджда.

47. Куимпельӧсаын подувтас шӧрсьыс нуӧдӧма веськыдъясӧс боквывса бокъясыслы параллельнӧя. Докажитны, мый та ногӧн артмӧм параллелограмм ӧтгырся куимпельӧса джынкӧд.

48. Параллелограмм пытшкын босьтӧм кутшӧмкӧ чутӧс кӧ ӧтлаавны веськыдъясӧн став йывъясыскӧд, кык воча куйлысь куимпельӧсалӧн суммаыс ӧтгырся мӧд кык куимпельӧса суммаыскӧд. Докажитны тайӧс.

49. Сетӧм куимпельӧсаӧс пӧртны ӧтыджда (равновеликӧй) параллелограммӧ.

50. Сетӧм унапельӧсаӧс пӧртны ӧтыджда (равновеликӧй) унапельӧсаӧ жӧ, кодлӧн бокъяс лыдыс медым вӧлі ӧтиӧн этшаджык сетӧмсяысь.

51. Туй полотнолӧн пасьтаыс a = 6,75 м (51 чертёж); h — полотнолӧн насыпсянь джуджда, колӧ, медым h джудждаыс вӧлі полотно пасьтасьыс 2% ыджда; насыпыслӧн джудждаыс H = 1,5 м; откосъясыс пӧлыняӧсь горизонт визьлы 45° улын. Артавны туй вомӧна профильыслысь площадьсӧ.

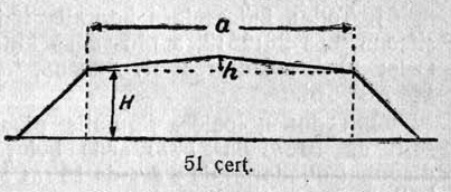
52. Определитны куимпельӧсалысь площадьсӧ, подувтасыс кӧ a ыджда да сы бердса пельӧсъясыс 30° да 45°.

53. ACB да ADB ӧтыджда веськыд пельӧса куимпельӧсаяс куйлӧны ӧтувъя AB гипотенузасяныс ӧтар бокын; та дырйи AD = BC = 12 см да AC = BD = 16 см. Определитны сетӧм куимпельӧсаясса ӧтувъя юкӧныслысь площадьсӧ.

54. Ӧткузя бокъяса куимпельӧсаын бокъяс вылас вӧчӧма квадратъясӧс да йывъяссӧ сылысь ӧтлаалӧма. Определитны артмӧм квайтпельӧсалысь площадьсӧ, куимпельӧсаыслӧн бокыс кӧ a ыджда.^Вуджӧдӧмын бок кузьтаыс абу сетӧма./^

55. a бока сетӧм квадратӧс пельӧсъясӧдыс вундалӧма сідз, мый артмӧма правильнӧй 8‐пельӧса. Определитны тайӧ 8‐пельӧсалысь площадьсӧ.

56. Веськыд пельӧса куимпельӧсаын катетъяслӧн отношенньӧыс 1,05; описаннӧй да вписаннӧй кругъяслӧн радиусъяскостса разносьтыс 17 дм. Определитны куимпельӧсаыслысь площадьсӧ.

57. 150 см да 200 см диагональяса ромбын тшӧтшыд пельӧс йывсяньыс нуӧдӧма судтаяс да налысь помъяссӧ ӧтлаалӧма. Определитны та ногӧн артмӧм куимпельӧсалысь площадьсӧ.

58. AB да CD — кык параллельнӧй вундӧг; вундӧгъяслысь помъяссӧ ӧтлаалӧма крестӧн AD да BC веськыдъясӧн, налӧн вомӧнассяніныс — M чут. AB = 8 см; CD = 12 см; на костса расстоянньӧыс 10 см ыджда. Определитны ∆ABM да ∆MCD площадьяслысь сумма.

Геронлӧн формула.

59. Куим бок серти определитны куимпельӧсалысь площадьсӧ:

1) 13; 14; 15. 2) 29; 25; 6. 3) 5; 6; 9. 4) 3; 5; 7.

5) 6; 5; 2,2. 6) 5; 8⅔; 12⅓. 7) 5; 4;

60. 1) Куимпельӧсалӧн бокъясыс: 25 дм; 29 дм; 36 дм. Определитны сылысь ичӧтджык судтасӧ.

2) Куимпельӧсалӧн бокъясыс: 15, 112 да 113. Определитны сылысь ыджыд судтасӧ.

61. Определитны куимпельӧсалысь бокъяссӧ: 1) найӧ кӧ относитчӧны кыдз 26 : 25 : 3 да куимпельӧсаыслӧн площадьыс 9 м²; 2) бокъясыс кӧ относитчӧны кыдз 9 : 10 : 17 да площадьыс 144 см².

62. Определитны нёльпельӧсалысь площадьсӧ, кор сылӧн диагональыс 17 см, диагональсяньыс ӧтарла бокас куйлысь бокъясыс 10 см да 21 см, а мӧдарла бокас — 8 см да 15 см.

63. Кык вомӧнассян кытшвизьлӧн радиусъясыс 17 см да 39 см да шӧр чутъяскостса расстоянньӧыс 44 см. Определитны ӧтувъя хордаыслысь кузьтасӧ.

64. Определитны параллелограммлысь площадьсӧ, сылӧн кӧ ӧти бокыс 51 см ыджда, а диагональясыс — 40 см да 74 см.

65. Определитны куимпельӧсалысь площадьсӧ, сылӧн кӧ кык бокыс 27 см да 29 см да коймӧд бокса медианаыс 26 см ыджда.

66. Куимпельӧсалысь сетӧма кык боксӧ да площадьсӧ; тайӧяс серти определитны коймӧд боксӧ: 1) a = 17, b = 28, S = 210; 2) a = 7, b = 11, S =

67. ABC куимпельӧсаын сетӧма 3 боксӧ. AB = 26, BC = 30 да AC = 28. B йывсяньыс нуӧдӧма судта да биссектриса. Определитны судтаа-биссектрисаа костӧ йӧртӧм юкӧнлысь площадьсӧ.

68. Куимпельӧсалӧн бокъясыс: 13 см, 14 см, 15 см. Нуӧдӧма кытшвизь сідз, мый сылӧн шӧр чутыс шӧр бок вылас да мӧд кык бокас сійӧ касайтчӧ. Определитны сылысь радиуссӧ.

69. Сетӧм куимпельӧсалысь йывъяссӧ ӧтлаалӧма вписаннӧй кытшвизь шӧр чуткӧд. Нуӧдӧм визьясӧн куимпельӧсалӧн площадьыс юксис 3 юкӧнӧ: 28 м², 60 м² да 80 м². Определитны сетӧм куимпельӧсалысь бокъяссӧ.

70. ABCD нёльпельӧсаын сетӧма: AB = 26 см, BC = 30 см, CD = 17 см, AD = 25 см да AC диагональ = 28 см. Определитны нёльпельӧсалысь площадьсӧ да BD диагональсӧ.

Трапециялӧн площадь.

71. 1) Трапециялӧн подувтасъясыс 35 см да 29 см ыдждаӧсь, а площадьыс 256 см². Определитны трапециялысь судтасӧ.

2) Трапецияын судтаыс 8 см, а площадьыс 2 дм². Определитны шӧр визьыслысь кузьтасӧ.

3) Трапециялӧн площадьыс = 144 см²; подувтасъясыс относитчӧны кыдз 4 : 5; судтаыс = 16 см. Определитны подувтасъяссӧ.

72. Определитны стрелкӧвӧй окоплысь вомӧна сеченньӧыслысь площадьсӧ (52 чертёж). Размеръяссӧ сетӧма метръясын.

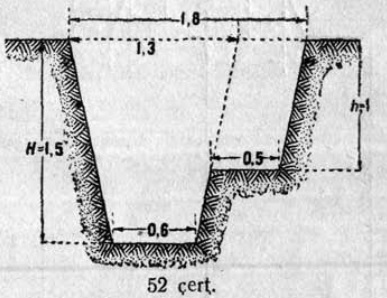
73. Артавны юлысь вомӧна сеченньӧ площадьсӧ. Плансӧ сетӧма 53 чертёж вылын, джуджда размеръяссӧ табличаын:

Берегсянь расстоянньӧыс метръясӧн.	0	1	2	3	4	5	6	7	8	9	10
Джудждаыс метръясӧн	0	0,65	0,9	1,5	1,85	2,4	2,35	1,75	1,25	0,6	0

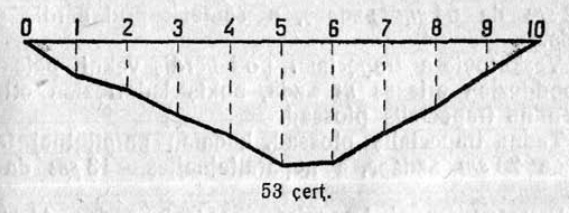
74. 54 чертёж вылын рабочӧй клубса столӧвӧйлӧн планыс; размеръяссӧ сетӧма метръясӧн. Определитны столӧвӧйлысь площадьсӧ.

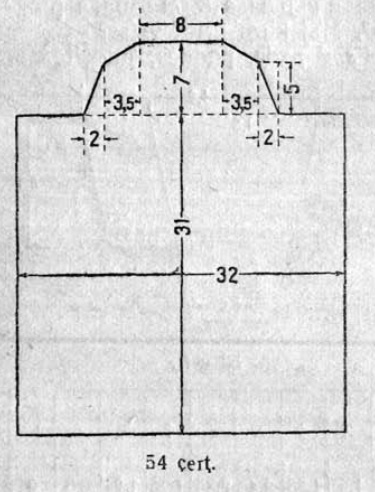
75. Военнӧй маскировка вылӧ костюм вуригӧн пӧльзуйтчӧны 55ʼ чертёж вылын петкӧдлӧм выкройкаӧн; размеръяссӧ сетӧма сантиметръясын. Артавны выкройкаыслысь площадьсӧ.

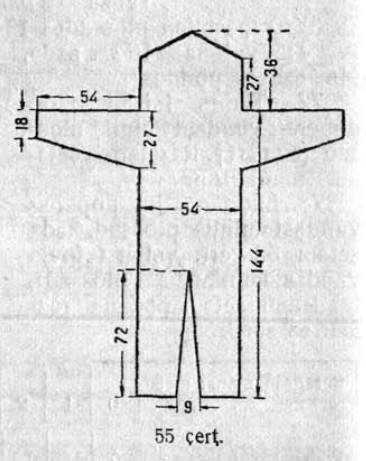
76. 1) ABCD трапециялысь площадьсӧ юкӧма шӧри EF веськыд визьӧн, кодӧс нуӧдӧма AB боквывса бокыслы параллельнӧя. Определитны AF вундӧг, AD кӧ = 28 см да BC = 12 см.

2) Трапециялӧн площадьыс диагональнас юксьӧ 3 : 7 отношенньӧын. Кутшӧм отношенньӧын сійӧ юксьӧ шӧр визьнас ичӧтик подувсяньыс босьтӧмӧн?

77. Кык ӧткузя бока трапецияын подувтасъясыс 51 см да 69 см, а боквывса бокыс 41 см. Определитны площадьсӧ.

78. Определитны кык ӧткузя бока трапециялысь площадьсӧ, кӧн подувтасъясыс 42 см да 54 см да ыджыд подувтасбердса пельӧсыс 45° ыджда.

79. Веськыд пельӧса трапецияын подувтасбердса ёсь пельӧсыс 30°, подувтасъясыслӧн суммаыс m ыджда да боквывса бокъяслӧн суммаыс n ыджда. Определитны трапециялысь площадьсӧ.

80. Определитны трапециялысь площадьсӧ, кодлӧн параллельнӧй бокъясыс 60 см да 20 см, а мукӧд кык бокыс 13 см да 37 см.

81. Кык ӧткузя бока трапецияын ыджыдджык подувтасыс 44 м, дорса бокыс 17 м, диагональыс 39 м. Определитны трапециялысь площадьсӧ.

82. 1) Определитны кык ӧткузя бока трапециялысь площадьсӧ, кодлӧн подувтасъясыс 12 см да 20 см, а диагональясыс мӧда-мӧдыслы перпендикулярнӧйӧсь.

2) Определитны кык ӧткузя бока трапециялысь площадьсӧ, кодлӧн диагональясыс мӧда‐мӧдыскӧд перпендикулярнӧйӧсь, а судтаыс h ыджда.

83. Определитны кык ӧткузя бока трапециялысь площадьсӧ, сылӧн кӧ диагональыс c ыджда да ыджыдджык подувтасыскӧд вӧчӧ 45°-а пельӧс.

84. Определитны кык ӧткузя бока трапециялысь площадьсӧ, кодлӧн подувтасъясыс 10 см да 26 см ыдждаӧсь, а диагональясыс боквывса бокъясыслы перпендикулярнӧйӧсь.

85. Трапецияын подувтасъясыс 142 см да 89 см, диагональясыс 120 см да 153 см. Определитны площадьсӧ.

86. R радиуса кругын шӧр чутсянь ӧтар боктіыс нуӧдӧма кык параллельнӧй хордаяс, кодъяс стягивайтӧны 60°-а да 120°‐а дугаяс. Налысь помъяссӧ ӧтлаалӧма. Определитны артмӧм трапециялысь площадьсӧ.

87. Круг гӧгӧр опишитӧм кык ӧткузя бока трапецияын боквывса бокыс a ыджда да подувтасбердса ёсь пельӧсыс 30° ыджда. Определитны трапецияыслысь площадьсӧ.

88. 1) Куимпельӧсалӧн подувтасыс = 75 см да боквывса бокъясыс 65 см да 70 см. Йывсяньыс лыддьӧмӧн судтасӧ юкӧма 2 : 3 отношенньӧын; юкан чут пырыс нуӧдӧма подувтасыслы параллельнӧя веськыдӧс. Определитны та дырйи артмӧм трапециялысь площадьсӧ.

2) Трапецияын диагональясыс 20 м да 15 м; судтаыс 12 м. Определитны трапециялысь площадьсӧ.

89. Кык ӧткузя бока трапециялӧн подувтасъясыс да боквывса бокыс относитчӧны кыдз 10 : 4 : 5. Сылӧн площадьыс = 112 см². Корсьны трапециялысь периметрсӧ.

Унапельӧсалӧн площадь.

90. 56 чертёж вылын сетӧма му участоклысь плансӧ 1 : 10000 масштабӧн. Мурталӧма сылысь диагональяссӧ d₁ да d₂ да судтаяссӧ: h₁, h₂ да h₃. Сетӧма: d₁ = 44 мм; d₂ = 50 мм; h₁ = 7 мм; h₂ = 20,4 мм да h₃ = 21,6 мм. Артавны му участоклысь площадьсӧ гектаръясын.

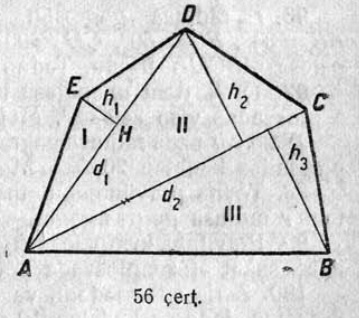
91. Артавны му участоклысь площадьсӧ; плансӧ сетӧма 57 чертёж вылын; размеръясыс — метръясӧн.

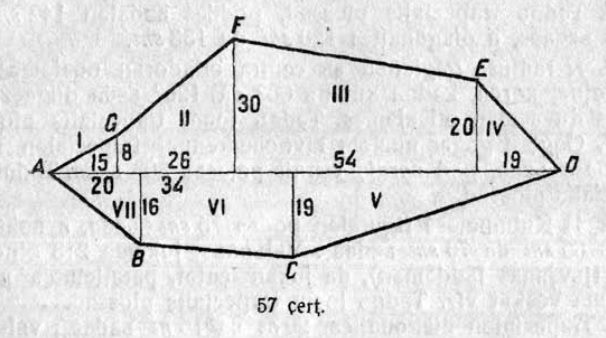
92. Нёльпельӧсаын диагональясыс k да l ыдждаӧсь да: 1) мӧда-мӧдыслы перпендикулярнӧйӧсь, 2) вӧчӧны 30°-а пельӧс. Определитны нёльпельӧсалысь площадьсӧ.

93. Веськыднёльпельӧсаын бокъяс вылас ортсыласяньыс вӧчалӧма ӧткузя бокъяса куимпельӧсаясӧс да налысь прӧст йывъяссӧ йитӧма. Артавны артмӧм нёльпельӧсалысь^Вуджӧдӧмын ӧшыбка, гижӧма "веськыднёльпельӧса". — А.В."/^ площадьсӧ, кор сылӧн бокъясыс a да b ыдждаӧсь.

94. AE вундӧг вылын босьтӧма C чут сідз, мый AC = a да CE = b; AC да CE вундӧгъяс вылӧ ӧтарла бокъясас вӧчӧма ABC да CDE ӧткузя бокъяса куимпельӧсаясӧс да B да D йывъяссӧ ӧтлаалӧма. Определитны ABDE нёльпельӧсалысь площадьсӧ.

95. ABCD нёльпельӧсаын M чут AD боклӧн шӧрыс. Сетӧма: MB ⟂ AB; MC ⟂ CD; AD = 50 см; AB = 15 см да CD = 7 см. Определитны ABCD‐лысь площадьсӧ.

96. r радиуса кытшвизь вылын последовательнӧя босьтӧма дугаясӧс: AB = 30°; BC = 60°; CD = 90° да DE = 120° да вӧчӧма ABCDE 5-пельӧсаӧс. Определитны сылысь площадьсӧ.

97. 1) Описаннӧй унапельӧсалӧн периметрыс = 60 см, а площадьыс 240 см². Определитны кругыслысь радиуссӧ.

2) 25 см кузя радиуса кытшвизь гӧгӧр опишитӧма 20 дм² площадя унапельӧсаӧс. Определитны сылысь периметрсӧ.

98. Определитны r радиуса кытшвизь гӧгӧр опишитӧм правильнӧй куимпельӧсалысь площадьсӧ.

99. Правильнӧй 6-пельӧсалӧн бокыс 84 см ыджда; артавны сыкӧд ӧтгырся правильнӧй куимпельӧсалысь боксӧ.

100. 7,48 м кузя да 3,25 м пасьта джодж кӧсйӧны вевттьыны 12 см бока правильнӧй 6-пельӧса формаа паркетӧн. Кымын паркетнӧй плитка ковмас?

101. 5,6 м кузя да 4,5 м пасьта комнаталӧн ӧти помас эм правильнӧй 6-пельӧса джын^Вуджӧдӧмын вунӧдӧма "джын". — А.В./^ формаа содтӧд площадь, кодлӧн бокыс 1,6 м ыджда. Определитны комнаталысь площадьсӧ.

102. 1) Сетӧм R радиус серти определитны правильнӧй вписаннӧй квайтпельӧсалысь площадьсӧ.

2) Сетӧм r радиус серти определитны правильнӧй описаннӧй квайтпельӧсалысь площадьсӧ.

3) Сетӧм S площадь серти определитны правильнӧй квайтпельӧсалысь боксӧ^Вуджӧдӧмын гижӧма "площадьсӧ". — А.В./^.

103. Сетӧм R радиус серти определитны правильнӧй вписаннӧй 8-пельӧсалысь да 12-пельӧсалысь площадьяссӧ.

104. Железобетоннӧй сваялӧн сеченньӧыс правильнӧй кӧкъямыспельӧса формаа. Воча йывъяскостса медыджыд расстоянньӧыс 224 мм. Определитны сеченньӧыслысь площадьсӧ.

105. 8-грана кӧртлӧн медічӧт кызтаыс (воча гранъяскостса расстоянньӧыс) = 36 мм. Артавны вомӧна сеченньӧыслысь площадьсӧ.

106. 1) Правильнӧй вписаннӧй 12-пельӧсалысь сетӧм Q площадь серти определитны сійӧ жӧ кытшвизьӧ впишитӧм правильнӧй 6-пельӧсалысь площадьсӧ.

2) Правильнӧй вписаннӧй 8-пельӧсалысь сетӧм Q площадь серти определитны сійӧ жӧ кытшвизьӧ впишитӧм квадратлысь площадьсӧ.

107. 1) R радиуса кытшвизьӧс юкӧма 6 ӧтыджда юкӧнӧ да юкан чутъяссӧ быд ӧти вомӧн ӧтлаалӧма. Определитны артмӧм квайтпельӧса звездалысь площадьсӧ.

2) R радиуса кытшвизьӧс юкӧма 8 ӧтыджда юкӧнӧ да юкан чутъяссӧ ӧтиӧн-ӧтиӧн ордйӧмӧн ӧтлаалӧма. Определитны артмӧм 8-пельӧса звездалысь площадьсӧ.

Куимпельӧсаяслысь да унапельӧсаяслысь площадьяс ӧтластитӧм.

108. 1) Докажитны, мый быд веськыд, коді мунӧ параллелограммын симметрия шӧр чутыс пыр, юкӧ сійӧс 2 ӧтыджда (равновеликӧй) юкӧнӧ.

2) Сетӧм чут пыр нуӧдны сэтшӧм веськыдӧс, коді медым сетӧм параллелограммлысь площадьсӧ юкис шӧри.

109. Сетӧм параллелограммӧс йывсьыс петысь веськыд визьясӧн юкны n ӧтгырся юкӧнӧ, 1) n кӧ = 6; 2) n = 5.

110. Нёльпельӧсаын ӧти диагональ шӧрсьыс нуӧдӧма воча йывъясас веськыд визьясӧс. Докажитны, мый тайӧ веськыдъяс нёльпельӧсасӧ юкӧны 2 ӧтгырся юкӧнӧ.

111. Докажитны, мый кутшӧмкӧ нёльпельӧсаын кӧ диагональыс юкӧ мӧд диагональсӧ шӧри, сійӧ сідзжӧ шӧри юкӧ нёльпельӧсаыслысь площадьсӧ.

112. 1) Докажитны, мый трапецияын параллельнӧй бокъяс шӧр пырыс мунысь веськыд визь юкӧ сійӧс 2 ӧтгырся юкӧнӧ.

2) Трапецияын подувтасъясыслысь шӧръяссӧ ӧтлаалысь визь вылын босьтӧма чут да сійӧс ӧтлаалӧма трапецияса став йылыскӧд. Докажитны, мый боквывса бокъясбердса куимпельӧсаясыс ӧтгырсяӧсь.

113. 1) Трапециялӧн диагональясыс юкӧны сійӧс 4 куимпельӧса вылӧ. Докажитны, мый боквывса бокъясбердса куимпельӧсаясыс ӧтгырсяӧсь.

2) Трапецияын кӧ ӧти AB боквывса боклысь M шӧрсӧ ӧтлаавны мӧд боквывса CD бок помъясыскӧд, артмӧм CMD куимпельӧсалӧн площадьыс трапеция площадь джын ыджда. Докажитны.

114. Трапециялӧн диагональыс юкӧ сылысь площадьсӧ 3 : 7 отношенньӧын. Кутшӧм отношенньӧын юксяс трапециялӧн площадьыс, вылыс подувтас помсяньыс кӧ боквывса бокыслы параллельнӧя нуӧдны веськыд визь?

115. 1) Вӧчны a да b бокъяса кык сетӧм квадрат суммалы ӧтыджда (равновеликӧй) квадратӧс (a = 5 см, b = 12 см).

2) Вӧчны квадрат, кодлӧн площадьыс медым вӧлі 3 пӧв ыджыдджык a бока сетӧм квадрат площадьысь.

116. Веськыд пельӧса куимпельӧса бокъяс вылӧ вӧчӧма квадратъясӧс да налысь свободнӧй йывъяссӧ ӧтлаалӧма. Определитны артмӧм квайтпельӧсалысь площадьсӧ, сетӧм куимпельӧсалӧн кӧ катетъясыс a да b ыдждаӧсь.

117. Кык куимпельӧсалӧн эм ӧти ӧтыджда пельӧсӧн, коді первой куимпельӧсаын 12 дм да 28 дм кузя бокъяс костын, а мӧдыс 21 дм да 24 дм кузя бокъяс костын. Кыдз относитчӧны тайӧ куимпельӧсаяслӧн P да Q площадьясыс?

118. ABC куимпельӧсалысь BA боксӧ нюжӧдӧма AD = 0,2BA кузьта вылӧ да BC CE = ⅔BC кузьта вылӧ; D да E чутъяссӧ ӧтлаалӧма. Корсьны ABC да DBE площадьяслысь отношенньӧсӧ.

119. Куимпельӧсаса биссектрисалысь свойствосӧ петкӧдны площадьясӧс ӧтластитӧмысь.

120. Кымын пӧв ыдждас куимпельӧсалӧн площадьыс, сылысь кӧ быд бок ыдждӧдны 4 пӧв? 5 пӧв?

121. Куимпельӧсалӧн бокыс 5 дм ыджда. Мый ыджда сходственнӧй бокыс сылы подобнӧй куимпельӧсалӧн, кодлӧн площадьыс 2 пӧв ыджыдджык?

122. Кутшӧм юкӧн площадьлысь (йывсянь лыддьӧмӧн) вундӧ куимпельӧсалӧн шӧр визьыс?

123. Куимпельӧсаын судтаыс h ыджда. Кутшӧм расстоянньӧ сайын йывсяньыс мунӧ подувтаслы параллель, коді куимпельӧсаыслысь площадьсӧ юкӧ шӧри?

124. 1) Куимпельӧсалысь боквывса боксӧ юкӧма 2 : 3 : 4 отношенньӧын (йывсяньыс подувланьыс) да юкан чутъяссьыс нуӧдӧма подувтасыслы параллельнӧй веськыдъясӧс. Кутшӧм отношенньӧын юксис куимпельӧсалӧн площадьыс?

2) ABC куимпельӧсалысь AB боксӧ m : n отношенньӧын юкысь E чут пыр нуӧдӧма BC‐лы параллель. Кутшӧм отношенньӧ лои вундӧм куимпельӧсаса да артмӧм трапецияса площадьяс костын?

125. Куимпельӧсаын подувтаслы параллельнӧй веськыд визь боквывса боксӧ юкӧ (йывсяньыс лыддьӧмӧн) 5 : 3 отношенньӧын, а площадьсӧ сэтшӧм юкӧнъясӧ, кодъяслӧн разносьтыс 56 см² ыджда. Определитны куимпельӧсалысь площадьсӧ ставнас.

126. Подувтаслы параллельнӧй веськыд визьясӧн куимпельӧсалӧн площадьыс (йывсяньыс подувтасланьыс) юксис 9 : 55 : 161 отношенньӧын. Кутшӧм отношенньӧын юксисны боквывса бокъясыс?

127. Ӧти нима описаннӧй фигуралысь кутшӧм площадь пай составляйтӧны татшӧм вписаннӧй фигураяслӧн площадьяс: 1) правильнӧй куимпельӧса; 2) квадрат; 3) правильнӧй квайтпельӧса (решитны площадьяссӧ артавтӧг)?

128. Куим подобнӧй унапельӧсаяслӧн площадьяс суммаыс 232 дм² ыджда, а периметръясыс относитчӧны кыдз 2 : 3 : 4. Определитны быд унапельӧсалысь площадьсӧ.

129. Веськыд пельӧса куимпельӧсаын катетъяс вылӧ вӧчӧма подобнӧй фигураяс, та дырйи куимпельӧсалӧн бокъясыс лоӧны тайӧ фигураясса сходственнӧй бокъясӧн. Докажитны, мый гипотенуза вылӧ вӧчӧм фигуралӧн площадьыс равняйтчӧ катетъяс вылӧ вӧчӧм фигураясса площадьяс суммалы.

130. 1) Вӧчны квадрат, медым сійӧ вӧлі кык сетӧм квадратъяс разносьткӧд ӧтыджда.

2) Вӧчны квадрат, медым сійӧ вӧлі n сетӧм квадратъяс суммакӧд ӧтыджда.

131. Вӧчны куимпельӧсаӧс, медым сійӧ вӧлі сетӧм унапельӧсакӧд ӧтыджда.

132. Сетӧма кык квадрат боклысь^Вуджӧдӧмын вунӧдӧма "бок". — А.В./^ отношенньӧ да на пиысь ӧти квадратсӧ; вӧчны мӧд квадратсӧ.

133. Параллелограммын ӧти направленньӧӧд ӧтлаалӧма быд боклысь шӧрсӧ локтан бок помыскӧд, мый вӧсна артмӧма пытшкӧс параллелограмм. Докажитны, мый сылӧн площадьыс сетӧм параллелограмм площадь ⅕ юкӧныс ыджда.

134. Кыдзи мӧда-мӧд костас относитчӧны подувтасъясыс сэтшӧм трапециялӧн, коді ӧтыджда (равновеликӧй) ас дополнительнӧй куимпельӧсаыслы?

135. Веськыд пельӧса куимпельӧсалысь площадьсӧ гипотенузалы перпендикулярнӧй веськыд визьӧн юкӧма шӧри. Ыджыд катетыс 20 м ыджда. Корсьны тайӧ веськыд визьсянь ичӧт ёсь пельӧс йылӧдз расстоянньӧсӧ.

136. Веськыд пельӧса куимпельӧсаын катетъясыс относитчӧны кыдз 3 : 4, а судтаыс куимпельӧсаыслысь площадьсӧ юкӧ юкӧнъясӧ, кодъяслӧн разносьтыс 84 дм² ыджда. Определитны куимпельӧсалысь площадьсӧ ставнас.

137. 1) ABC куимпельӧсалӧн 3 медианаыс вомӧнассьӧны M чутын. Докажитны, мый AMB куимпельӧса — ABC куимпельӧсалӧн коймӧд юкӧныс.

2) Докажитны, мый куимпельӧсаын куим медиана сылысь площадьсӧ юкӧны 6 ӧтыджда юкӧнӧ.

138. Ортсыса A чутысь круг бердӧ нуӧдӧма AB касательнӧйӧс да ACD секущӧй. Определитны CBD куимпельӧсалысь площадьсӧ, кор AC : AB = 2 : 3 да ABC площадь = 20 дм².

139. AB да CD — кык хорда, кодъяс оз вомӧнассьыны; ‿AB = 120°; ‿CD = 90°; M лоӧ AD да BC хордаяслӧн вомӧнассянін чут. Определитны AMB-лысь да CMD-лысь площадьяссӧ, суммаыс кӧ налӧн 100 см² ыджда.

140. AB — диаметр; BC да AC хордаяс, та дырйи ‿BC = 60°. D лоӧ нюжӧдӧм диаметрлӧн да CD касательнӧйлӧн вомӧнассянін чут. Корсьны DCB да DCA площадьяслысь отношенньӧсӧ.

141. Квадратлысь быд бок бергӧдӧма, кыдз петкӧдлӧма 58 чертёж вылын, 30° вылӧ квадрат пытшкӧсланьыс. Определитны сетӧм квадрат да [...]

15 §. Кытшвизьлӧн да дугалӧн кузьта. Круглӧн да сійӧ юкӧнъясыслӧн площадь.

Кытшвизьлӧн да дугалӧн кузьта

1. Артавны кытшвизьлысь кузьтасӧ, радиусыс кӧ сылӧн: 1) 10 м; 2) 15 м; 3) 35 м.

2. Артавны радиус, кытшвизьыслӧн кӧ кузьтаыс: 1) 1 м; 2) 25 см; 3) 4,75 дм.

3. Зубчатӧй кӧлесаын, кодлӧн диаметрыс 0,66 м ыджда, кык пинь шӧръяскостса расстоянньӧыс 34,5 мм ыджда (дуга кузяыс лыддьӧмӧн). Кымын пинь кӧлесаын?

4. 1,4 м кузя диаметра шкив минутын бергӧдчӧ 80-ысь. Определитны тайӧ шкивлысь кытшвизьса ӧдсӧ.

5. Сетӧм R радиус серти определитны кузьтасӧ дугалысь, кӧн: 1) 45°; 2) 24°30′; 3) 5°14′15″.

6. Определитны дугалысь радиуссӧ, дуга кӧ l кузя да сыын: 1) 135°; 2) 10°40′.

7. Шкивлӧн кытшвизьыс (59ʼ чертёж) 540 мм кузя; шкивас 200 мм дуга вылын касайтчӧ тасма. Определитны шкивӧс тасмаӧн кватитан α пельӧссӧ.

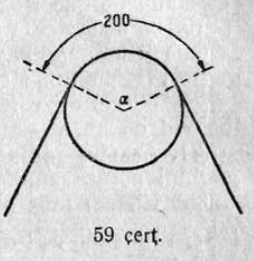
8. Кӧрт туй закругленньӧлӧн радиусыс 1200 м ыджда; дугаыслӧн кузьтаыс 450 м. Кымын градус дугаас?

9. 1) 2 см радиуса кытшвизьысь вӧчисны 5 см радиуса дуга. Корсьны артмӧм центральнӧй пельӧссӧ.

2) 4 см радиуса дуга, коді мурталӧ 120°-а центральнӧй пельӧсӧс, равняйтчӧ кутшӧмкӧ кытшвизь кузьталы. Корсьны тайӧ кытшвизьлысь радиуссӧ.

3) 6 см радиуса кытшвизьӧс паськӧдісны 300° ыджда центральнӧй пельӧсӧс мурталысь дугаӧ. Корсьны дугаыслысь радиуссӧ.

10. Определитны дугалысь градус лыдсӧ, кор сылысь сетӧма R радиуссӧ да l кузьтасӧ: 1) R = 10, l = 45; 2) R = 15, l = 6.

11. Кымын градус да минут сэтшӧм дугаын, кодлӧн кузьтаыс радиус ыджда (1/π = 0,31831)?

12. Сетӧм a хорда серти определитны сылысь дугасӧ, сыын кӧ: 1) 60°; 2) 90°; 3) 120°.

13. Сетӧм l кузя дуга серти определитны сылысь хордасӧ, дугаын кӧ: 1) 60°; 2) 90°; 3) 120°.

14. Определитны радиуссӧ кытшвизьлысь, кор сійӧ диаметрсьыс 107 см-ӧн кузьджык.

15. 1) Ёна-ӧ ыдждас кытшвизьлӧн кузьтаыс, радиуссӧ кӧ ыдждӧдны m вылӧ?

2) Шуам, мый быттьӧ му шарӧс экватор кузя асыкалӧма да сідз жӧ асыкалӧма ыджыдджык круг кузяыс футбол мачӧс. Водзӧ шуам, мый быттьӧ быд тайӧ асыклӧн кытшвизьыс кузяммис 1 м вылӧ. Сэк асыкъяс телӧяссьыс, кодъясӧс найӧ жмитісны, янсалӧны да на костын кольӧ кутшӧмкӧ кост. Кутшӧм случайын тайӧ костыс лоӧ ыджыдджык: му шарлӧн али футбол мачлӧн?

16. 1) 6 мм кызта стенкаа кӧрт трубалӧн ортсыса кытшвизьыс 22 см кузя. Корсьны пытшкӧс кытшвизьыслысь кузьтасӧ.

2) Кык концентрическӧй кытшвизь пиысь ӧтиыс 167 см кузя, а мӧдыс 117 см кузя. Определитны кольчалысь пасьтасӧ.

17. Определитны кытшвизьлысь кузьтасӧ, сійӧ кӧ правильнӧй вписаннӧй 6-пельӧсаса периметрысь 7 см-ӧн ыджыдджык.

18. Сегмент дугалӧн кузьтаыс l да сыын 120°. Определитны тайӧ сегментӧ впишитӧм кытшвизьлысь кузьтасӧ.

19. 120°-а ABC дуга помъяссянь нуӧдӧма мӧда-мӧдыскӧд D чутын вомӧнассьытӧдз касательнӧйясӧс да артмӧм ACBD фигураӧ впишитӧма кытшвизь. Докажитны, мый сійӧ ABC дуга ыджда.

20. 60‐ӧд чертёж вылын сетӧма парӧвӧй машинаса коленчатӧй трубалысь видсӧ, размеръясыс сантиметръясӧн. Корсьны сылысь кузьтасӧ.

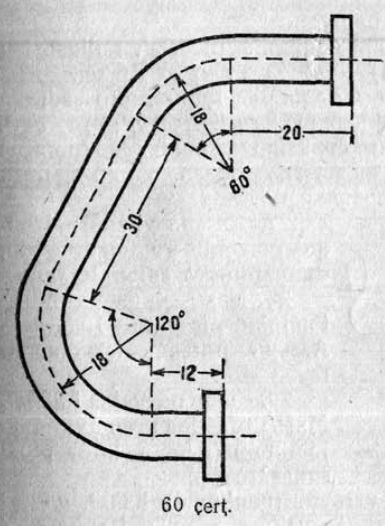
21. Корсьны сэтшӧм кытшвизьлысь радиус, кодлӧн кузьтаыс да кругыслӧн площадьыс мыччӧдсьӧ ӧти сійӧ жӧ лыдӧн.

22. Определитны относительнӧй погрешносьт, кор кытшвизь джынлысь ½C кузьтасӧ вежас a₃ + a₄ (кытшвизьӧс матыстӧмӧн веськӧдӧм вылӧ).

23. Кытшвизяс матыстӧмӧн веськӧдӧмъяс пиысь ӧти сэтшӧм, мый кытшвизьлысь кузьтасӧ вежӧны веськыд пельӧса куимпельӧсаса периметрӧн, кодлӧн ӧти катетыс диаметр 6⁄5 юкӧн ыджда, а мӧдыс — диаметр 3⁄5 юкӧн ыджда. Определитны абсолютнӧй погрешносьтсӧ.

Круглӧн площадь.

24. Определитны круглысь площадьсӧ, кор сылӧн радиусыс: 1) 10 м; 2) 4 дм; 3) 2,6^Вуджӧдӧмын вочакыв гижӧма ӧшыбкаӧн, арталӧма 2,5 ыджда радиуслы. — А.В./^ см.

25. Определитны круглысь радиуссӧ, площадьыс кӧ сылӧн: 1) 2 см²; 2) 50 м²; 3) 17 дм².

26. 1914 вося образеча ручнӧй граната взрыв дырйиыс сетӧ осколочнӧй пораженньӧ 45 м сайӧдз кымын взрывитчан местасяньыс. Определитны тайӧ гранаталысь поражайтан площадьсӧ.

27. Корсьны воздушнӧй насос поршеньлысь площадьсӧ, кодлӧн диаметрыс 10 см ыджда.

28. Насос поршеньлӧн площадьыс 12,56 см² ыджда. Корсьны поршеньлысь диаметрсӧ.

29. Пулӧн кытшвизьыс 1,884 м. Ыджыд-ӧ сылӧн вомӧна сеченньӧ площадьыс?

30. Кутшӧм груз лэптӧ 18 см кытшвизя пыш канат, позяна нагрузка кӧ 100 кг/см² ыджда?

31. 1) Определитны круглысь площадьсӧ, кытшвизьлӧн кӧ кузьтаыс 8 см.

2) Определитны кытшвизьлысь кузьтасӧ, кругыслӧн кӧ площадьыс 18 см² ыджда.

32. 1) ІІІ трубалӧн пропускнӧй способносьтыс (61ʼ чертёж) сэтшӧм жӧ, кутшӧм І да ІІ трубаяслӧн ӧттшӧтш босьтӧмӧн. Определитны построенньӧӧн чертёж вылын сетӧм размеръяс серти x-лысь величинасӧ.

2) 6 см да 8 см диаметра трубаясӧс колӧ вежны ӧти трубаӧн, кодлӧн пропускнӧй способносьтыс медым вӧлі кык воддзаыс ыджда. Тӧдны тайӧ трубалысь диаметрсӧ.

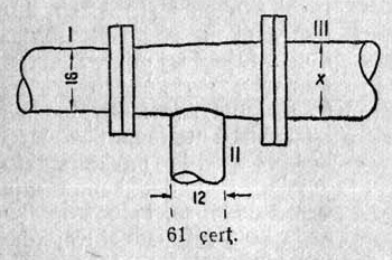
33. Определитны круглысь площадьсӧ, вписаннӧй квадратлӧн кӧ площадьыс F ыджда.

34. Артавны круглысь площадьсӧ, сійӧ кӧ описаннӧй квадрат площадьысь 4,3 м²-ӧн ичӧтджык.

35. Корсьны вписаннӧй да описаннӧй кругъяс площадьяс костысь отношенньӧсӧ: 1) правильнӧй куимпельӧсалы; 2) квадратлы; 3) правильнӧй квайтпельӧсалы.

Кольчалӧн площадь.

36. Вертикальнӧй цилиндрическӧй пӧртлӧн, кодлӧн диаметрыс 78 см да сьӧктаыс 652 кг, пыдӧсас эм розь, кодлӧн ортсыса диаметрыс 36 см ыджда. Пӧртыс пыдӧсса став площадьнас куйлӧ фундамент вылын. Определитны личкӧм, кодӧс вӧчӧ быд 1 см² фундамент веркӧс вылӧ пӧртлӧн сьӧктаыс.

37. Концентрическӧй кык кытшвизьысь артмӧм кольчаын ыджыдджык кытшвизьыслӧн хордаыс, коді касайтчӧ ичӧтджыкас, a ыджда. Определитны кольчалысь площадьсӧ.

38. Кругӧ касайтчӧны сыкӧд ӧтыджда 6 круг, кодъяс сідз жӧ касайтчӧны мӧда-мӧдыскӧд. Сизим ӧтыджда кругъяс соединенньӧсӧ кватитӧма сэтшӧм кольчаӧн, коді ыджданас найӧ суммалы равнӧй. Докажитны, мый кольчалӧн пасьтаыс кругъяс радиус ыджда.

Сектор да сегмент.

39. Определитны секторлысь площадьсӧ, радиусыс кӧ r ыджда да дугаын: 1) 67°30′; 2) 15°45′.

40. Определитны секторлысь радиуссӧ, сылӧн кӧ площадьыс q ыджда да центральнӧй пельӧсыс 1) 72°; 2) 36′.

41. Секторлӧн радиусыс r ыджда, а площадьыс q ыджда. Определитны центральнӧй пельӧслысь (либӧ дугалысь) величинасӧ.

42. Определитны сегментлысь площадьсӧ, радиусыс кӧ R ыджда да дугаас: 1) 90°; 2) 60°; 3) 45°; 4) 30°.

43. Определитны сегментлысь площадьсӧ, хордаыс кӧ a ыджда, а дугаас: 1) 120°; 2) 90°; 3) 60°.

Веськыд визьясӧн да кытшвизь дугаясӧн ограничитӧм фигураяслӧн площадьяс.

44. Определитны ӧшиньлысь площадьсӧ (62ʼ чертёж), коді веськыднёльпельӧса формаа да кодлӧн вылысыс помасьӧ кругса 60° дугаӧн; ӧшиньлӧн судтаыс (дуга шӧрсянь подувтасӧдзыс) 2,4 м да пасьтаыс — 1,6 м.

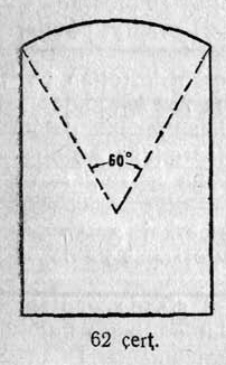
45. 1) r радиуса кытшвизь джынйӧс юкӧма 3 ӧтыджда юкӧнӧ да юкан чутъяссӧ ӧтлаалӧма диаметр помкӧд. Определитны кытшвизь джынлысь шӧр юкӧнса площадьсӧ.

2) CD дуга помъяс AB диаметр помъяссянь ӧтылнаынӧсь. Определитны площадь, коді CD дуга да AC да AD хордаяс костын, круглӧн кӧ площадьыс = Q да CD дугаын n°.

46. R радиуса кругын шӧр чутсянь ӧтарлабокас нуӧдӧма кык параллельнӧй хорда; на пиысь ӧтиыс стягивайтӧ 120°-а дуга, а мӧдыс — 60°-аӧс. Определитны круглысь хордаяскостса площадьсӧ.

47. Кык вомӧнассян кытшвизьлӧн ӧтувъя хордаыс a ыджда, коді ӧти кругас стягивайтӧ 60°-а дуга, а мӧдас — 90°-аӧс. Определитны кругъяслысь ӧтувъя площадь юкӧнсӧ (кык случай).

48. Круглӧн площадьыс = Q. Определитны сыӧ впишитӧм веськыднёльпельӧсалысь площадьсӧ, кодлӧн бокъясыс относитчӧны кыдз m : n.

49. R радиуса кругӧ впишитӧма веськыднёльпельӧсаӧс, кодлӧн площадьыс круг джын площадь ыджда. Определитны тайӧ веськыднёльпельӧсалысь бокъяссӧ.

50. Q площадя круг гӧгӧр опишитӧма 30° ыджда пельӧса ромбӧс. Определитны тайӧ ромблысь площадьсӧ.

51. Q площадя правильнӧй куимпельӧса гӧгӧр опишитӧма кытшвизьӧс да сійӧ жӧ куимпельӧсаӧ впишитӧма мӧд кытшвизьӧс. Определитны тайӧ кык кытшвизькостса кольчалысь площадьсӧ.

52. AMB лоӧ 120° ыджда дуга; OA да OB — радиусъяс; AC да BC — касательнӧйяс; DME лоӧ CA да CB костса да AMD дугаӧ касайтчысь C шӧр чутсянь нуӧдӧм дуга. Корсьны CDME да OAMB секторъяс площадьяслысь отношенньӧсӧ.

53. ACB дуга помъяссянь нуӧдӧма D чутын вомӧнассьытӧдз касательнӧйясӧс. Определитны DACB-лысь площадьсӧ, круглӧн кӧ радиусыс = R, а дугаын 1) 90°; 2) 120°; 3) 60°.

54. Ӧткузя бокъяса куимпельӧса шӧр чутсянь нуӧдӧма кытшвизь, коді куимпельӧсалысь бокъяссӧ вундӧ сідз, мый ортсыса дугаясыс лоӧны 90° ыдждаӧсь. Куимпельӧсалысь боксӧ a пыр пасйӧмӧн определитны пытшкӧс дугаяс да бокъясса шӧр вундӧгъяс костса площадьсӧ.

55. 1) Кымын пӧв ыдждӧ круглӧн площадьыс, кор диаметрсӧ ыдждӧдам 3 пӧв? Кымын пӧв площадьыс чинӧ, радиуссӧ кӧ ичӧтмӧдам 5 пӧв?

2) Кымын пӧв колӧ ичӧтмӧдны круглысь радиуссӧ, медым площадьыс ичӧтмас 4 пӧв? Кымын пӧв колӧ ыдждӧдны круглысь диаметрсӧ, медым площадьыс ыдждас 5 пӧв?

56. 1) Позьӧ-ӧ 50 мм диаметра водопроводнӧй трубаӧс вежны 25 мм диаметра кык трубаӧн? Ӧтыджда‐ӧ лоӧны ӧти ыджыд трубаыслӧн да кык ичӧт трубаыслӧн сеченньӧ площадьясыс?

57. 63ʼ чертёж вылын сетӧм веськыднёльпельӧсаын штрихуйтӧм юкӧныслысь корсьны площадьсӧ.

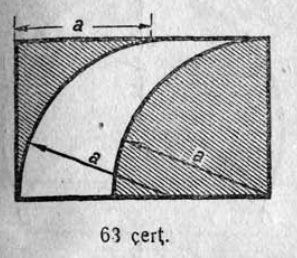
58. Сетӧм размеръяс серти определитны 64−67 чертёжъяс вылын сетӧм фигураяслысь площадьяссӧ.

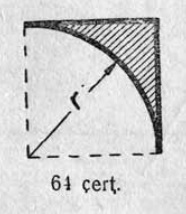
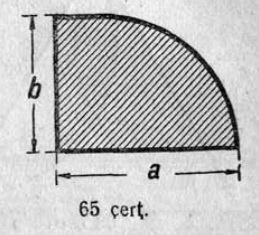
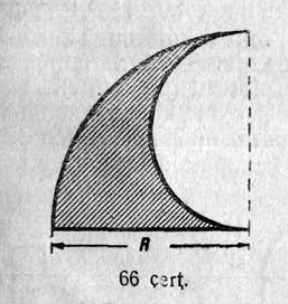
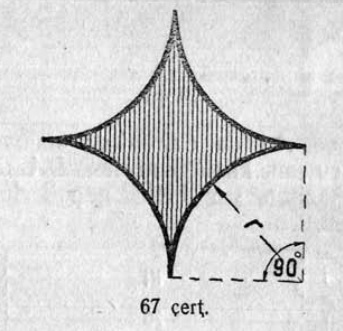
59. Кык ӧтыджда круг джынӧс пуктӧма мӧда-мӧдыс вылӧ сідз, мый налӧн диаметръясыс параллельнӧйӧсь, а кытшвизь джыныс ӧтиыслӧн мунӧ мӧд кытшвизьыс шӧр чут пырыс. Сетӧм круг джынъяслӧн радиусыс R ыджда. Определитны круг джынъясса ӧтувъя юкӧныслысь площадьсӧ.

60. Квадрат быд бок вылӧ, кыдз диаметр вылӧ, нуӧдӧма пытшкӧсланьыс кытшвизь джынъяс. Определитны артмӧм розеткалысь площадьсӧ, кор квадратлӧн бокыс a ыдждаӧсь.

61. Ромб бокъяс вылӧ, кыдз диаметръяс вылӧ, нуӧдӧма пытшкӧсланьыс кытшвизь джынъяс. Ромблӧн диагональясыс a да b. Определитны артмӧм розеткалысь площадьсӧ.

62. Диаметрӧс юкӧма ӧтыджда юкӧнъясӧ да кыкнан помсяньыс быд юкан чутӧдз нуӧдӧма кытшвизь джынъяс, та дырйи ӧти помсяньыс став кытшвизь джынъяссӧ нуӧдӧма вывланьӧ, а мӧдсяньыс ставсӧ увланьӧ. Докажитны, мый артмӧм кусыньтӧм визьясӧн кругыс юксис ӧтыджда юкӧнъясӧ да быд сэтшӧм юкӧнлӧн периметрыс кытшвизь кузя.

63. Ӧткузя бокъяса^Вуджӧдӧмын гижӧма "кык ӧткузя бока". — А.В./^ куимпельӧсаын быд кык йыв костӧд куимпельӧсаса шӧр чут пыр нуӧдӧма дугаяс (68‐ӧд чертёж). Куимпельӧсалӧн бокыс a ыджда. Определитны артмӧм розеткалысь площадьсӧ.

64. A да B чутъяс костӧд нуӧдӧма кык дуга, кодъяслӧн выпуклосьтъясыс видзӧдӧны ӧтарланьӧ; AMB дугаын 240°, ANB дугаын 120°. Тайӧ дугаясыс шӧръяскостса расстоянньӧыс a ыджда. Определитны луночкалысь площадьсӧ (69ʼ чертёж).

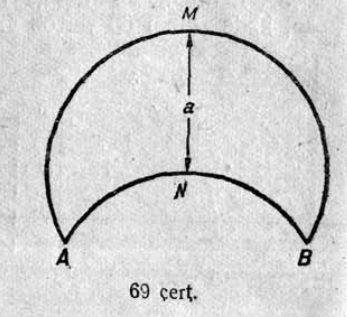
65. AB да CD — мӧда-мӧдыслы перпендикулярнӧй диаметръяс. D чутсянь, кыдз шӧр чутсянь, DA радиусӧн нуӧдӧма AMB дуга. Докажитны, мый AMBC луночка ABD куимпельӧсакӧд ӧтыджда.

66. Сетӧм кытшвизь джынвывса C чутысь AB диаметр вылӧ лэдзӧма CD перпендикулярӧс да AD да DB вундӧгъяс вылӧ вӧчӧма выль кытшвизь джынъяс (сетӧмыскӧд ӧтарвылӧ). Докажитны, мый куим кытшвизь джынкостса площадьыс CD диаметра круг площадь ыджда.

67. Артавны 70‐ӧд чертёж вылын штрихуйтӧм фигуралысь площадьсӧ. Размеръяссӧ сетӧма миллиметръясӧн.

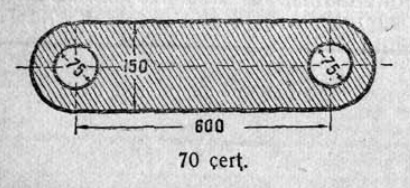
68. Артавны 71ʼ чертёж вылын мыччӧдлӧм сеченньӧлысь площадьсӧ. Размеръяссӧ сетӧма миллиметръясӧн.

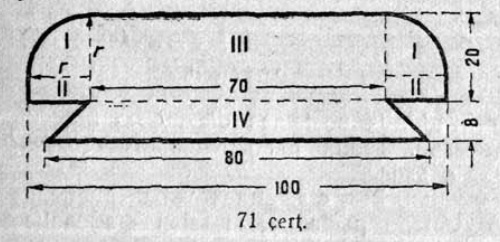
69. Определитны 72ʼ чертёж вылын мыччӧдӧм фасоннӧй кӧртлысь вомӧна сеченньӧ площадьсӧ.

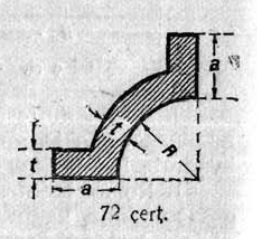
70. Кык параллельнӧй хорда 14 м да 40 м ыдждаӧс, на костса расстоянньӧыс 39 м. Определитны круглысь площадьсӧ.

71. Определитны сетӧм секторӧ впишитӧм круглысь радиуссӧ, секторлӧн кӧ радиусыс R ыджда да дугаас α градус [α = 1) 60°; 2) 90°; 3) 120°].

16 §. Алгебраӧс геометрияӧ приложитӧм. Средньӧй да крайньӧй отношенньӧӧн юкӧм.

Формулаясӧс стрӧитӧм.

1. 1) Стрӧитны ыджда вундӧгъясӧс.

2) 73ʼ чертёж вылын сетӧма: OA = AB = BC = CD = DE = EF = FG = GH = HK = KL = 1. Та дырйи AB ⊥ AO, BC ⊥ BO, CD ⊥ CO да с. в. Артавны: OB, OC, OD, OE, OF, OG, OH, OK, OL.

3) Стрӧитны:

ыджда вундӧгъяс.

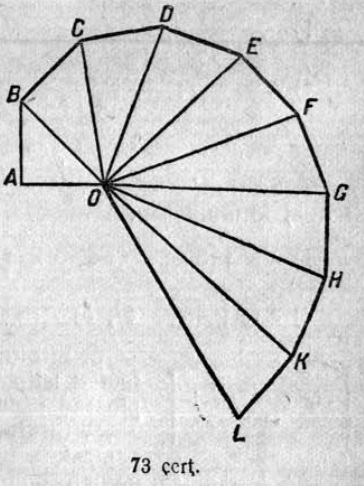
2. Вӧчны ыджда бокъяса куимпельӧсаӧс.

3. Индыны со кутшӧм выраженньӧяслысь измеренньӧсӧ, кодъяслӧн быд шыпас, π ӧтар, петкӧдлӧ вундӧглысь кузьтасӧ:

.

4. Кутшӧм формулаяс абу однороднӧйӧсь со кутшӧмъяс пиысь:

5. Восстановитны однородносьтсӧ со кутшӧм линейнӧй формулаясысь:^12‐ӧд номерын ӧпечатка оригиналын, вуж пассӧ колӧ вӧлі помавны водзджык. — А.В./^

6. Стрӧитны вундӧгъясӧс, кодъяс петкӧдлыссьӧны со кутшӧм рациональнӧй формулаясӧн:

7. Стрӧитны вундӧгъясӧс, кодъяс петкӧдлыссьӧны со кутшӧм иррациональнӧй формулаясӧн:

Фигураясӧс стрӧитӧм.

8. Вӧчны квадрат, медым сійӧ вӧлі сетӧм ӧткузя бокъяса куимпельӧсакӧд ӧтыджда (равновеликӧй). Куимпельӧсалӧн бокыс a ыджда.

9. Вӧчны круг, кодлӧн площадьыс медым вӧлі кык пӧв ыджыдджык сетӧм R радиуса круг площадьысь.

10. Сетӧм R радиуса кругӧс юкны шӧри концентрическӧй кытшвизьӧн.

11. Вӧчны квадрат, коді медым вӧлі a да h бокъяса параллелограмм ⅗ ыджда.

12. Вӧчны круг R да r радиусъяса концентрическӧй кытшвизьяскостса кольчакӧд ӧтыдждаӧс.

13. a подувтас да сы бердса 30° ыджда пельӧс серти вӧчны куимпельӧсаӧс, коді медым вӧлі сетӧм куимпельӧсакӧд ӧтыджда, кодлӧн подувтасыс b ыджда да судтаыс h ыджда.

Квадратнӧй уравненньӧлысь кореньяссӧ стрӧитӧм.

14. Стрӧитны кореньяссӧ квадратнӧй уравненньӧлысь: x² ± px ± q² = 0.

15. 1) AB вылын кыдз диаметр вылын (74‐ӧд чертёж) нуӧдӧма кытшвизь джын. Сетӧма: AB = p; BC ⊥ AB; BD = q; DE ∥ AB; EF ⊥ AB. Докажитны, мый AF да FB вундӧгъяс лоӧны x² − px + q² = 0 квадратнӧй уравненньӧлӧн кореньясӧн.

2) Видлалӧм построенньӧсӧ применитны x² − 6,5x + 4 = 0 квадратнӧй уравненньӧлысь кореньяссӧ стрӧитӧмӧ (уравненньӧсӧ решиттӧг).

3) Мый вӧсна тайӧ способсӧ x² − 2,5x + 9 = 0 уравненньӧӧ применитӧм оз сет колана результат?

Средньӧй да крайньӧй отношенньӧын юкӧм.

16. Сетӧм a вундӧгӧс юкны средньӧй да крайньӧй отношенньӧын, мӧд ногӧн: юкны сійӧс 2 юкӧнӧ сідз, медым ыджыдджык юкӧныс вӧлі средньӧй пропорциональнӧйӧн став вундӧгъяс да ичӧтджык юкӧн костас.

17. 1) Докажитны, мый правильнӧй вписаннӧй даспельӧсалӧн бокыс равняйтчӧ средньӧй да крайньӧй отношенньӧын юкӧм радиус ыджыдджык юкӧныслы.

2) Сетӧм R серти артавны a₁₀.

18. Кутшӧмкӧ вундӧгӧс кӧ юкӧма средньӧй да крайньӧй отношенньӧын, то ыджыдджык юкӧныс матыстӧмӧн лоӧ вундӧг ⅝ юкӧныс ыджда. Прӧверитны тайӧс да определитны татшӧм матыстӧмлысь точносьт степеньсӧ.

19. 1) Определитны вундӧглысь средньӧй да крайньӧй отношенньӧын юкигӧн ыджыдджык юкӧнсӧ, ичӧтджыкыс кӧ та дырйи b ыджда.

2) Средньӧй да крайньӧй отношенньӧын юкӧм вундӧглысь кӧ ичӧтджык юкӧнсӧ пуктыны ыджыдджык вылас, ыджыдджыкыс бара юксяс средньӧй да крайньӧй отношенньӧын. Докажитны.

20. Кытшвизьвывса чутсянь лэдзӧм перпендикулярӧн диаметр юксьӧма средньӧй да крайньӧй отношенньӧын. Кытшвизьлӧн радиусыс r ыджда. Корсьны перпендикулярлысь кузьтасӧ.

21. Докажитны, мый правильнӧй 5-пельӧсаын 2 вомӧнассян диагональ юксьӧны средньӧй да крайньӧй отношенньӧын.

22. Круглысь кӧ радиуссӧ юкны средньӧй да крайньӧй отношенньӧын да ыджыдджык юкӧннас нуӧдны концентрическӧй кытшвизь, сетӧм круглӧн площадьыс сідзжӧ юксяс средньӧй да крайньӧй отношенньӧын, та дырйи ыджыдджык юкӧныс лоӧ кольча. Докажитны тайӧс.

Алгебраическӧй методӧс применитӧм.

23. r радиуса круглысь диаметрсӧ нюжӧдӧм вылысь корсьны сэтшӧм чут, медым сысянь кругӧ нуӧдӧм касательнӧйыс вӧлі диаметрыс ыджда.

24. Сетӧм кытшвизь джынйӧ впишитны квадрат.

25. Сетӧма a подувтаса да h судтаа куимпельӧса. Впишитны сыӧ веськыднёльпельӧсаӧс, кодлӧн периметрыс 2p ыджда.

26. Сетӧм куимпельӧсаӧс юкны шӧри подувтасыслы параллельнӧй веськыд визьӧн.

27. Куимпельӧсалысь площадьсӧ юкны шӧри подувтасыслы перпендикулярнӧй веськыд визьӧн.

28. Сетӧм ромбӧ впишитны веськыднёльпельӧсаӧс, кодлӧн бокъясыс медым вӧліны ромб диагональясыслы параллельнӧйӧсь да площадьыс медым вӧлі ромб площадь ⅓ юкӧныс ыджда.

29. Сетӧм квадратӧ впишитны ӧткузя бокъяса куимпельӧсаӧс сідз, медым налӧн йывъясыс пиысь ӧти йыв вӧлі ӧтувъя.

30. a бока квадратӧ впишитны мӧд квадрат, кодлӧн бокыс b.

31. Вӧчны кытшвизьӧс, коді мед касайтчис r радиуса сетӧм кытшвизьӧ да сетӧм веськыд визьӧ сы вылын сетӧм чутын.

32. Сетӧма кык веськыднёльпельӧсаӧс, вӧчны коймӧдӧс, медым сійӧ вӧлі сетӧмъяс пиысь ӧтиыслы изопериметричнӧй, а мӧдыслы — ӧтыджда (равновеликӧй).

33. Сетӧм куимпельӧсаӧ впишитны веськыднёльпельӧсаӧс, кодлӧн медым подувтасыс относитчис судта дорас кыдз m : n.

34. ABCD параллелограммын AB бокыс a да BC — b. Нуӧдны EF веськыдӧс сідз, медым сійӧ вундіс ABCD-лы подобнӧй ABEF параллелограмм.

35. ABCD — параллелограмм. AB бокыс = a да BC = b. Нуӧдны EF веськыд, AB‐лы параллельнӧйӧс, сідз, медым сійӧ сетӧм параллелограммсӧ юкис кык подобнӧй параллелограммӧ.

36. Веськыднёльпельӧсаса 2 воча пельӧсӧ впишитны кытшвизьяс, кодъяс медым сідзжӧ касайтчисны мӧда-мӧдас.

37. А да B чутъяс пыр нуӧдны кытшвизь, коді медым сетӧм веськыд визьысь вундіс m кузя хорда.

ТЕРМИН ӦКТӦД

Телӧ — тело

Свойство — свойство

Форма — форма

Ыджда — размер

Сяр — шар

Пространство — пространство

Пространство юкӧн — часть пространства

Кузьта — длина

Пасьта — ширина

Судта — высота

Кызта — толщина

Веркӧс — поверхность

Гранича — граница

Визь — линия

Веськыд визь — прямая линия

Нюкыля визь — кривая линия

Горизонтальнӧй веськыд визь —

горизонтальная прямая линия

Вертикальнӧй веськыд визь —

вертикальная прямая линия

Луч — луч

Вундӧг — отрезок

Чегласьӧм визь — ломаная линия

Смешаннӧй визь — смешанная линия

Плоскӧй веркӧс — плоская поверхность

Нюкыля веркӧс — кривая поверхность

Фигура — фигура

Геометрическӧй образ — геометрический образ

Аксиома — аксиома

Теорема — теорема

Кытшвизь — окружность

Круг — круг

Шӧр чут — центр

Тупкӧса — замкнутый

Радиус — радиус

Хорда — хорда

Диаметр — диаметр

Дуга — дуга

Дуга градус — дуговой градус

Пельӧс градус — угловой градус

Минут — минута

Секунд — секунда

Ӧтыджда, равняйтчӧ — равно

Пельӧс — угол

Павтыртӧм пельӧс — развернутый угол

Веськыд пельӧс — прямой угол

Ёсь пельӧс — острый угол

Тшӧтшыд пельӧс — тупой угол

Шӧрса пельӧс — центральный угол

Йӧртӧм пельӧс — заключенный угол

Бердса пельӧс — прилежащий угол

Орчча пельӧс — смежный угол

Пополнительнӧй пельӧс — пополнительный угол

Дополнительнӧй пельӧс — дополнительный угол

Пытшкӧс пельӧс — внутренний угол

Ортсыса пельӧс — внешний угол

Паныда пельӧс — противоположный угол

Бок — сторона

Подувтас — основание

Йыв — вершина

Биссектриса — биссектриса

Медиана — медиана

Перпендикуляр — перпендикуляр

Пӧлыня визь — наклонная линия

Чут — точка

Проекция — проекция

Куимпельӧса — треугольник

Веськыд пельӧса куимпельӧса —

прямоугольный треугольник

Ёсь пельӧса куимпельӧса —

остроугольный треугольник

Тшӧтшыд пельӧса куимпельӧса —

тупоугольный треугольник

Разнӧй бокъяса куимпельӧса —

разносторонний треугольник

Кык ӧткузя бока куимпельӧса —

равнобедренный треугольник

Ӧткузя бокъяса куимпельӧса —

равносторонний треугольник

Катет — катет

Гипотенуза — гипотенуза

Осевӧй симметрия — осевая симметрия

Симметрия ось — ось симметрии

Параллельнӧй веськыд визьяс —

параллельные прямые линии

Пытшкӧс ӧтарбокса пельӧс —

внутренний односторонний угол

Ортсыса ӧтарбокса пельӧс —

внешний односторонний угол

Соответственнӧй пельӧс —

соответственный угол

Крестӧн куйлысь пельӧс —

накрест лежащий угол

Нёльпельӧса — четырехугольник

Трапеция — трапеция

Параллелограмм — параллелограмм

Квадрат — квадрат

Ромб — ромб

Диагональ — диагональ

Центральнӧй симметрия — центральная симметрия

Веськыднёльпельӧса — прямоугольник

Шӧр визь — средняя линия

Унапельӧса — многоугольник

Площадь — площадь

Ӧти нима — одноименный

Ӧтгырся — равновеликий

Ӧтыдждаысь вӧчӧма — равносоставленный

Геометрическӧй места — геометрическое место

Ӧтылнаын — равноудаленный

Касательнӧй визь — касательная линия

Касанньӧ чут — точка касания

Шӧр чут корсьысь — центроискатель

Вписаннӧй пельӧс — вписанный угол

Описаннӧй пельӧс — описанный угол

Отсасьысь — вспомогательный

Концентрическӧй кытшвизь —

концентрическая окружность

Пропорциональнӧй вундӧгъяс —

пропорциональные отрезки

Подобйӧ — подобие

Поперечнӧй масштаб — поперечный масштаб

Подобнӧя пукталӧм — подобно расположенные

Арталӧм — вычисление

Апофема — апофема

Сектор — сектор

Сегмент — сегмент