ГЕОМЕТРИЯЛӦН СИСТЕМАТИЧЕСКӦЙ КУРС

ПЫРТӦД

ОСНОВНӦЙ ГЕОМЕТРИЧЕСКӦЙ ВЕЖӦРТАСЪЯС.

1 §. Физическӧй да геометрическӧй телӧ.

Став ми гӧгӧрса предметъяслӧн, либӧ телӧяслӧн, эм ӧти сэтшӧм ӧтувъя аслыссикаслун, мый найӧ пространствоысь босьтӧны определённӧй юкӧн. Такӧд ӧттшӧтш быд предметлӧн эм аслыспӧлӧс уна физическӧй свойствояс, кодъяс серти сійӧ янсӧдчӧ мукӧд предметъясысь. Сэтшӧм физическӧй свойствоясӧн лоӧны: телӧлӧн сьӧкта, сылӧн масса, непроницаемосьт, упругосьт, рӧм (цвет) да мукӧд свойствояс, кодъяс зависитӧны телӧ веществоысь. Физическӧй свойствоясысь ӧтдор, быд телӧлӧн эмӧсь характернӧй ортсыс свойствояс: форма, ыджда (размер) да положенньӧ; тайӧ свойствояс шусьӧны телӧса геометрическӧй свойствоясӧн.

Телӧлысь физическӧй свойствояссӧ велӧдӧны естественнӧй наукаяс: физика, химия да с. в. Телӧлысь геометрическӧй свойствояссӧ, — формасӧ, ыдждасӧ да положенньӧсӧ, — кодъяс характернӧйӧсь быд предметлы да кодъяс серти предметъяс торйӧдчӧны мӧда-мӧдысь, велӧдӧ геометрия; та дырйи геометрия бокӧ вештӧ телӧяслысь физическӧй свойствояссӧ; та вӧсна геометрия велӧдысьлы, кор сійӧ тӧдмалӧ телӧяслысь форма да мукӧд геометрическӧй свойствояс, дзик ӧткодь босьтны кӧртысь куб либӧ мольыда шыльӧдӧм гранитысь куб, резинаысь шар либӧ лыысь тӧчитӧм шар, стеклӧысь призма либӧ пуысь призма да с. в.

Мед бурджыка тӧдмавны миян гӧгӧрса телӧяслысь формаяс, геометрия велӧдысьлы колӧ кужны ассьыс вниманньӧ кежӧдны телӧясса физическӧй свойствоясысь да велавны став вниманньӧсӧ чукӧртны сӧмын ӧти свойство вылӧ — телӧяс форма вылӧ.

Оз ков вунӧдны, мый збыльысьсӧ (действительносьтын) телӧлӧн формаыс янсӧдтӧмтор сійӧ свойствоясысь, да мый телӧлысь форма велӧдігӧн геометрия торйӧдӧ тайӧ формасӧ, вештӧ сійӧс тайӧ пространствоса збыльысьса телӧысь. Сӧмын зэв уна сё вося опытӧн морт велаліс мӧвпавны отвлечённӧй (янсӧдан) формаясӧн, тӧдмаліс налысь аслыссикаслунъяссӧ, кутіс кужны торъя формаяслысь свойствояс используйтны збыль олӧмас — техникаын, производствоын.

Сідзкӧ, геометрия оз велӧд физическӧй телӧсӧ став физическӧй свойствояснас, а велӧдӧ став физическӧй свойствояссьыс янсӧдӧм телӧӧс, кодлӧн кольӧма сӧмын формаыс, сідзкӧ и ыдждаыс тайӧ збыльысьса физическӧй телӧыслӧн, кодлысь мӧвпӧн янсӧдӧма, торйӧдӧма физическӧй свойствояссӧ. Татшӧм телӧяс шусьӧны геометрическӧй телӧясӧн. Сы вӧсна, мый быд физическӧй телӧ пространствоысь босьтӧ буретша (определённӧй) юкӧн, тась петӧ, мый геометрическӧй телӧ лоӧ физическӧй телӧӧн пространствоысь босьтан юкӧн, мӧд кывъясӧн кӧ шуны: геометрическӧй телӧ эм пространстволӧн гӧгӧрбок ограничитӧм юкӧн.

Геометрическӧй телӧлӧн сідз жӧ, кыдз быд физическӧй телӧлӧн, эм куим муртас: кузьта, пасьта да судта либӧ кызта. Телӧысь кӧ юкам мыйкӧ ыджда тор, сійӧ торйыс бара лоӧ телӧ. Сійӧ, мыйӧн телӧ торйӧдчӧ ас гӧгӧрса пространствоысь да мукӧд телӧясысь, шусьӧ сійӧ телӧса веркӧсӧн; телӧлӧн границаыс — веркӧсыс.

Ас гӧгӧрса обстановкаысь ми аддзывлам быдсяма нога веркӧсъяс, кодъяслӧн формаыс определяйтчӧ телӧ формаӧн. Сідз, класса дӧскалӧн, пызанлӧн, ведралӧн, мачлӧн, шарлӧн, цилиндрлӧн, конуслӧн веркӧсъясныс аслыссикасаӧсь да зависитӧны телӧ формаысь.

Телӧлысь веркӧссӧ позьӧ торйӧдны юкӧнъясӧ: быд юкӧныс сылӧн сідзжӧ лоӧ веркӧсӧн.

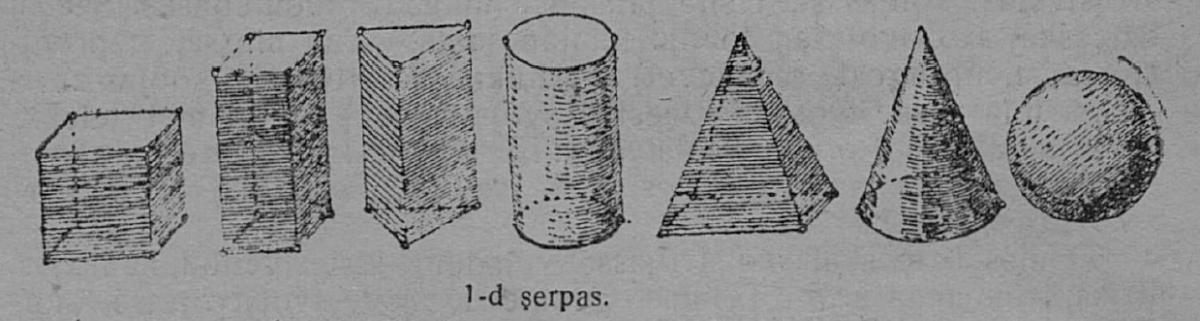
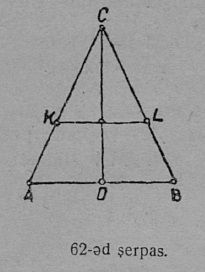
1 серпас вылын петкӧдлӧма различнӧй формаа телӧясӧс: куб, веськыдпельӧса параллелепипед, призма, цилиндр, пирамида, конус, шар. На костын ӧтикъяслӧн, — кублӧн, бруслӧн, призмалӧн, пирамидалӧн, — плоскӧй веркӧсныс; мукӧдлӧн, — шуам, шарлӧн, нюкыля веркӧс; коймӧд сикасъяслӧн — цилиндрлӧн да конуслӧн фигураясыс — ограничитӧма плоскӧй да нюкыля веркӧсъясӧн.

Веркӧслӧн эм кык муртас: кузьта да пасьта. Веркӧслӧн граница, мӧд ногӧн, сійӧ места, кӧн телӧса веркӧслӧн ӧти юкӧн вомӧнасьӧ мӧдкӧд, шусьӧ визьӧн. Веркӧслӧн границаыс визь. Визьлӧн эм сӧмын ӧти муртас — кузьта. 1 серпас вылысь видлалам куб. Кублӧн дорыш лоӧ кубса кык граньлӧн мӧда-мӧдкӧд вомӧнасян места; быд ӧти грань лоӧ кубса став веркӧслӧн юкӧн.

Визь позьӧ торйӧдлыны юкӧнъясӧ; та дырйи быд сэтшӧм юкӧн бара лоӧ визь.

Визьлӧн границаыс — чут. Чутлӧн некутшӧм муртас абу. Чут лоӧ сэтшӧм места, кӧн вомӧнасьӧны кык либӧ некымын визь. Сідз, кублӧн йыв (1 серпас) лоӧ куим визьлӧн вомӧнасянін места. Веркӧсъяс, визьяс да чутъяс позьӧ аддзыны сӧмын телӧяс вылысь; торйӧн найӧ овны оз вермыны; геометрияын кӧ ми сёрнитам веркӧсъяс, визьяс да чутъяс йылысь, кыдз торйӧн олысьяс йылысь, тайӧ сӧмын сы вӧсна, мый ми мӧвпалам найӧс телӧясысь юкӧмӧн, кыдз быттьӧ босьтӧмӧн.

Телӧ, веркӧс, визь да чут шусьӧны геометрическӧй образъясӧн.

2 §. Геометрическӧй образъяслӧн движенньӧӧн артмӧм.

Чутӧн пасйыссьӧ пространствоын определённӧй места, кӧть мед кӧн сійӧ эз вӧв: телӧ веркӧс вылын либӧ телӧ пытшкын, веркӧс вывті нуӧдӧм визь вылын либӧ телӧысь янасӧн мӧвпалан визь вылын.

Чут, кор сійӧ вешласьӧ (двигайтчӧ) пространствоын (2-д серп.), дугдывтӧг вежлалӧ ассьыс положенньӧ, да кыдз быттьӧ ас мунӧмнас гижтӧ кутшӧмкӧ визь, та вӧсна шуӧны: визь лоӧ мунысь чутлӧн туй. Биа ӧгырӧс кӧ, коді югъялан чут кодь, ӧдйӧ вештавны, сэки сетӧ представленньӧ визь йылысь, коді артмӧ кыдзи став торъя положенньӧяслӧн туй, кӧнъяс вӧлалӧ шом, кор сійӧ мунӧ пространствоын.

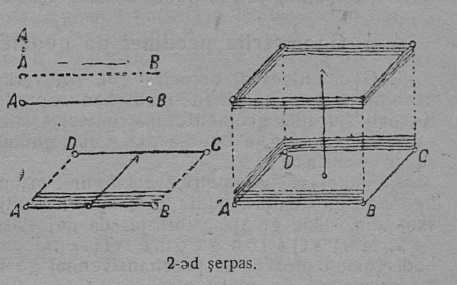
Сідз жӧ вермам представитны, мый веркӧс артмӧ пространствоын визь мунӧмӧн (2-д серп.), оз кӧ визьыс мун воддза ас направленньӧ кузяыс. Кор ӧдйӧ бергалӧ телега гӧгыль, сылӧн кӧльӧса паличьясыс быттьӧ ӧтлаасьӧны да быттьӧ артмӧдӧны поверхносьт.

Веркӧс мунӧмысь артмӧ телӧ, та дырйи мед сӧмын веркӧс эз мун воддза ас сулаланног направленньӧ кузяыс (2-д серпас).

Круглӧн диаметр гӧгӧр бергалӧм сетӧ шар йылысь представленньӧ.

3 §. Визьяслӧн да веркӧсъяслӧн сикасъяс.

1. Телӧяс вылын вермӧны лоны веськыд да нюкыля визьяс.

Сідз, кубса кык граньлӧн вомӧнасянін лоӧ сылӧн дорыш — веськыд визь; цилиндрлӧн бокса да подувтасса веркӧсъяслӧн вомӧнасяніныс кругкытш — нюкыля визь.

Веськыд визь йылысь урчитӧм сетны оз позь. Веськыд визь йылысь вежӧртас колӧ лыддьыны основнӧйӧн, тайӧ вежӧртассӧ морт босьтӧ веськыда быдлунъя опытысь.

Веськыд визь направленньӧлӧн особӧй случайяс лоӧны — горизонтальнӧй да вертикальнӧй веськыдъяс. Горизонтальнӧй веськыд визьлысь направленньӧ индӧ бедь, коді куйлӧ неыджыд ва веркӧс вылын; вертикальнӧй веськыдлысь направленньӧ корсьӧны сідз шуана отвесӧн, мӧд ног кӧ, шнурӧн, код помӧ кӧрталӧма ичӧтик гира. Вертикальнӧй веськыд визь лоӧ сэтшӧм веськыд, кодлӧн направленньӧ мунӧ му шӧрчутлань.

2. Телӧяслӧн веркӧсъяс юксьӧны кык сикасӧ: плоскӧй веркӧсъяс да нюкыля веркӧсъяс.

Плоскӧй веркӧсӧн, либӧ прӧста плоскосьтӧн ми шуам сэтшӧм веркӧс, кодкӧд веськыд визь вермӧ ӧтлаасьны любӧй направленньӧ кузя. Примерӧн плоскосьтлы вермас лоны бура шыльӧдӧм пызан пӧв; любӧй направленньӧ кузя сы вылӧ пуктӧм линейкалӧн дорыш топыда сибалӧ, весигтӧ югыд оз письт на костӧд.

Кублӧн граньяс, цилиндрлӧн да конуслӧн подувтасъяс — плоскосьтъяс. Шарлӧн веркӧс, цилиндрлӧн да конуслӧн бокса веркӧсъяс — нюкыля веркӧсъяс; шар веркӧс вылӧ пуктӧм линейкалӧн дорыш некутшӧм направленньӧын сыкӧд оз ӧтлаась; линейка дорыш кӧ пуктыны цилиндр либӧ конус веркӧс вылӧ, аддзам, мый сійӧ накӧд ӧтлаасьӧ оз быд направленньӧ кузя.

Горизонтальнӧй веркӧс пыдди босьтӧны ичӧтик доз пытшса ва веркӧс.

4 §. Геометрия предмет да геометрияӧс юкӧм.

1. Геометрическӧй образъяс: чут, визь, веркӧс, телӧ позьӧ видлавны быдӧнӧс торйӧн либӧ мӧда-мӧдыскӧд определённӧй сочетанньӧын. Кыкнан случайын геометрическӧй образъяс шусьӧны геометрическӧй фигураӧн, а фигураӧ пырысь быд геометрическӧй образ шусьӧ сійӧ элементӧн.

Куимпельӧса — геометрическӧй фигура, сылӧн доръяс да пельӧсъяс — фигуралӧн элементъяс, куимпельӧсалӧн элементъяс; куб — геометрическӧй телӧ, сылӧн граньяс, дорышъяс да пельӧсъяс — кублӧн элементъяс.

2. Мый сійӧ лоӧ геометрия? Геометрия — сэтшӧм наука, коді велӧдӧ плоскӧй да пространственнӧй геометрическӧй фигураяслысь признакъяс да свойствояс.

Плоскӧй фигураясӧн шусьӧны сэтшӧм фигураяс, кодъяс став ас элементъяснас расположитчӧны сӧмын ӧти плоскосьт серти; сідз, куимпельӧса, вомӧнасян кык веськыд визь, кытшвизь — плоскӧй фигураяс.

Пространственнӧй фигураясӧн шусьӧны сэтшӧм фигураяс, кодъяс став ас элементъяснас ӧти плоскосьт вылӧ оз вермыны тӧрны. Пространственнӧй фигураяслы, либӧ телӧяслы, примеръясӧн вермасны лоны кык вомӧнасян плоскосьт, куб, призма, цилиндр, шар да с. в.

Геометрия юксьӧ кык юкӧнӧ: планиметрияӧ, коді велӧдӧ плоскӧй фигураяслысь свойствояс, да стереометрияӧ, коді велӧдӧ пространственнӧй фигураяслысь, либӧ телӧяслысь свойствояс. Геометрия, кыдзи и быд наука, артмис наблюденньӧысь да опытысь да быдмис морт хозяйственнӧй потребносьтъяскӧд чорыда йитчӧмӧн. Кыв геометрия — греческӧй кыв, комиӧн лоӧ “му мурталӧм”.

3. Уна сё во сайын миян эраӧдз чужис геометрия. Асыввыв культурнӧй йӧзъяс, вавилоняна да египтяна, дӧза нин тӧдлісны геометриятӧ, сы вӧсна, мый налы ковмыліс муртавны му участокъяс, вӧчавны быдсяма постройкаяс да велӧдны небесаса светилӧяслысь ветлӧдлӧм. Водзӧ геометрия, кыдзи наука, кутіс паськавны Грецияын. Грецияса воддза математикъяс, египетса математикъяслӧн велӧдчысьяс, 6 сё во водз миян эраӧдз тӧдісны нин геометрическӧй фигураяслысь уна свойствояс; медпрӧстӧй геометрическӧй образъяс йылысь опытсьыныс босьтан тӧдӧмлун подувтас вылын урчитісны сложнӧйджык геометрическӧй образъяслысь свойствояс. Эвклидӧдз, коді оліс миян эраӧдз 3 сё во водз, геометрическӧй образъяс йылысь чукӧрмисны зэв уна тӧдӧмъяс; Эвклидлӧн зэв ыджыд заслуга, мый сійӧ ас сочиненньӧас (“Начала”) чукӧртіс ӧти системаӧ ставсӧ, мый сійӧ тӧдӧ вӧлі фигураяс да телӧяс свойствояс йылысь.

I. ВЕСЬКЫД ВИЗЬ

1 §. Веськыд визь. Луч. Вундӧг. Чегласьӧм визь. Нюкыля визь.

Веськыд визь став визьясысь медся прӧстӧй визь. Веськыд визь йылысь гӧгӧрвоӧм вермасны миянлы сетны зэлыда нюжӧдӧм сунис, выверитӧм линейкалӧн дорыш; пемыд комнатаӧ ичӧтик розьӧд пырысь шонді лучьяс мунӧны веськыд визь кузя.

Веськыд визьтӧ позьӧ мӧвпӧн помтӧг нюжӧдны кыкнанла дорас.

Веськыд визь унджыкысь пасйӧны латинскӧй алфавитса кык ыджыд шыпасӧн; шыпасъяссӧ пуктӧны мӧда-мӧдсянь некымын кост кольӧмӧн веськыд визьысь вылӧджык либӧ улӧджык. 3-д серп. вылын гижтӧма AB веськыд визь.

Кӧнкӧ AB веськыд вылын кӧ босьтам C чут, сійӧ C чутыс AB веськыд визьӧс юкас кык лучӧ: CA да CB (4-д серп.).

C чут лоӧ лучлӧн заводитчан либӧ петан чут, гижигӧн сійӧ пуктыссьӧ воддза местаӧ. Луч вермӧ помтӧг нюжавны сӧмын ӧтарланьӧ. Сідз, CA луч позьӧ нюжӧдны C чутсянь сӧмын шуйгаланьӧ; CB лучӧс — веськыдланьӧ. Сідзкӧ:

CA да CB кык луч, кодъяс петӧны ӧти C чутысь да кодъяслӧн направленньӧясыс мӧда-мӧдыслы мӧдараӧсь, вӧчӧны ӧти веськыд визь.

Веськыд визь вылын кӧ босьтны кык чут A да B, тайӧ чутъяс костса веськыдлӧн юкӧн шусьӧ вундӧгӧн. Вундӧг пасйыссьӧ кык ыджыд шыпасӧн, кодъясӧс пуктӧны визьтор помъясӧ: AB (5-д серп.) — веськыд визьлӧн вундӧг. Вель унаысь визьторсӧ пасйӧны ӧти ичӧт шыпасӧн, шуам a-ӧн, кодӧс пуктӧны шӧрас кымын вундӧг улӧ либӧ вылӧ; та дырйи “a” унджыкысьсӧ петкӧдлӧ вундӧглысь масштаб единицаясӧн босьтӧм кузьтасӧ.

Сэтшӧм визь, коді артмӧма веськыд вундӧгъясысь, но кодъяс оз куйлыны ӧти веськыд визь вылын, шусьӧ чегласьӧм визьӧн (6-ӧд серп.). Вундӧгъясыс, кодъясысь артмӧма чегласьӧм визь, шусьӧны сы бокъясӧн, либӧ звеноясӧн. Чегласьӧм визь пасйыссьӧ ыджыд шыпасъясӧн, кодъясӧс пукталӧны сійӧ бокъясыс помъясӧ, шуам, сетӧма чегласьӧм визь ABCDE.

Нюкыля визьӧн шуӧны сэтшӧм визь, кодлӧн абу ни ӧти веськыд визьтор (7 серп.).

Сора визьӧн шуӧны сэтшӧм визь, коді артмӧма веськыд вундӧгъясысь да нюкыля визь юкӧнъясысь (8 серп.).

2 §. Веськыд визьлӧн аксиомаяс.

1. Веськыд визьӧс позьӧ помтӧг нюжӧдны кыкнанла дорас.

Тайӧ свойствоысь ӧтдор, веськыд визьлӧн эмӧсь мукӧд свойствояс.

Плоскосьт вылын пасъям A да B кык чутлысь положенньӧ (9-ӧд серпас). Тайӧ A да B чутъяс пыр нуӧдам выверитӧм линейкаӧн веськыд визь. Тайӧ жӧ A да B чутъяс пыр пондам кӧ нуӧдны мӧд веськыд визь, аддзам, мый сійӧ воддзаыскӧд вевсяасяс; татысь петӧ мый:

2. Кык сетӧм чут пыр позьӧ нуӧдны веськыд визь и сӧмын ӧтиӧс.

Тайӧ лоӧ веськыд визьлӧн мӧд свойство, сійӧ петкӧдлӧ, мый быд веськыд визьлӧн положенньӧыс сполнӧя определяйтчӧ кык чутӧн; та вӧсна, кык веськыд визь кӧ ӧтлаавны сідз, мед ӧтик веськыд визьыслӧн кык чут ӧтлаасисны мӧд веськыд визь кык чуткӧд, сэки кыкнан веськыд визьыс ӧтвесьтасясны став чутъяснаныс. Кык веськыд визьлӧн кӧ эм сӧмын ӧти ӧтувъя чут, найӧ вомӧнасьӧны.

Вомӧнасян кык веськыд визьлӧн AB да CD ӧтувъя чут шусьӧ вомӧнасянін чутӧн.

Ӧти чут пыр позьӧ нуӧдны помтӧм уна веськыд визь. Став сэтшӧм веськыдъяслӧн совокупносьт шусьӧ веськыд визьяс позтырӧн.

Позтырса став веськыдъяслӧн ӧтувъя чут шусьӧ позтырса шӧрчутӧн (центрӧн).

Плоскосьт вылын кӧ босьтны кык чут A да B да на пыр нуӧдны веськыд, нюкыля да смешаннӧй визьяс, A да B чутъяс кутасны граничитны AB веськыд вундӧг, нюкыля визьлысь AGB юкӧн да лоӧны ACDEFB смешаннӧйлӧн помъясӧн (10-д серп.). Тыдалӧ, мый AB вундӧг дженьыдджык нюкыляса AGB юкӧнысь да ACDEFB сора визьысь, татысь:

3. Веськыдлӧн вундӧг кык чут костын медся дженьыд расстоянньӧ.

Веськыд визь тайӧ свойство серти кык чут костса расстоянньӧ век мурталӧны на пыр мунысь веськыд визь кузя.

Вундӧглӧн кузьта определяйтӧ пом чутъяс костысь расстоянньӧ.

4. Веськыд визьлӧн, кыдз геометрическӧй фигуралӧн, эмӧсь уна свойствояс. Тайӧ свойствояслысь веськыдлунсӧ установитӧма опытӧн, кодӧс войтыр чукӧртісны ас гӧгӧрса мирлысь явленньӧяс быд лун видзӧдӧмӧн да практическӧй могъяс решиталӧмӧн.

Геометрическӧй фигура свойствояс йылысь татшӧм сужденньӧяс, кодъясӧс установитӧма опытӧн да кодъясӧс босьтӧны докажиттӧг, шусьӧны аксиомаясӧн. Веськыд визь йылысь эмӧсь со кутшӧм сужденньӧяс — аксиомаяс:

1) веськыд визьӧс позьӧ помтӧг нюжӧдны кыкнанла дорӧ;

2) сетӧм кык чут пыр позьӧ нуӧдны веськыд визь и сӧмын ӧтиӧс;

3) веськыд вундӧг — медся дженьыд расстоянньӧ кык чут костын.

3 §. Вундӧгъясӧс ӧтластитӧм.

Веськыд визьяслысь кузьтаяс ӧтластитны оз позь; тадзсӧ сы вӧсна, мый веськыд визьясӧс позьӧ нюжӧдны ӧтарӧ и мӧдарӧ помтӧг. Ӧтластитавны мӧда-мӧдкӧд позьӧ сӧмын веськыд вундӧгъясӧс.

Ӧтластитны кык вундӧг — тӧдмавны, ӧтыдждаӧсь найӧ али абу; абу кӧ ӧтыдждаӧсь, кодыс на пиысь ыджыдджык. Вундӧгъясӧс ӧтластитӧм вӧчсьӧ ӧти вундӧгӧс мӧдыс вылӧ пуктӧмӧн.

Задача. Ӧтластитны мӧда-мӧдкӧд кык вундӧг AB да CD (11-д серп.).

Решитӧм. AB вундӧг пуктам СD вундӧг вылӧ сідз, мед A чут ӧтлаасяс C чуткӧд да AB вундӧг мед мунас CD вундӧг кузя. Сійӧ случайын, кор B чут ӧтлаасяс D чуткӧд — CD вундӧг помкӧд, AB да CD вундӧгъяс ӧтыдждаӧсь. Вундӧгъяслысь равенство гижӧны тадз: AB = CD.

B чут кӧ усьӧ CD вундӧгса E чутӧ, коді куйлӧ C да D чутъяс костын, AB вундӧг CD вундӧгысь ичӧтджык. Гижӧд: AB < CD.

B чут кӧ усьӧ нюжӧдӧм CD вундӧгыс вылӧ кутшӧмкӧ E чутӧ, AB вундӧг CD вундӧгысь ыджыдджык. Гижӧд: AB > CD.

4 §. Вундӧгъяс вылын действиеяс.

1. Задача. Содтыны AB да CD вундӧгъяс; вундӧгъяслысь кузьтаяссӧ сетӧма 12 серпас вылын.

Построенньӧ. Нуӧдам MN веськыд визь (13 серп.). Тайӧ веськыд вывса K чутсянь циркуль отсӧгӧн пуктам KL = AB вундӧг; сы бӧрын L чутсянь пуктам LP = CD вундӧг сідз, мед воддза вундӧглӧн L пом чут вӧлі мӧд вундӧглӧн начальнӧй чутӧн. KP вундӧг сетӧ AB да CD вундӧгъяслысь сумма. Гижӧд: AB + CD = KL + LP = KP.

2. Задача. AB вундӧгысь чинтыны CD вундӧг; вундӧгъяслысь кузьтаяссӧ сетӧма 14 серпас вылын.

Построенньӧ. MN веськыд визь кузя пуктам KL = AB вундӧг; та бӧрын L чутсянь мӧдара направленньӧлань пуктам LP = CD вундӧг; вундӧг KP = AB − CD.

3. Задача. AB вундӧг ыдждӧдны 5 пӧв, мӧд ног кӧ, босьтны сійӧс 5-ысь содтанлыдӧн.

Построенньӧ. MN веськыд визь кузя сетӧм AB вундӧг пуктам мӧда-мӧдкӧд орччӧн 5 пӧв. AF вундӧг = 5AB (15 серп.).

4. Задача. Сетӧма вундӧгъяс: a, b да c. Построитны вундӧг: x = 3a + 2b − 4c.

Произвольнӧя босьтӧм веськыд визь вылӧ пуктам 3a ыджда вундӧг, сы дінӧ содтам вундӧг 2b = b + b, сэсся нёльысь чинтам c вундӧг. Задача вермас лоны сӧмын сэк, кор 3a + 2b > 4c либӧ 3a + 2b = 4c. Бӧръя случайын x = 0.

5. Вундӧгӧс вундӧг вылӧ юкӧм, тшӧтш и ӧтгырся да абу ӧтгырся пайясӧ юкӧм лоӧ торйӧн видлалӧма.

5 §. Вундӧгъясӧс мурталӧм.

Вундӧг мурталӧмыд лоӧ — тӧдмавны, кымын пӧв сэтчӧ тӧрӧ мӧд вундӧг, кодӧс босьтӧма единица пыдди. Вундӧгъясӧс мурталан единицаӧн вермас лоны кутшӧм колӧ вундӧг. Но век вундӧгъяс мурталӧны лӧсьӧдӧм кузьта мераясӧн: метрӧн, сантиметрӧн, миллиметрӧн.

Мед муртавны AB вундӧг, сы кузя пукталӧны бӧрйӧм линейнӧй единица. AB вундӧгӧ кӧ бӧрйӧм линейнӧй единицаыс пуктыссьӧ тыр пӧв, артмӧм лыд мыччӧдлӧ, кымын линейнӧй единица кузя лоӧ вундӧгыс. AB вундӧгӧ кӧ бӧрйӧм линейнӧй единицаыс пуктыссьӧ кымыныськӧ быдсаӧн да вундӧгысь нӧшта кольӧ кутшӧмкӧ коляс, колӧ артмӧм коляссӧ муртавны ичӧтджык линейнӧй мераӧн; лоас кӧ бара коляс, сійӧс ковмас муртавны нӧшта ичӧтджык мераӧн да с. в.

Вермас лоны, мый бӧрйӧм линейнӧй мераяс пиысь, а сідзжӧ и найӧ юкӧнъясыс пиысь ньӧти оз пуктыссьы быдса лыд пӧв; сэк вундӧглӧн кузьта тӧдмавсьӧ матыстӧмӧн кыдз позьӧ стӧчджыка. 16 серпас вылын AB вундӧг 6,5 см.-ысь ыджыдджык, а 7 см.-ысь ичӧтджык; матыстӧмӧн сійӧ лоӧ 6,7 см. ыджда. Гижӧд: AB ≈ 6,7 см.

6 §. Кытшвизь да круг.

1. Кытшвизь да круг. Плоскосьт вылын кӧ OA вундӧг кутшӧмкӧ ӧти ас пом гӧгӧрыс, шуам O гӧгӧрыс, быдсаысь гӧгӧртас да бӧр воас воддза положенньӧас, A чут гижтас нюкыля визь, кодӧс шуӧны кытшвизьӧн. Плоскосьтлӧн кытшвизьӧн ограничитӧм юкӧныс шусьӧ кругӧн (17 серп.). O чут, код гӧгӧр OA вундӧг гӧгӧртӧ, шусьӧ кытшвизьлӧн да круглӧн шӧрчутӧн; OA вундӧг шусьӧ радиусӧн да пырджык пасйыссьӧ r либӧ R шыпасъясӧн.

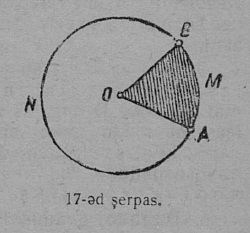
Колӧ индыны, мый OA вундӧглӧн оз сӧмын помсьыс A чут гижты кытшвизь; кор OA вундӧг гӧгӧртӧ O чут гӧгӧр, сылӧн любӧй чут гижтӧ кытшвизь.

Кытшвизьлӧн любӧй чут ӧтылнаын сулалӧ кытшвизь O шӧрсяньыс: тайӧ ылнаыс — радиуслӧн кузьтаыс. Гижӧд: OA = OB = r.

Кытшвизь построенньӧысь веськыда петӧ, мый кытшвизь лоӧ плоскосьт вылын сэтшӧм тупкӧса нюкыля визь, кодлӧн став чутыс ӧтылнаын ӧти чутсянь — шӧрчутсянь.

Кытшвизь дзикӧдз определитчӧ, кор сетӧма сылысь радиус да шӧрчутлысь положенньӧ.

Кытшвизьяс мӧда-мӧдысь торъялӧны ас радиус кузьтананыс; кымын ыджыд радиус, сымын ыджыд кытшвизь. Кык кытшвизь, кодъяслӧн сійӧ жӧ ӧти радиус, мӧда-мӧд вылӧ пуктігӧн, вевсяасьӧны; сідзкӧ, найӧ ӧтыдждаӧсь. Кытшвизь гижтӧны циркуль отсӧгӧн.

2. Дуга. Кор AB вундӧг O чут гӧгӧр вӧчас быдса гӧгӧртӧмлысь сӧмын юкӧн, сылӧн помыс, A чут, гижтас кытшвизьлысь юкӧн; кытшвизьлӧн юкӧн шусьӧ дугаӧн; круглӧн юкӧн, шуам, AOB, кодӧс гижтӧ OA вундӧг, шусьӧ секторӧн. AOB — сектор (17 серпас). “Дуга” кыв гижигӧн вежӧны татшӧм пасӧн ‿. Гижӧд ‿AB лыддьыссьӧ: AB дуга. Кор ми кытшвизь вылысь индам кутшӧмкӧ кык чут, шуам, A да B, сэк ми кытшвизь юкам кык пельӧ, кык дугаӧ, кодъяс унджыкысьсӧ оз овлыны ӧтыдждаӧсь. Медым точнӧя индыны, кык дуга пиысь кодыс йылысь мунӧ сёрни, пасйӧны сійӧс оз кык шыпасӧн, а куимӧн, ӧтиӧс на пиысь пуктӧны дуга помъяссӧ индысь шыпасъяс костӧ; гижӧны: ‿AMB (17 серп.). Кор абу индӧма, кытшвизьса ыджыдджык али ичӧтджык AB дуга йылысь мунӧ сёрни, сэк сійӧс пасйӧны сӧмын кык шыпасӧн: ‿AB, дзоляджык дугаӧс тадзсӧ век гӧгӧрвоӧмӧн.

Ӧти сійӧ жӧ кытшвизьлӧн либӧ кык ӧтыджда кытшвизьлӧн кык дуга ӧтыдждаӧсь сэк, кор найӧс мӧда-мӧд вылӧ пуктігӧн налӧн помъясса чутъяс ӧтлаасясны. Сідз, AB дугаӧс CD дуга вылӧ (18 серп.) пуктігӧн A чут воас D чутӧ, а B чут — C чутӧ, ‿AB = ‿DC.

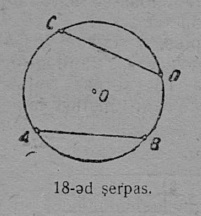
3. Хорда. CD вундӧг, коді ӧтлаалӧ кытшвизь вывса кык чут, шусьӧ хордаӧн; хорда стягивайтӧ дугасӧ; кытшвизьса быд хордалы соответствуйтӧ определённӧй дуга; сідз жӧ мӧдарӧ. Хорда юкӧ кытшвизь кык пельӧ (18 серпас). Хорда, коді мунӧ шӧрчут пыр, шусьӧ диаметрӧн. Кытшвизьын позьӧ нуӧдны помтӧм уна диаметр. Кытшвизлӧн диаметръяс ставыс ӧтыдждаӧсь; быд диаметр кык радиус ыджда. Диаметрӧн кытшвизь юксьӧ кык кытшвизь джынйӧ, а круг — кык круг джынйӧ.

Ӧти сійӧ жӧ кытшвизьын либӧ кык ӧтыдждаясын ӧтыджда дугаясӧн стягивайтчӧны ӧтыджда хордаяс. Тадзсӧ сы вӧсна, мый AB да CD дугаяс мӧда-мӧд вылӧ пуктігӧн кӧ ӧтлаасьӧны, ӧтлаасясны налӧн пом чутъяс, а сідзкӧ ӧтлаасясны AB да CD хордаяс, кодъяс ӧтлаалӧны дугаяслысь помса чутъяссӧ. Сідзжӧ лоӧ вернӧй сужденньӧ, мый дугаяс ӧтыдждаӧсь сэк, кор налы соответствуйтысь хордаяс ӧтыдждаӧсь.

4. Дугӧвӧй градус. Кытшвизь юкӧны 360 ӧтыджда юкӧнӧ, 360 ӧтыджда дугаӧ; быд сэтшӧм дуга шусьӧ дугӧвӧй градусӧн да пасйыссьӧ ичӧтик гӧгыльӧн, кодӧс пуктӧны дугалысь градус лыд индысь лыд веськыд вылӧ; сідз 360°, либӧ 180°, либӧ 90°. Кытшвизьын 360°, кытшвизь джынын 180°, кытшвизь нёльӧд юкӧнын 90°.

Быд дугӧвӧй градус юкӧны 60 ӧтыджда юкӧнӧ; быд татшӧм юкӧн шусьӧ дугӧвӧй минутӧн; дугӧвӧй минут пасйыссьӧ ’ пасӧн. Гижӧд: 30’ лыддьыссьӧ: 30 минут.

Быд дугӧвӧй минут юкӧны 60 ӧтыджда юкӧнӧ; быд татшӧм юкӧн шусьӧ дугӧвӧй секундӧн; дугӧвӧй секунд пасйыссьӧ ’’ пасӧн. Гижӧд 45’’ лыддьыссьӧ: 45 секунд. Гижӧд: 90°30’20’’ лыддьыссьӧ 90 градус 30 минут 20 секунд.

II. ПЕЛЬӦСЪЯС.

1 §. Пельӧс да сійӧс пасйӧм.

1. Кык луч OA да OB, кодъяс петӧны ӧти сійӧ жӧ O чутысь, мӧда-мӧдысь торйӧдчӧны направленньӧӧн да вӧчӧны фигура, кодӧс шуӧны пельӧсӧн (19 серп.).

O чут шусьӧ пельӧс йылӧн, OA да OB лучьяс — пельӧс бокъясӧн.

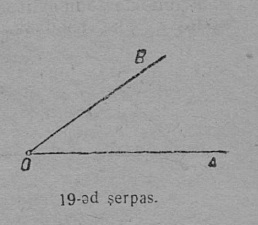
Унджыкысь пельӧсӧс пасйӧны куим ыджыд шыпасӧн, на костысь ӧтиӧс пуктӧны пельӧс йыв бердӧ, а мӧд кыксӧ пельӧс бокъяс вылӧ. Кыв “пельӧс” гижигӧн вежӧны пасӧн ∠; пельӧс йыв бердса шыпас гижӧны да лыддьӧны мукӧд кык шыпас костын.

OA да OB лучьясысь артмӧм пельӧс позьӧ гижны кык ног: либӧ ∠AOB либӧ ∠BOA. Унаысь пельӧс пасйӧны ӧти шыпасӧн, кодӧс пуктӧны йыв бердӧ; тадз овлӧ сэк, кор сійӧ жӧ йылын абуӧсь мукӧд пельӧсъяс. Сідзжӧ пельӧс пасйӧны латинскӧй либӧ греческӧй алфавитса ӧти ичӧт шыпасӧн либӧ лыдпасӧн; тадз пасйигӧн шыпас либӧ лыдпас гижӧны пельӧс пытшкӧсӧ (20 серпас). Унаысь пельӧс пытшкӧсті бокъяс костті нӧшта нуӧдӧны дуга, мед индыны, мый сёрни мунӧ сійӧ пельӧс йылысь, коді артмӧма сійӧ кык лучӧн, кодъяс костті нуӧдӧма дугасӧ.

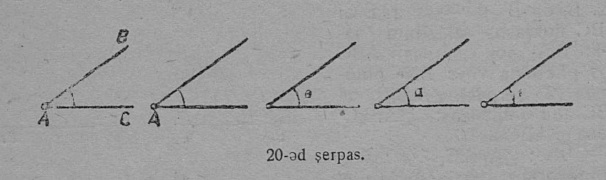
2. Видзӧдлам OA луч, коді бергалӧ O помыс гӧгӧр (21 серп.). Бергӧдчигас OA луч дугдывтӧг вежлалӧ ассьыс положенньӧсӧ, первоначальнӧй петан положенньӧысь вуджӧ выль OB положенньӧӧ да та дырйи гижтӧ ∠AOB.

Пельӧс лоӧ ас начальнӧй чут гӧгӧрыс луч бергӧдчӧмлӧн мера.

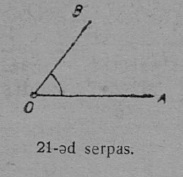
Пельӧс петкӧдлӧ луч кык направленньӧ кост разносьт — начальнӧй да конечнӧй направленньӧ костса разносьт.

3. Кык вомӧнасян AB да CD веськыдъяс мӧда-мӧдлы пӧлыняӧсь да вӧчӧны нёль пельӧс; быд тайӧ пельӧслӧн ыдждаыс сы сайын, ёна-ӧ ӧти веськыдыс пӧлыня мӧдыс серти.

Лӧсьӧдчӧмаӧсь шуны: пельӧс определяйтӧ, ёна-ӧ ӧти веськыд визь пӧлыня мӧд веськыд визь серти.

Пельӧслӧн ыджда оз зависит бокъясыс кузьтаысь.

2 §. Пельӧсъясӧс ӧтластитӧм. Пельӧсъяслӧн равенство да неравенство.

1. Сетӧма кык пельӧс: ∠ABC да ∠A₁B₁C₁ (22 серп.). Медым найӧс ӧтластитны да тӧдмавны, ӧтыдждаӧсь-ӧ найӧ али абу да, абу кӧ ӧтыдждаӧсь, кодыс на пиысь ыджыдджык, пуктӧны найӧс мӧда-мӧд вылӧ.

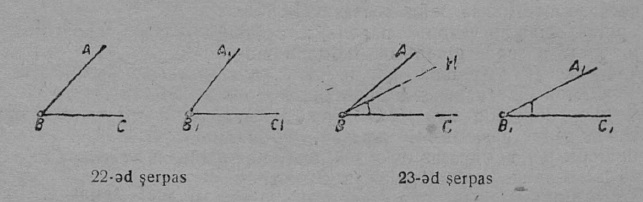
Пуктам (мӧвпалӧмӧн) ∠A₁B₁C₁ ∠ABC вылӧ сідз, мед B₁ йыв усьӧ B йылӧ, B₁C₁ бокыс мунас мӧд пельӧсса BC бок вывті; та дырйи кӧ B₁A₁ бок мунас BA бок вывті, ∠A₁B₁C₁ ӧтлаасяс ∠ABC-кӧд; сідзкӧ, пельӧсъяс сэк лоӧны ӧтыдждаӧсь. Гижӧд: ∠A₁B₁C₁ = ∠ABC.

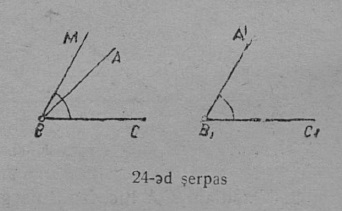
2. B₁ да B йывъясӧс да B₁C₁ да BC бокъясӧс ӧтлаӧдӧм бӧрын кӧ B₁A₁ бок мунас ABC пельӧс пытшті да воас BN положенньӧӧ (23 серпас), ∠A₁B₁C₁ да ∠ABC абу ӧтыдждаӧсь: ∠A₁B₁C₁ ичӧтджык ∠ABC-ысь.

Гижӧд: ∠A₁B₁C₁ < ∠ABC.

Медбӧрын, кор ∠A₁B₁C₁-ӧс ∠ABC вылӧ пуктігӧн B₁A₁ мунас ∠ABC ортсы да босьтас положенньӧ BM (24 серпас), ∠A₁B₁C₁ ыджыдджык ∠ABC-ысь.

Гижӧд: ∠A₁B₁C₁ > ∠ABC.

3 §. Павтыртӧм да веськыд пельӧс.

1. ∠ABC-лӧн (25 серпас) ыдждаыс бокъясыс пӧлыньлун сайын. Пельӧслысь кодкӧ боксӧ кӧ, шуам BA, бергӧдлыны B йыв гӧгӧр, а мӧд боксӧ BC эновтны вӧрзьӧдтӧг, BA бок кутас водзысь-водзӧ босьтавны положенньӧяс: BA₂, BA₃ да с.в. BA бок вермас босьтны сэтшӧм положенньӧ BA₁, мый лоӧ BC боклӧн нюжӧдӧм; татшӧм положенньӧ дырйи ∠A₁BC шусьӧ павтыртӧм пельӧсӧн.

Сідзкӧ, павтыртӧм пельӧс лоӧ сэтшӧм пельӧс, кодлӧн бокъяс вӧчӧны ӧти веськыд визь да пельӧс йывсяньыс ӧт-мӧдарӧ мунӧны.

Став павтыртӧм пельӧсъяс ӧтыдждаӧсь.

Мый тайӧ тадз, прӧверитӧны ӧти павтыртӧм пельӧсӧс мӧд вылӧ пуктӧмӧн.

Павтыртӧм пельӧс вылӧ позьӧ видзӧдны кыдз OA луч первоначальнӧй да конечнӧй направленньӧяс костса разносьт вылӧ, кор OA луч ас начальнӧй O чут гӧгӧр вӧчӧ быдса гӧгӧртӧмлысь джын (26 серп.).

2. Павтыртӧм пельӧслӧн джын шусьӧ веськыд пельӧсӧн.

Веськыд пельӧс пасйӧны латинскӧй ичӧт шыпасӧн d (французскӧй кывлӧн “droit” воддза шыпас; кыв “droit” — комиӧн “веськыд”).

Став веськыд пельӧсъяс мӧда-мӧдкӧд ӧтыдждаӧсь.

Веськыд пельӧс эм кытшвизь нёльӧд юкӧн вӧчысь OA лучлӧн начальнӧй да конечнӧй направленньӧяс костса разносьт (27 серп.): ∠AOB = d.

3. Кор OA луч ас начальнӧй O чут гӧгӧр вӧчас быдса гӧгӧртӧм да бӧр босьтас ассьыс первоначальнӧй положенньӧ, сэк шуӧны, мый OA луч гижтіс быдса пельӧс (28 серпас).

Веськыд пельӧс павтыртӧм пельӧс джын ыджда, та вӧсна павтыртӧм пельӧс кык веськыд пельӧс ыджда.

Гижӧд: ∠AOA₁ = 2d (26 серпас).

Быдса пельӧс кык павтыртӧм пельӧс ыджда, либӧ нёль веськыд пельӧс ыджда; быдса пельӧс 4d ыджда.

4. Пельӧс, коді артмӧма лучысь, кор сійӧ ас начальнӧй чут гӧгӧр гӧгӧртӧма нёльӧд юкӧнысь этшаджыка, веськыд пельӧсысь ичӧтджык да шусьӧ ёсь пельӧсӧн (21 серпас); веськыд пельӧсысь ыджыдджык, а павтыртӧмысь ичӧтджык, пельӧс шусьӧ тшӧтшыд пельӧсӧн (29 серпас).

5. Веськыд пельӧс босьтӧны пельӧс мера единица пыдди.

Пельӧсъяслысь ыджда петкӧдлӧны веськыд пельӧс юкӧнъясӧн. Сідз:

1) 0,3d; d/2; 2d/3 — ёсь пельӧсъяс: на костысь быд пельӧс веськыдысь ичӧтджык;

2) 1,5d; 5d/4; 11d/8 — тшӧтшыд пельӧсъяс: на костысь быд пельӧс веськыдысь ыджыдджык, а павтыртӧмысь ичӧтджык.

3) 2,3d; 11d/4; 23d/8 да с. в. — павтыртӧм пельӧсысь ыджыдджык пельӧсъяс.

4 §. Центральнӧй пельӧс да сылӧн свойствояс.

1. OM луч, кор сійӧ ас начальнӧй O чут гӧгӧр бергӧдчӧ, гижтӧ ∠MOM₁ (30 серп.), OM луч вылын босьтӧм кутшӧмкӧ A чут OM лучкӧд ӧттшӧтш мунігӧн гижтӧ AB дуга кытшвизьлысь, кодлӧн радиус OA ыджда. Видзӧдлам ∠AOB; сылӧн O йыв куйлӧ кытшвизь шӧрчутын, сылӧн бокъясыс лоӧны OA да OB радиусъяс, сійӧ бокъяс костӧ йӧртӧма сійӧ жӧ кытшвизьлысь AB дуга.

Пельӧс, кодлӧн йыв кытшвизь шӧрчутын, шусьӧ центральнӧй пельӧсӧн. Быд центральнӧй пельӧслы соответствуйтӧ определённӧй дуга. Гӧгӧрвоана, мый быд дугалы соответствуйтӧ определённӧй центральнӧй пельӧс, коді артмӧ, кор дугалысь помъяс радиусъясӧн ӧтлаалам шӧрчуткӧд.

2. Центральнӧй пельӧсъяслӧн да налы соответствуйтысь дугаяслӧн эмӧсь со кутшӧм свойствояс.

Ӧти сійӧ жӧ кытшвизьын либӧ ӧтыджда кытшвизьясын:

1) ӧтыджда центральнӧй пельӧсъяслы соответствуйтӧны ӧтыджда дугаяс;

2) ӧтыджда дугаяслы соответствуйтӧны ӧтыджда центральнӧй пельӧсъяс.

Сетӧма O чутын шӧрчута круг (31 серпас) да кык ӧтыджда центральнӧй пельӧсъяс: ∠AOB да ∠COD. Бергӧдам AOB сектор O шӧрчут гӧгӧр сідз, мед OA радиус ӧтлаасяс OD радиускӧд, сэк сы вӧсна, мый AOB да COD пельӧсъяс ӧтыдждаӧсь, OB радиус ӧтлаасяс OC радиускӧд, ӧтлаасясны AOB да COD секторъяса дугаяслӧн помса чутъяс A да D, B да C; дугаяслӧн кӧ помса чутъяс вевсяасясны, вевсяасясны сідзжӧ AB да CD дугаяс.

Гижӧд: кор ∠AOB = ∠COD, сэк ‿AB = ‿CD.

Ӧтыджда дугаяс да налы соответствуйтысь пельӧсъяс йылысь сужденньӧ гижсяс тадз: кор ‿AB = ‿CD, сэк ∠AOB = ∠COD.

Тайӧ сужденньӧ йылысь справедливосьт прӧверитны воддза ногӧн жӧ. Вывод сідзжӧ лоӧ справедливӧй дугаяс йылысь, кодъяс соответствуйтӧны ӧткодь радиуса кык различнӧй кытшвизьса ӧтыджда центральнӧй пельӧсъяслы.

3. Кытшвизьӧс 360 ӧтыджда юкӧнӧ юкӧм бӧрын да быд юкӧн чут шӧрчуткӧд ӧтлаалӧм бӧрын миян лоӧ 360 центральнӧй пельӧс, кодъяс мӧда-мӧдкӧд ставныс ӧтыдждаӧсь сы вӧсна, мый быдлы соответствуйтӧ кругкытшысь 1/360 юкӧн ыджда дуга, либӧ ӧти дугӧвӧй градус ыджда дуга.

Центральнӧй пельӧс, кодлы соответствуйтӧ ӧти градуса дуга, шусьӧ пельӧс градусӧн. Пельӧс градус юксьӧ 60 пельӧс минутӧ; быд пельӧс минут — 60 пельӧс секундӧ. Пельӧс градус да сылысь юкӧнъяс — минутъяс да секундъяс — дженьыда гижӧм вылӧ пасъяс сэтшӧмӧсь жӧ, кутшӧмӧсь дугӧвӧй градус да сылысь юкӧнъяс пасйӧм вылӧ.

Кытшвизьлӧн кӧ дугаын, шуам, ‿AB (32 серп.), 10° (дугӧвӧй), сылы соответствуйтысь центральнӧй пельӧсын 10° (пельӧс градус).

Вывод. Центральнӧй пельӧслы соответствуйтысь дугалӧн дугӧвӧй градус лыд ӧттшӧтш петкӧдлӧ пельӧслысь пельӧс градус лыд.

Шӧрчутын O йыла быдса пельӧс торйӧдчӧ 360 центральнӧй пельӧсӧ, 360°-ӧ. Павтыртӧм пельӧс ыджда центральнӧй пельӧсын 180°. Павтыртӧм пельӧс джын ыджда центральнӧй пельӧсын 90°.

Сідз, павтыртӧм пельӧслӧн джынйыс 90° ыджда, но павтыртӧм пельӧслӧн джынйыс эм веськыд пельӧс, сідзкӧ веськыд пельӧсын 90°, та вӧсна ӧти пельӧс градус лоӧ веськыд пельӧслӧн 1/90 юкӧн.

4. Веськыд пельӧс юкӧнъясӧн сетӧм пельӧсӧс градуснӧй мераӧ вуджӧдан таблица:

Веськыд пельӧс юкӧнъясӧн пельӧс	d/3	d/2	2d/3	3d/4	4d/5	d	4d/3	1,5d	5d/3	2d	3d	4d
Градуснӧй мераӧн пельӧс	30°	45°	60°	67°30’	72°	90°	120°	135°	150°	180°	270°	360°

5 §. Транспортир.

1. Пельӧс мурталӧм вылӧ пӧльзуйтчӧны особӧй приборӧн — транспортирӧн. Транспортир — круг джын, кодлысь дугасӧ юкӧма 180 дугӧвӧй градусӧ; круг джынлӧн шӧрчут пасйыссьӧ ичӧтика вундыштӧмӧн (33 серп.).

Мед муртавны сетӧм пельӧс, пуктӧны сы вылӧ транспортир сідз, мед сылӧн шӧрчут ӧтлаасяс пельӧс йывкӧд, а диаметр ӧтлаасяс пельӧс кык бок пиысь кодыскӧдкӧ ӧтиыскӧд, да видзӧдӧны, транспортир вывса кутшӧм юкӧнӧд мунӧ пельӧслӧн мӧд бок; лыд, кодӧс пуктӧма транспортир юкӧнӧ, код пыр мунӧ пельӧслӧн мӧд бок, петкӧдлӧ, кымын градус мурталан пельӧсын.

Транспортирӧн пӧльзуйтчӧм подувтасьӧ сы вылын, мый быд центральнӧй пельӧслы соответствуйтӧ дуга, кӧн сы мында жӧ быдса градус да сылӧн юкӧнъяс, мыйта центральнӧй пельӧсын.

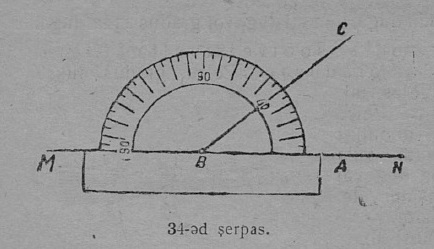
2. Транспортирӧн сідзжӧ позьӧ вӧчны пельӧс. Та вылӧ нуӧдӧны веськыд визь MN (34-ӧд серпас); сы вылӧ пуктӧны транспортир сідз, мед сылӧн диаметр ӧтлаасяс веськыд визькӧд; пасйӧны пельӧслысь йыв транспортир шӧрчутӧ; нуӧдӧны веськыд визь шӧрчут да транспортирса юкӧм чут пыр; артмӧ колана пельӧс.

3. Кытшвизьлӧн кузьта зависитӧ радиус кузьтаысь; кымын ыджыд радиус, сымын ыджыд лоӧ кытшвизь; татысь тыдалӧ, мый ӧти дугӧвӧй градуслӧн кузьта, мӧд ног кӧ, кытшвизьлӧн 1/360 юкӧн, зависитӧ радиусысь да вежласьӧ радиус вежсьӧмысь. Тадз оз ло пельӧс градус вӧчигӧн. Пельӧс градус радиус кузьтаысь оз зависит; пельӧс градус — вежласьтӧм, постояннӧй величина; сійӧ веськыд пельӧс 1/90 юкӧн ыджда.

32-ӧд серпас вылын вӧчӧма ∠AOB, кодӧс юкӧма 10 пельӧс градусӧ да вомӧналӧма AOB пельӧс йыв шӧрчута различнӧй радиуса кык дугаӧн. Серпасысь тыдалӧ, мый дугӧвӧй градусъяс абу ӧтыдждаӧсь да зависитӧны радиус кузьтаысь.

6 §. Пельӧсъяс вылын действийӧяс. Дорвыв пельӧсъяс.

1. Тӧдам кӧ пельӧсъяслысь градуснӧй мера, найӧс содтӧм да чинтӧм позьӧ вӧчны арталӧмӧн да построенньӧӧн.

1 задача. Корсьны пельӧсъяслысь сумма да разносьт: ∠ABC = 47°40’ да ∠DEF = 30°23’45’’.

Решитӧм. 1) 47°40’ + 30°23’45’’ = 78°3’45’’

2) 47°40’ − 30°23’45’’ = 17°16’15’’

Ӧтвет: 1) ∠ABC + ∠DEF = 78°3’45’’, 2) ∠ABC − ∠DEF = 17°16’15’’.

2 задача. Корсьны транспортирӧн вӧчӧмӧн ABC да DEF пельӧсъяслысь сумма; пельӧсъяслӧн ыджда сетӧма 35-ӧд серпас вылын.

Построенньӧ: Нуӧдам MN веськыд визь, сы вылын босьтам кутшӧмкӧ O чут, сійӧ O чутӧ транспортир отсӧгӧн вӧчам ∠NOK = ∠ABC; сэсся O чут бара босьтам кыдз мӧд пельӧслысь йыв да OK боксӧ кыдз сылысь ӧти бок да вӧчам ∠LOK = ∠DEF; сэк ∠LON — кык сетӧм пельӧсъяслӧн сумма:

∠ABC + ∠DEF = ∠NOK + ∠KOL = ∠LON.

3 задача. Корсьны транспортирӧн вӧчӧмӧн ABC да DEF пельӧсъяслысь разносьт; пельӧсъяслӧн ыджда сетӧма 36 серпас вылын.

Построенньӧ. Нуӧдам MN веськыд, сы вылын кутшӧмкӧ O чутӧ вӧчам ∠NOK = ∠ABC (36-ӧд серпас), сэсся сійӧ жӧ O чутӧ да MN веськыд вылӧ стрӧитам ∠NOL = ∠DEF, сэк ∠LOK — корсян разносьт:

∠LOK = ∠ABC − ∠DEF.

4 задача. ∠ABC ӧктыны 3 вылӧ.

Решитӧм. Задача пӧрӧ куим ӧтыджда пельӧс (сетӧм ABC пельӧс ыджда) водзысь-водзӧ содтӧмӧ.

2. Кык пельӧс, кодъяслӧн эм ӧтувъя йыв да ӧтувъя ӧти бок да кодъяс мӧда-мӧдсӧ оз вевттьыны, шусьӧны дорвыв пельӧсъясӧн.

35-ӧд серпас вылын ∠NOK да ∠KOL — дорвыв пельӧсъяс. ∠NOK да ∠NOL абу дорвыв пельӧсъяс.

3. Пельӧс пытшкӧсті кӧ нуӧдны веськыд визь, коді мед мунас йыв пыр, сійӧ веськыд визьӧн пельӧс юксяс кык дорвыв пельӧсӧ, кодъяс вермасны лоны ӧтыдждаӧсь либӧ оз.

Веськыд визь, коді юкӧ пельӧсӧс шӧри, шусьӧ ӧтыдждаӧ пельӧс юкысьӧн, либӧ пельӧс биссектрисаӧн.

Ӧтыджда да абу ӧтыджда пайясӧ пельӧс юкӧм лоӧ видлалӧма мӧдлаын.

7 §. Орчча пельӧсъяс, налӧн свойствояс. Теорема йылысь гӧгӧрвоӧм.

1. Кык дорвыв пельӧс: ∠AOC да ∠BOC (37-ӧд серпас), кодъяслӧн ӧти бок OC — ӧтувъя, а мӧд кык бок, OA да OB, мӧдара направленньӧаӧсь да вӧчӧны ӧти веськыд визь, шусьӧны орчча пельӧсъясӧн.

Босьтам вомӧнасян кык веськыд визь: AB да CD (38-ӧд серпас); найӧ вӧчӧны O чутын ӧтувъя йыла нёль пельӧс. Дорвыв пельӧсъяслӧн быд гоз: ∠AOC да ∠COB, ∠COB да ∠BOD да с. в. — орчча пельӧсъяс.

Орчча пельӧсъяс позьӧ вӧчны тадз: сетӧма ∠AOB (39-ӧд серп.); нюжӧдам сылысь кодсӧкӧ ӧти боксӧ, шуам OA, O йыв сайӧ, лоӧ выль пельӧс BOC, коді лоӧ сетӧм пельӧслы орчча, сы вӧсна, мый сыкӧд сылӧн эм ӧтувъя йыв — O, ӧтувъя бок — OB да сылӧн бок OC лоӧ AOB пельӧсса OA боклӧн нюжӧдӧм. ∠AOB да ∠BOC — орчча пельӧсъяс.

2. Эм-ӧ зависимосьт кык орчча пельӧс костын? Корсям сумма кык орчча пельӧсъяслысь: ∠AOB да ∠BOC-лысь.

∠AOB + ∠BOC = ∠AOC, а ∠AOC — павтыртӧм пельӧс, коді 2d ыджда, мӧд ног кӧ, кык веськыд пельӧс ыджда, сідзкӧ:

кык орчча пельӧслӧн сумма 2d ыджда.

Тайӧ кывъясӧн лои дженьыда шуӧма орчча пельӧсъяс свойство йылысь сужденньӧ.

3. Орчча пельӧсъяслӧн свойство йылысь выводӧ ми воим сэк, кор вӧчим некымын сужденньӧ, кодъясӧс лои подулалӧма тӧдса геометрическӧй фактъяс вылӧ.

Геометрическӧй фигураяслӧн свойствояс йылысь дженьыда висьталӧм сужденньӧ шусьӧ теоремаӧн; теоремалӧн справедливосьт лоӧ тыдалана сӧмын подулалӧм бӧрын — докажитӧм бӧрын, — тайӧс вӧчӧны тӧдса геометрическӧй фактъяс вылӧ ыстысьӧмӧн.

Дженьыда висьталӧм сужденньӧ “кык орчча пельӧс сумма 2d ыджда” лоӧ теорема.

Миянлы тӧдса нин сужденньӧ: “центральнӧй пельӧсъяс кӧ ӧтыдждаӧсь, налы соответствуйтысь дугаяс сідзжӧ ӧтыдждаӧсь” сідзжӧ лоӧ теорема.

Теоремаяскӧд ми паныдасявлім нин арифметикаын, кор сёрнитім лыдъяс свойствояс йылысь. Сужденньӧ: “лыд кӧ помасьӧ чётнӧй лыдпасӧн, сэк сійӧ юксьӧ 2 вылӧ” эм теорема.

4. Теоремаын торйӧдӧны: 1. Условийӧ, либӧ сійӧс, мый сетӧма. Сідз, теоремаын “кык орчча пельӧслӧн сумма 2d ыджда” сетӧма кык пельӧс: AOB да BOC; на йылысь тӧдам, мый найӧ орчча пельӧсъяс.

Условийӧ дженьыда гижан ног:

Сетӧма: ∠AOB да ∠BOC — орчча пельӧсъяс.

2. Вывод, либӧ сійӧ, мый колӧ докажитны. Сідз, теоремаын “кык орчча пельӧслӧн сумма 2d ыджда” колӧ докажитны, мый кык орчча пельӧслӧн сумма 2d ыджда.

Дженьыда гижӧд:

Колӧ докажитны: ∠AOB + ∠BOC = 2d.

Лӧсьыдджык теоремалысь условийӧ да сылысь вывод гижавны ӧти мӧд улӧ, кыдз мыччӧдӧма улынджык, — та дырйи условийӧсӧ выводысь юкӧны чертаӧн:

Сетӧма: ∠AOB да ∠BOC — орчча пельӧсъяс.

_______________________________________

Колӧ докажитны: ∠AOB + ∠BOC = 2d.

Теорема устанавливайтӧ геометрическӧй фигураяслысь определённӧй свойствояс. Теорема докажитігӧн ми пӧльзуйтчам различнӧй методъясӧн: 1) ӧти фигура мӧд вылӧ пуктан методӧн; 2) кык величина коймӧдкӧд ӧтыдждаалан методӧн; 3) паныдсянь докажитӧм методӧн; бӧръя докажитӧм мунӧ сідз, мый докажитанторсӧ лэдзам намӧдарӧ да сэсся сужденньӧяс вӧчӧмӧн воам сэтшӧм заключенньӧӧ, мый миян лӧсьӧдлӧмыс оз кут туйны.

Теорема “кык орчча пельӧслӧн сумма 2d ыджда” докажитӧма кык величина коймӧдкӧд ӧтыдждаалан методӧн. Збыльысь ӧд:

1) ∠AOB + ∠BOC = павтыртӧм пельӧс,

2) павтыртӧм пельӧс = 2d.

Тан кык величина 1) кык орчча пельӧслӧн сумма да 2) 2d — коймӧд величинакӧд — павтыртӧм пельӧскӧд — ӧтыдждаалӧма.

Медбӧрын, аксиомаӧн: “кык величина, кор найӧ торйӧн коймӧдкӧд ӧтыдждаӧсь, лоӧны мӧда-мӧдкӧд ӧтыдждаӧсь” пӧльзуйтчӧмӧн, петкӧдлам, мый

∠AOB + ∠BOC = 2d,

мӧд ног кӧ, кык орчча пельӧслӧн сумма 2d ыджда.

5. Сужденньӧяс, кодъяс веськыда петӧны аксиомаясысь да теоремаясысь, шусьӧны следствийӧясӧн.

Видзӧдлам следствийӧяссӧ татшӧм теоремаысь: “кык орчча пельӧслӧн сумма 2d ыджда”.

Следствийӧяс: 1) а) Сетӧм пельӧс кӧ ёсь, сылӧн орчча пельӧс тшӧтшыд, да мӧдарӧ.

b) Сетӧм пельӧс кӧ веськыд, сылӧн орчча пельӧс сідзжӧ веськыд.

Сідзкӧ,

c) Веськыд пельӧс эм кык ӧтыджда орчча пельӧс пиысь ӧтиыс.

2) Некымын дорвыв пельӧс кӧ куйлӧны сідз, мый первойя да медбӧръя пельӧсъяслӧн дорса бокъясыс мӧда-мӧдлы паныдаӧсь, мӧд ног кӧ, вӧчӧны ӧти веськыд визь, сэтшӧм пельӧсъяслӧн суммаыс 2d ыджда (40-ӧд серпас).

Тадзи и эм, став дорвыв пельӧсыс 40-ӧд серпас вылын артмӧдӧны павтыртӧм пельӧс, сідзкӧ налӧн суммаыс 2d ыджда.

3) Некымын дорвыв пельӧс кӧ куйлӧны сідз, мый первойя да медбӧръя пельӧсъяслӧн дорса бокъясыс вевсяасьӧны, сэтшӧм пельӧсъяслӧн суммаыс 4d ыджда (41-ӧд серпас).

Нюжӧдам O чут сайӧ кутшӧмкӧ пельӧслысь ӧти бок, шуам OA, лоӧ AA₁, коді ∠COD юкас кык юкӧнӧ.

Лоӧ:

∠AOE + ∠EOD + ∠DOA₁ = 2d

∠AOB + ∠BOC + ∠COA₁ = 2d

____________________________

Став пельӧсъяслӧн сумма = 4d.

6. а) Кык пельӧс, кодъяслӧн суммаыс 180° ыджда, либӧ 2d ыджда, шусьӧны пополнительнӧй пельӧсъясӧн; пополнительнӧй пельӧсъяс вылӧ пример: орчча пельӧсъяс.

b) Кык пельӧс, кодъяслӧн суммаыс 90° либӧ d ыджда, шусьӧны дополнительнӧй пельӧсъясӧн.

8 §. Перпендикуляр да пӧлыня визь.

1. Кык орчча пельӧсысь (42-ӧд серпас) ∠AOB < ∠BOE. Налысь кӧ ӧтувъя бок OB кутам бергӧдны O йыв гӧгӧр, OB вермас босьтны сэтшӧм положенньӧ OD, кор кыкнан орчча пельӧс лоӧны ӧтыдждаӧсь, мӧд ногӧн, кыкнаныс найӧ лоӧны веськыдӧсь. Татшӧм положенньӧ дырйи OD веськыд визь шусьӧ AE веськыдлы перпендикулярӧн, а O чутыс перпендикуляр подувтасӧн.

Тадз, веськыдлы перпендикулярӧн шусьӧ сэтшӧм веськыд визь, коді сыкӧд артмӧдӧ веськыд пельӧсъяс.

Кык веськыд визь AB да CD, кор найӧ вомӧнасигӧн артмӧны (43-ӧд серпас) веськыд пельӧсъяс, шусьӧны мӧда-мӧдлы перпендикулярнӧй веськыд визьясӧн.

Кык веськыдлӧн перпендикулярносьт пасйыссьӧ ⊥ пасӧн.

Гижӧд AB ⊥ CD лыддьысьӧ: AB лоӧ CD-лы перпендикуляр.

2. Перпендикуляр вӧчӧм вылӧ пӧльзуйтчӧны чертёжнӧй куимпельӧсаӧн, кодлӧн ӧти пельӧсыс веськыд, да линейкаӧн. Перпендикуляр нуӧдан способ мичаа тыдалӧ 44-ӧд серпас вылысь. BO₁ ⊥ CD.

3. OD веськыд визь AE веськыдлы перпендикуляр, OD ⊥ AE; тайӧ визьсьыс мукӧд став веськыд визьсӧ торйӧдӧм могысь, найӧс шуӧны пӧлыня визьясӧн, шуам OB (45-ӧд серпас), коді AE веськыдкӧд вӧчӧ тшӧтшыд либӧ ёсь пельӧс, а оз веськыдӧс; OB пӧлынялӧн AE веськыдкӧд вомӧнасянін O чут шусьӧ пӧлыня визь подувтасӧн.

4. Теорема. Веськыд визь вылын босьтӧм чут пыр позьӧ нуӧдны веськыдлы сӧмын ӧти перпендикуляр.

Сетӧма: OD ⊥ EA (46-ӧд серпас).

___________________________

Колӧ докажитны: OD лоӧ сӧмын дзик ӧти перпендикулярӧн EA-лы O чутын.

Докажитӧм. Шулам, мый EA-лы O чут пыр, OD перпендикулярысь ӧтдор, нуӧдӧма нӧшта перпендикуляр — OB; сэк OB перпендикуляр OA веськыдкӧд вӧчӧ веськыд пельӧс, а тайӧ лоӧ, мый ∠BOA ∠DOA ыджда сы вӧсна, мый веськыд пельӧсъяс ӧтыдждаӧсь; но ∠BOA лоӧ ∠DOA-лӧн сӧмын юкӧн, а юкӧн оз вермы лоны быдса ыджда; та серти ∠BOA оз вермы лоны ∠DOA ыджда; сідзкӧ, миян шулӧмным, мый EA-лы O чут пыр позьӧ OD-ысь ӧтдор нуӧдны нӧшта ӧти перпендикуляр, оз туй; татысь: OD веськыд сӧмын ӧтнас EA-кӧд вермӧ вӧчны веськыд пельӧс, а тайӧ лоӧ, мый веськыд визь вылын босьтӧм чут пыр позьӧ нуӧдны сылы сӧмын ӧти перпендикуляр.

9 §. Противоположнӧй пельӧсъяс.

1. AOB пельӧслысь кӧ кыкнан боксӧ нюжӧдны O йыв сайӧ (47-ӧд серпас), лоӧ ∠COD, кодлӧн сетӧм пельӧскӧд ӧтувъя O йыв. Кык пельӧс, AOB да COD, шусьӧны противоположнӧй пельӧсъясӧн сэк, кор ӧтиыслӧн бокъяс лоӧны мӧд пельӧсса бокъяслӧн нюжӧдӧм. Противоположнӧй пельӧсъяс артмӧны кык веськыд визь вомӧнасигӧн. Сэк O чут бердын лоӧ кык гоз противоположнӧй пельӧс: ∠AOB да ∠COD, ∠AOD да ∠BOC.

2. Теорема. Противоположнӧй пельӧсъяс ӧтыдждаӧсь.

Сетӧма: ∠AOB да ∠COD — противоположнӧй пельӧсъяс (47-ӧд серпас)

_____________________________________________________________

Колӧ докажитны: ∠AOB = ∠COD.

Докажитӧм. 1) ∠AOB + ∠BOC = 2d кыдз орччаяс,

2) ∠COD + ∠BOC = 2d кыдз орччаяс.

Сідзкӧ,

∠AOB + ∠BOC = ∠COD + ∠BOC,

та кузя

∠AOB = ∠COD.

Следствие. Кык веськыд визь вомӧнасигӧн артман нёль пельӧс пиысь ӧтилысь кӧ величина сетӧма, мукӧд куим пельӧслӧн величина тӧдмавсьӧ сетӧм пельӧс серти.

Юасянъяс да упражненньӧяс.

1. Ӧти чут гӧгӧр куйлысь кӧкъямыс дорвыв пельӧс пиысь мый ыджда быдӧн?

2. Ыджыд-ӧ быд пельӧс нёль пельӧс пиысь, кодъяс артмӧмаӧсь кык веськыд визь вомӧнасьӧмысь, на костын кӧ ӧти пельӧсыс 40° ыджда?4d/9 ыджда?

3. Вӧчны сетӧм ∠ABC-лы орчча пельӧс.

4. Кык орчча пельӧс относитчӧны кыдз 4 : 5. Тӧдмавны быд пельӧслысь ыдждасӧ.

5. Тӧдмавны пельӧс, коді ас орччасьыс 27°-ӧн ичӧтджык, 90°-ӧн ичӧтджык.

6. Ӧти чут гӧгӧр куйлӧны нёль дорвыв пельӧс; на пиын ӧти 0,6d, мӧд 20°, коймӧд 45°. Тӧдмавны нёльӧд пельӧс.

7. Тӧдмавны, кымын градус пельӧсын, коді 1) 5d/6, 2) 3d/8, 3) 1⅙d ыджда.

8. Тӧдмавны пельӧс кык веськыд визь костысь, кодъяс быд кык орчча пельӧсӧс юкӧны шӧри. Индыны, кыдзи мӧда-мӧд серти куйлӧны тайӧ веськыд визьясыс.

III. КУИМПЕЛЬӦСАЯС.

1 §. Веськыдвизя фигураяс.

1. Плоскосьтлӧн сэтшӧм юкӧныс, кодӧс ограничитӧма тупкӧса чегласьӧм визьӧн, шусьӧ унапельӧсаӧн. Чегласьӧм визьлӧн вундӧгъяс шусьӧны сійӧ бокъясӧн. Унапельӧсалӧн орчча быд кык бок вӧчӧны пельӧс. Унапельӧсаӧс нимтӧны пельӧс лыд серти, а оз бок лыд серти. Унапельӧсаын кымын пельӧс, сымын бок.

Плоскосьтлӧн юкӧн, кодӧс ограничитӧма куим вундӧга чегласьӧм визьӧн, шусьӧ куимпельӧсаӧн.

Плоскосьтлӧн юкӧн, кодӧс ограничитӧма нёль вундӧга чегласьӧм визьӧн, шусьӧ нёльпельӧсаӧн да с. в.

Плоскосьтлӧн юкӧн, кодӧс ограничитӧма n лыда вундӧга чегсьӧм визьӧн, шусьӧ n-пельӧсаӧн.

48-ӧд серпас вылын сетӧма куимпельӧсаӧс, нёльпельӧсаӧс, витпельӧсаӧс, квайтпельӧсаӧс.

2. Унапельӧса пасйыссьӧ латинскӧй алфавитса ыджыд шыпасъясӧн, кодъясӧс пукталӧны пельӧсъяс йывъяс бердӧ; унапельӧсаса пельӧсъяслӧн йывъяс шусьӧны сідзжӧ унапельӧсалӧн йывъяс. Кыв “куимпельӧса” гижигӧн вежӧны пасӧн ∆. Гижӧд ∆ABC лыддьыссьӧ: ABC куимпельӧса.

Куимпельӧсалысь бокъяс AB, BC да AC (49-ӧд серпас) пасйӧны сідзжӧ латинскӧй алфавитса ӧти ичӧт шыпасӧн, коді соответствуйтӧ куимпельӧсаса сійӧ пельӧссӧ пасйӧм вылӧ, код водзын куйлӧ бокыс. Сідз, AB бок, коді куйлӧ C водзын, пасйыссьӧ ичӧт c шыпасӧн, AC бок — ичӧт b шыпасӧн, BC бок — ичӧт a шыпасӧн.

Ичӧт шыпасӧн сідзжӧ пасйӧны боклысь кузьта, кодӧс мурталӧма кузьта мераяс определённӧй единицаясӧн. Сідз, пример вылӧ:

BC = a см, AC = b см, AB = c см.

Татшӧм пасйӧм серти лоӧ:

1) ∠A куйлӧ a бок водзын да b да c бокъяс костын;

2) ∠B куйлӧ b бок водзын да a да c бокъяс костын;

3) ∠C куйлӧ c бок водзын да a да b бокъяс костын.

Дзик жӧ сідз:

1) a дор бердӧ водӧны ∠B да ∠C;

2) b дор бердӧ водӧны ∠A да ∠C;

3) c дор бердӧ водӧны ∠A да ∠B.

3. Унапельӧса периметрӧн шусьӧ став боклӧн сумма.

∆ABC-лӧн периметр (49-ӧд серпас) сійӧ куим бок кузьтаяс сумма ыджда.

P = BC + CA + AB, либӧ P = a + b + c, кӧн P — периметр.

4. Веськыд визь, коді ӧтлаалӧ унапельӧсалысь кык йыв, кодъяс оз куйлыны ӧти бок вылын, шусьӧ диагональӧн.

Диагональяс унапельӧсаӧс торйӧдӧны куимпельӧсаясӧ. AC да AD диагональяс (50-ӧд серпас) ABCDE витпельӧсаӧс торйӧдӧны куим куимпельӧсаӧ: ABC, ACD да ADE.

5. Унапельӧсалысь свойствояс велӧдӧм вайӧдчӧ куимпельӧсалысь свойствояс велӧдӧмӧ, та вӧсна куимпельӧсаӧс велӧдӧмыд ёна коланатор.

2 §. Куимпельӧсаясӧс классификацияалӧм.

1. Бокъяс кузьта серти куимпельӧсаяс овлӧны: 1) разнӧй бока куимпельӧсаяс, 2) кык ӧткузя бока куимпельӧсаяс, 3) ӧткузя бокъяса куимпельӧсаяс (51-ӧд серпас).

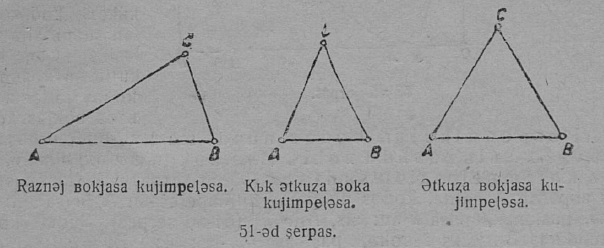
Разнӧй бока куимпельӧсаын бокъясыс разнӧй кузьтаӧсь; кык ӧткузя бока куимпельӧсаын кык бокыс ӧткузя; ӧткузя бокъяса куимпельӧсаын куимнан бокыс ӧткузяӧсь.

2. Пельӧсъяс величина серти куимпельӧсаяс овлӧны:

1) пӧлӧспельӧсаяс:

а) ёсьпельӧсаяс, кодъяслӧн став пельӧсыс ёсь;

b) тшӧтшыдпельӧсаяс, кодъяслӧн ӧти пельӧс тшӧтшыд;

2) веськыдпельӧсаяс, кодъяслӧн ӧти пельӧс веськыд (52-д сер.).

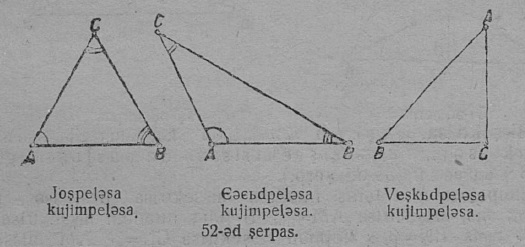
3. Веськыдпельӧса куимпельӧсалӧн бокъясыс торъя нимаӧсь: веськыд пельӧс йӧртысь бокъяс шусьӧны катетъясӧн, веськыд пельӧс водзын куйлысь бок шусьӧ гипотенузаӧн.

3 §. Куимпельӧсаын визьяс.

1. Судта. Куимпельӧсалысь кутшӧмкӧ ӧти бок босьтӧны подувтас пыдди. Подувтасӧн вермӧ лоны любӧй бок. Кор мунӧ сёрни куимпельӧсаса йыв йылысь, колӧ гӧгӧрвоны, мый сёрниыс мунӧ куим йыв письыс сійӧ йыв йылысь, коді куйлӧ подувтас водзын.

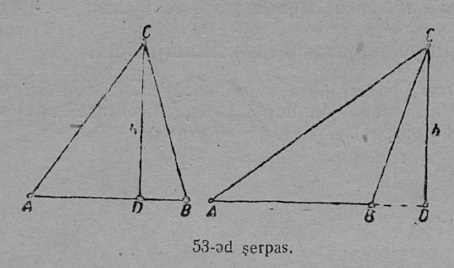
Кык ӧткузя бока куимпельӧсаын подувтасӧн босьтӧны сійӧ бок, коді абу ӧтыджда мукӧд кык боккӧд, а йылӧн шуӧны сійӧ пельӧслысь йывсӧ, коді куйлӧ сы водзын да кодӧс йӧртӧма ӧтыджда бокъяс костӧ.

Перпендикуляр, кодӧс нуӧдӧма куимпельӧсаыс йывсянь сылы паныда боклы либӧ бок нюжӧдӧмлы, шусьӧ куимпельӧсалӧн судтаӧн (53-ӧд серпас). Судта пасйӧны h шыпасӧн. h судта, кодӧс нуӧдӧма куимпельӧсаын A йывсянь a бокӧ, пасйӧны _a паса h-ӧн: сідз, AE = h_a (54-ӧд серпас). Судта, кодӧс нуӧдӧма B йылысь b бокӧ, пасйыссьӧ h_b-ӧн; сідз, BF = h_b; коймӧд судта CD = h_c.

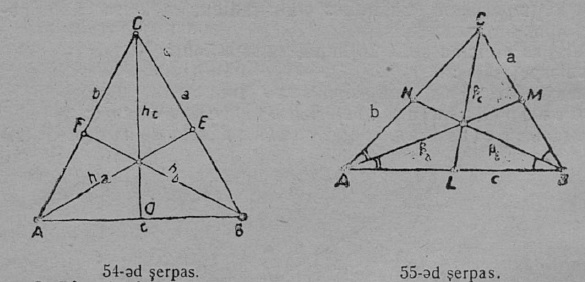
2. Биссектриса. Веськыд визь, коді куимпельӧсалысь пельӧс юкӧ шӧри, шусьӧ биссектрисаӧн да пасйыссьӧ греческӧй β шыпасӧн (55-ӧд серп.).

Куимпельӧсаын A йылысь нуӧдӧм биссектриса пасйыссьӧ _a паса β шыпасӧн; сідз, биссектриса AM = β_a. B йылысь нуӧдӧм биссектриса пасйыссьӧ β_b; сідз, BN = β_b; коймӧд биссектриса CL = β_c. AM биссектриса ∠A юкӧ шӧри, сідзкӧ,

∠CAM = ∠MAB = ½∠A.

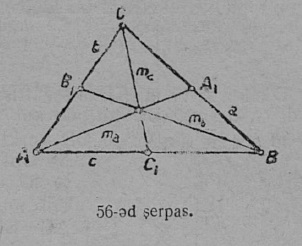
3. Медиана. AA₁ вундӧг (56-ӧд серпас), коді куимпельӧсаын A йыв ӧтлаалӧ сылы паныд куйлысь a бокса A₁ шӧркӧд, шусьӧ медианаӧн да пасйыссьӧ _a паса m-ӧн; сідз, AA₁ = m_a; медиана BB₁ = m_b; коймӧд медиана CC₁ = m_c.

AA₁ медиана BC = a бок юкӧ шӧри, сідзкӧ:

A₁B = A₁C = a/2.

57-ӧд серпас вылын ABC куимпельӧсаын нуӧдӧма CD судта, CE биссектриса да CF медиана. Судта, биссектриса да медиана куимпельӧсаын — куим различнӧй визьяс.

4 §. Куимпельӧсаын бокъяс костын соотношенньӧ.

57-ӧд серпас вылын сетӧма ∆ABC. A да B йывъяс — AB вундӧглӧн да ACB чегсьӧмлӧн помъяс.

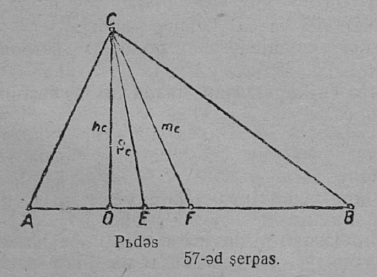
Веськыд визь йылысь аксиома серти AB вундӧг A да B чутъяс костын медся дженьыд расстоянньӧ, сідзкӧ, AB < AC + CB, кытысь

быд куимпельӧсаын сылӧн кык любӧй боклӧн сумма

коймӧд бокысь ыджыдджык.

AB < AC + CB неравенствоас кыкнан пайысь кӧ чинтыны ӧтыджда AC величина, лоӧ:

AB − AC < CB, либӧ CB > AB − AC, мӧд ног кӧ,

куимпельӧсаын быд бок кык мукӧд бокса разносьтысь ыджыдджык.

Сюрӧм вывод петкӧдлӧ, мый быдсяма куим вундӧг оз вермыны лоны куимпельӧса бокъясӧн; куим вундӧгысь позьӧ вӧчны куимпельӧсаӧс сӧмын сэк, кор любӧй кык вундӧглӧн сумма коймӧд вундӧгысь ыджыдджык.

5 §. Кык ӧткузя бока куимпельӧса. Сылӧн свойствояс.

Теорема. 1. Кык ӧткузя бока куимпельӧсаын йывса пельӧслӧн биссектриса ӧттшӧтш лоӧ медиана дай судта.

2. Кык ӧткузя бока куимпельӧсаын подувтас бердса пельӧсъяс ӧтыдждаӧсь.

Сетӧма:

∆ABC; 1) AC = CB;

2) CD — биссектриса; ∠1 = ∠2 = ∠C/2 (58-ӧд серпас).

____________________________________________

Колӧ докажитны:

1) CD — медиана, м. л. DA = DB,

2) CD — судта, м. л. CD ⊥ AB,

3) ∠A = ∠B.

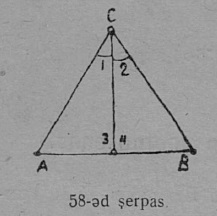
Докажитӧм. CD биссектрисаыс ∠C юкӧ кык ӧтыджда юкӧнӧ, 1 да 2, да ∆ABC торйӧдӧ кык куимпельӧсаӧ: ∆ACD да ∆CBD. 58-ӧд серпас кусыньтам CD веськыд кузя да петкӧдам, мый ACD да CBD куимпельӧсаяс вевсяасясны. Тайӧ сідзи и лоӧ, ∠1 да ∠2 равенство серти CA бок мунас CB бок вывті; сы вӧсна, мый AC = CB, A чут усьӧ B чутӧ; сы вӧсна, мый D чут коли важ инӧ, а A да B чутъяс ӧтлаасисны, DA да DB бокъяс сідзжӧ вевсяасясны; сідзжӧ та дырйи вевсяасясны ∠3 да ∠4, ∠A да ∠B. ACD да CBD куимпельӧсаясса став элементъяснаныс ӧтвесьтаасьӧмысь петӧ, мый:

1) DA = DB, а тайӧ лоӧ, мый D — AB подувтаслӧн шӧр да CD вундӧг лоӧ медиана;

2) ∠3 = ∠4; сы вӧсна, мый тайӧ пельӧсъяс, кыдз орчча да мӧда-мӧдкӧд ӧтыдждаӧсь, веськыдӧсь, CD ⊥ AB да CD вундӧг — судта;

3) ∠A = ∠B, — кык ӧткузя дора куимпельӧсаын подувтас бердса пельӧсъяс ӧтыдждаӧсь. Теорема лои докажитӧма.

Следствийӧяс. 1. Ӧти сійӧ жӧ куимпельӧсаын ӧтыджда бокъяс весьтын ӧтыджда пельӧсъяс.

∆ABC-ын кӧ кык бок ӧтыдждаӧсь, AC = CB, сэк сійӧ — кык ӧткузя бока куимпельӧса, а сэн ӧтыджда бокъяс водзын пельӧсъяс ӧтыдждаӧсь, л. м. ∠A = ∠B.

2. Кык ӧткузя бока куимпельӧсаын йывсянь подувтасӧ нуӧдӧм перпендикуляр юкӧ шӧри 1) подувтас да 2) йывса пельӧс.

3. Кык ӧткузя бока куимпельӧсаын подувтас шӧр куимпельӧсаса йывкӧд ӧтлаалысь вундӧг лоӧ вундӧглы^колӧ гижны “подувтаслы” — А. В./^ перпендикуляр да да юкӧ шӧри йывса пельӧс.

4. Кык ӧткузя бока куимпельӧсаын подувтаслы перпендикуляр, кодӧс нуӧдӧма сійӧ шӧр пыр, мунӧ куимпельӧсаыс йыв пыр да юкӧ йывса пельӧссӧ шӧри.

6 §. Осевӧй симметрия.

1. Симметричнӧй чутъяс. Босьтам веськыд MN визь, кытчӧкӧ сысянь шуйгавылӧ пуктам A чут, сэсся серпас кусыньтам MN веськыд кузя сідз, мед шуйгавыв юкӧн вевттяс веськыд вывсӧ. Сэк A чут усьӧ A₁ чутӧ (59-ӧд серпас). Татшӧм кык чут йылысь шуӧны, мый найӧ MN веськыд серти куйлӧны симметричнӧя, MN веськыд визьсӧ шуӧны симметрия осьӧн.

Мед тӧдмавны, кутшӧм свойствояс эмӧсь A да A₁ симметричнӧй чутъяслӧн, ӧтлаалам найӧс AA₁ веськыдӧн, коді симметриялысь MN ось вомӧналас B чутын.

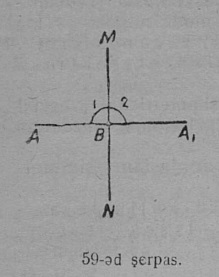
MN ось кузя серпас (59-ӧд серпас) кусыньтігӧн A чут усьӧ A₁ чутӧ да ∠1 да ∠2 ӧтлаасясны, сідзкӧ:

1) ∠1 = ∠2, тайӧ пельӧсъяс орччаӧсь; сы вӧсна, мый найӧ ӧтыдждаӧсь, ∠1 да ∠2 — веськыд пельӧсъяс, сідзкӧ, MN ⊥ AA₁, м. л. MN симметрия осьыс — AA₁ вундӧглы, коді ӧтлаалӧ симметричнӧй A да A₁ чутъяс, перпендикуляр.

2) BA = BA₁, сідзкӧ, B чут AA₁ вундӧглӧн шӧр да A да A₁ чутъяс MN симметрия осьсянь ӧтылнаынӧсь.

Сідзкӧ: 1) ось серти симметричнӧй чутъяс куйлӧны симметрия осьлы перпендикуляр вылын, осьсяньыс ӧтылнаын да ӧтарын и мӧдарын, либӧ: 2) кык чутлӧн симметрия осьыс — перпендикуляр найӧс ӧтлаалысь вундӧглы да мунӧ сы шӧр пыр.

Задача. Сетӧма A, B да C чутъяс да ось — MN; тэчны чутъяс, мед найӧ вӧліны MN ось серти A, B да C чутъяслы симметричнӧйӧсь.

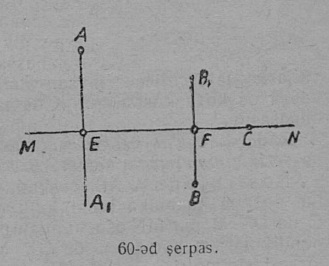
Построенньӧ. A да B чутъясысь (60-ӧд серпас) нуӧдам MN веськыдлы перпендикуляръяс да найӧс нюжӧдӧм вылӧ пукталам вундӧгъяс: EA₁ = AE да FB₁ = BF; лоӧны A₁ да B₁ чутъяс, кодъяс A да B-кӧд симметричнӧйӧсь. C чутлы, коді куйлӧ симметрия ось вылын, ачыс C чут лоӧ аслыс симметричнӧй.

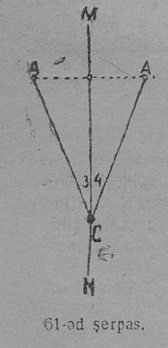
2. Симметричнӧй веськыдъяс. A да A₁ чутъясыс — MN ось серти симметричнӧй чутъяс (61-ӧд серпас). Симметрия MN ось вылын кӧ кӧнкӧ босьтны C чут да ӧтлаавны сійӧс A да A₁ симметричнӧй чутъяскӧд, артмасны CA да CA₁ веськыдъяс, кодъяс MN ось кузя серпассӧ кусыньтігӧн ӧтлаасясны. Татшӧм веськыдъяс шусьӧны симметричнӧй веськыдъясӧн. 61-ӧд серпасӧс MN ось кузя кусыньтӧмысь аддзам, мый тшӧтш ӧтлаасясны ∠3 да ∠4 , кодъясӧс артмӧдӧны оськӧд симметричнӧй CA да CA₁ веськыдъяс, сідзкӧ, ∠3 = ∠4; тайӧ лоӧ, мый кык симметричнӧй CA да CA₁ веськыдъяслӧн симметрия MN ось юкӧ наӧн артмӧдӧм пельӧссӧ шӧри, мӧд ногӧн, ось лоӧ тайӧ пельӧслӧн биссектриса. Сідзкӧ, кык вомӧнасян симметричнӧй веськыдъясӧн артман пельӧслӧн биссектриса лоӧ налӧн симметрия осьӧн.

Кык вомӧнасян симметричнӧй веськыд визьяслӧн симметрия ось йылысь тайӧ сужденньӧ позьӧ шуны тадз:

биссектриса — пельӧс бокъяслӧн симметрия ось.

Кык ӧткузя бока куимпельӧсаын йывса пельӧслӧн биссектрисаыс — куимпельӧсаса бокъяслӧн симметрия ось.

Кык ӧткузя бока ABC куимпельӧсаын йыв бердас C пельӧсса CD биссектриса вылын босьтӧм любӧй чут пыр кӧ нуӧдны биссектрисалы перпендикуляр, сійӧ CA да CB бокъяскӧд вомӧнасяс кык симметричнӧй K да L чутъясын; тайӧ чутъясыс йывсянь ӧтылнаынӧсь — сы вӧсна, мый 62 серпас вывса ось кузя кусыньтігӧн K да L чутъяс да CK да CL вундӧгъяс ӧтлаасясны.

Задача. Вӧчны веськыд визь, мед сійӧ вӧлі сетӧм симметрия MN ось серти симметричнӧй сетӧм AB веськыдлы (63-ӧд серпас).

Построенньӧ. AB веськыд вылын босьтам кутшӧмкӧ любӧй кык чут: C да D. На пыр MN осьлы нуӧдам перпендикуляръяс, корсям C да D чутъяскӧд симметричнӧй чутъяс C₁ да D₁. Тайӧ чутъяс пыр нуӧдам веськыд A₁B₁ визь, коді лоӧ сетӧм AB веськыдкӧд симметричнӧй.

3. Симметричнӧй фигураяс. Кык фигура шусьӧны ось серти симметричнӧйясӧн, кор ӧти фигураса быд чутлы соответствуйтӧ мӧд фигура вылын симметричнӧй чут.

Фигура шусьӧ симметричнӧйӧн, кор сы пытшкӧсті позьӧ нуӧдны сэтшӧм веськыд, мый сы кузя кусыньтігӧн фигуралӧн ӧти юкӧн стӧч вевсяасяс мӧд юкӧнкӧд. Кык ӧткузя дора куимпельӧса — симметричнӧй фигура (62-ӧд серпас); сылӧн судта, коді сійӧ жӧ кадӧ лоӧ йывса пельӧслы биссектрисаӧн, — сылӧн симметрия ось.

Кытшвизь — симметричнӧй фигура, любӧй диаметр сылӧн — симметрия ось.

Юасянъяс да упражненньӧяс:

1. Мый вӧсна ӧткузя бокъяса куимпельӧсаын сылӧн любӧй судта ӧттшӧтш биссектриса дай медиана?

2. Кутшӧм визь кругын лоӧ симметрия осьӧн диаметрлы?

3. Медиана, кодӧс нуӧдӧма кык ӧткузя бока куимпельӧсаын боквывса бокӧ, юкӧ сылысь периметр 7,5 см. да 6,5 см. ыджда юкӧнъясӧ. Тӧдмавны бокъяссӧ.

4. Вӧчны веськыдпельӧса куимпельӧса, мед сійӧ вӧлі симметричнӧй сетӧмлы, симметрия осьсӧ татшӧмӧс босьтӧмӧн: а) кутшӧмкӧ ӧти катет, b) гипотенуза. Индыны, кутшӧм фигура артмас, кор симметрия ось пыдди лоӧ босьтӧма катет.

5. Докажитны, мый кык вомӧнасян веськыд визьяслӧн симметрия осьяс мӧда-мӧдлы перпендикулярнӧйӧсь.

IV. КУИМПЕЛЬӦСАЯСЛӦН РАВЕНСТВО.

1 §. Куимпельӧсаяс равенство йылысь куим признак.

Кык фигура мӧда-мӧдкӧд равнӧйӧсь сэк, кор ӧтисӧ мӧдыс вылӧ пуктігӧн найӧ став элементъяснаныс — бокъяснас да пельӧсъяснас — вевсяасьӧны.

1. Первойя признак.

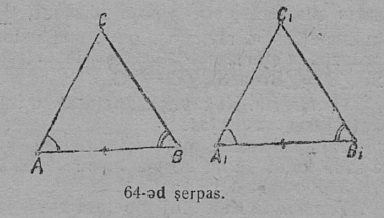
Теорема. Кык куимпельӧса равнӧйӧсь, кор ӧти куимпельӧсалӧн ӧти бок да сы бердса кык пельӧс мӧд куимпельӧсаса боккӧд да сы бердса кык пельӧскӧд ӧтыдждаӧсь.

Сетӧма:

∆ABC да ∆A₁B₁C₁; 1) A₁B₁ = AB; 2) ∠A₁ = ∠A;

3) ∠B₁ = ∠B (64-ӧд серпас)

____________________________________

Колӧ докажитны: ∆A₁B₁C₁ = ∆ABC.

Докажитӧм. Пуктам ∆A₁B₁C₁ ∆ABC вылӧ сідз, мед A₁ йыв усьӧ A йылӧ да A₁B₁ бок мунас AB бок кузя; сэк сы вӧсна, мый A₁B₁ да AB ӧтыдждаӧсь, B₁ чут усьӧ B чутӧ, а сы вӧсна, мый ∠A₁ = ∠A да ∠B₁ = ∠B, A₁C₁ бок мунас AC бок кузя да B₁C₁ бок — BC бок кузя. Коймӧд йыв C₁ усьӧ C чутӧ сы вӧсна, мый C да C₁ чутъяс определяйтчӧны ӧти сійӧ жӧ ӧтлаасьӧм веськыд визьяс вомӧнасьӧмӧн. Тадз, ∆A₁B₁C₁ да ∆ABC вевсяасисны; сідзкӧ найӧ равнӧйӧсь, ∆A₁B₁C₁ = ∆ABC. Сыысь, мый куимпельӧсаяс равнӧйӧсь, петӧ, мый налӧн равнӧйӧсь соответственнӧ расположеннӧй элементъяс: A₁C₁ = AC; B₁C₁ = BC; ∠C₁ = ∠C.

Следствийӧ. Кык веськыдпельӧса куимпельӧса равнӧйӧсь сэк, кор налӧн соответственнӧй катетъяс да найӧ бердса ёсь пельӧсъяс ӧтыдждаӧсь.

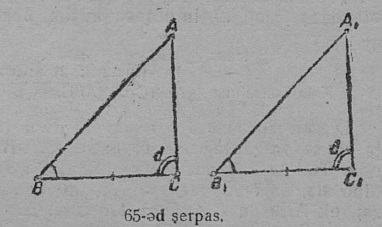
Кык веськыдпельӧса куимпельӧса ABC да A₁B₁C₁ (65-ӧд серпас) равнӧйӧсь: налӧн соответственнӧй катетъяс равнӧйӧсь, шуам, B₁C₁ = BC, да сійӧ катетъяс бердын эмӧсь кык ӧтыджда пельӧс: ∠B₁ = ∠B условийӧ серти да ∠C₁ = ∠C кыдз веськыд пельӧсъяс.

2. Мӧд признак.

Теорема. Кык куимпельӧса равнӧйӧсь, кор ӧти куимпельӧсалӧн кык бок да на костӧ йӧртӧм пельӧс мӧд куимпельӧсаса кык боккӧд да на костӧ йӧртӧм пельӧскӧд ӧтыдждаӧсь.

Сетӧма:

∆ABC да ∆A₁B₁C₁. 1) A₁B₁ = AB; 2) A₁C₁ = AC да

3) ∠A₁ = ∠A (66-ӧд серпас).

_________________________________________

Колӧ докажитны: ∆A₁B₁C₁ = ∆ABC.

Докажитӧм. ∆A₁B₁C₁ вевсяӧдам ∆ABC вылӧ сідз, мед A₁ йыв усьӧ A йылӧ да A₁B₁ бок мунас AB бок кузя; сэк A₁B₁ да AB ӧтыджда серти B₁ чут усьӧ B чутӧ; A да A₁ пельӧсъяс ӧтыджда серти A₁C₁ бок мунас AC бок кузя; сы вӧсна, мый A₁C₁ = AC, C₁ чут усьӧ C чутӧ; такӧд ӧттшӧтш ӧтлаасясны C₁B₁ да CB сы вӧсна, мый налӧн помса чутъяс C₁ да C, B₁ да B ӧтлаасисны. A₁B₁C₁ да ABC куимпельӧсаяс ӧтлаасисны, сідзкӧ найӧ ӧтыдждаӧсь, ∆A₁B₁C₁ = ∆ABC. Сыысь, мый куимпельӧсаяс равнӧйӧсь, петӧ, мый налӧн став соответственнӧя расположитӧм элементъяс — бокъяс да пельӧсъяс — ӧтыдждаӧсь: 1) C₁B₁ = CB; 2) ∠B₁ = ∠B да 3) ∠C₁ = ∠C.

Следствийӧ. Кык веськыдпельӧса куимпельӧса равнӧйӧсь, кор налӧн катетъясыс равнӧйӧсь.

Тайӧ сы вӧсна, мый веськыдпельӧса куимпельӧсаяслӧн эмӧсь кык ӧтыджда катет да на костса ӧтыджда веськыд пельӧс.

3. Коймӧд признак.

Теорема. Кык куимпельӧса равнӧйӧсь, кор ӧтиыслӧн куим бок ӧтыдждаӧсь мӧд куимпельӧса куим боккӧд.

Сетӧма:

∆ABC да ∆A₁B₁C₁.

1) A₁B₁ = AB; 2) A₁C₁ = AC; 3) B₁C₁ = BC (67-ӧд серпас).

______________________________________

Колӧ докажитны: ∆A₁B₁C₁ = ∆ABC.

Докажитӧм. Бергӧдам ∆A₁B₁C₁ 180° вылӧ A₁B₁ бок гӧгӧр, тайӧ боксӧ вӧрзьӧдтӧг кольӧмӧн; сэк ∆A₁B₁C₁ воас ∆A₁B₁C₂ положенньӧӧ. Тыдалӧ, мый ∆A₁B₁C₁ = ∆A₁B₁C₂. Сэсся ∆A₁B₁C₂ пуктам ∆ABC дінӧ сідз, мед A₁ чут усьӧ A чутӧ да A₁B₁ бок мунас AB бок кузя; сэк A₁B₁ да AB равенство серти B₁ чут усьӧ B чутӧ да C₂ йыв босьтас C₃ положенньӧ. Ӧтлаалам сэсся CC₃ веськыдӧн C йыв C₃ йывкӧд; пасъям пельӧсъяс, кодъясӧ CC₃ веськыд торйӧдіс C да C₃ пельӧсъяс, соответственнӧя 1, 2, 3 да 4-ӧн да видзӧдлам артмӧм кык ӧткузя бока куимпельӧсаяс: ACC₃ да CBC₃, кодъяслӧн CC₃ ӧтувъя подувтас, AC = AC₃ да BC = BC₃.

Кык ӧткузя бока куимпельӧсаясын подувтас бердса пельӧсъяс равнӧйӧсь, та вӧсна:

1) ∆ACC₃-ын ∠1 = ∠3.

2) ∆CBC₃-ын ∠2 = ∠4.

Содтам членӧн-членӧн да лоӧ:

∠1 + ∠2 = ∠3 + ∠4,

но

∠1 + ∠2 = ∠C да ∠ 3 + ∠ 4 = ∠C₃,

та вӧсна ∠C = ∠C₃.

Ӧні видзӧдлам ∆ABC да ∆ABC₃: налӧн AC = AC₃, BC = BC₃ да докажитӧм серти ∠C = ∠C₃; сідзкӧ тайӧ куимпельӧсаяс равнӧйӧсь, ∆ABC = ∆ABC₃, кык бок да на костса пельӧс серти; но ∆ABC₃ = ∆A₁B₁C₂ = ∆A₁B₁C₁ да ∆ABC₃ = ∆ABC, та вӧсна ∆A₁B₁C₁ = ∆ABC. Теорема лои докажитӧма.

2 §. Построенньӧ вылӧ основнӧй задачаяс.

Куимпельӧсаяс равенство йылысь теоремаяс серти позьӧ решитны линейка да циркуль отсӧгӧн уна задача построенньӧ вылӧ да сетны докажитӧм, мый вӧчӧм построенньӧыс дзик веськыд (правильнӧй).

1 задача. Вӧчны куимпельӧса, мед сійӧ вӧлі сетӧм ABC куимпельӧсакӧд ӧтыджда (68-ӧд серпас).

Построенньӧ. MN произвольнӧй веськыд вылӧ пуктам вундӧг: A₁B₁ = AB, ∆ABC-са бок ыдждаӧс; A₁ да B₁ чутъяс босьтам шӧрчутъяс пыдди, гижтам ∆ABC-са AC да BC бокъяс ыджда радиусъясӧн дугаяс; налысь вомӧнасян чут C₁ ӧтлаалам A₁ да B₁ чутъяскӧд; артмас корсян куимпельӧса: ∆A₁B₁C₁.

Збыльысь, ∆A₁B₁C₁ = ∆ABC сы вӧсна, мый налӧн A₁B₁ = AB, A₁C₁ = AC да B₁C₁ = BC.

2 задача. Вӧчны куимпельӧсаӧс сетӧм куим бок серти: a, b да c.

Куимпельӧсаӧс позьӧ вӧчны сэк сӧмын, кор сетӧм куим вундӧгысь быд ӧтиыс ичӧтджык мӧд кык суммаысь, шуам, a < b + c. Тайӧ условийӧ колӧ прӧверитны сӧмын медыджыд вундӧг йылысь сы вӧсна, мый ичӧтджык вундӧгъяс костысь быд вундӧг лоӧ мукӧд кык вундӧг суммаысь нӧшта нин ичӧтджык.

Медводз прӧверитам, соблюдайтчӧ-ӧ индӧм условийӧыс сетӧм вундӧгъяс дырйи; соблюдайтчӧ кӧ, кутам вӧчны.

Построенньӧ вӧчсьӧ воддза задачаын индӧм приёмӧн.

Задачаса сетӧмъяс (даннӧйяс) серти позьӧ вӧчны мыйта колӧ куимпельӧсаяс, но найӧ ставныс мӧда-мӧд вылӧ пуктігӧн кутасны ӧтлаасьны. Сідзкӧ, задача сетӧмъяс серти позьӧ вӧчны сетӧм формаа да сетӧм размера сӧмын ӧти куимпельӧсаӧс.

3 задача. Вӧчны пельӧс, мед сійӧ вӧлі сетӧм ыджда.

Построенньӧ. Сетӧма ∠ABC (69-ӧд серпас). Нуӧдам MN веськыд да сы вылын кӧнкӧ пасъям D чут. Нуӧдам произвольнӧй, но ӧткузя радиусӧн кык дуга, ӧтиӧс B йылын шӧрчутӧн, коді ABC пельӧслысь бокъяссӧ вомӧналӧ K да L чутъясын, а мӧдӧс — D чутын шӧрчутӧн. Тайӧ дугаыслӧн MN веськыдкӧд вомӧнасян E чутысь нуӧдам LK хорда ыджда радиусӧн дуга; тайӧ дуга воддза дугакӧд вомӧнасяс F чутын; F чут D чуткӧд ӧтлаалӧм бӧрын артмас корсян пельӧс ∠EDF = ∠ABC.

Медым докажитны, мый татшӧм построенньӧӧн артмӧм ∠EDF = ∠ABC, ӧтлаалам веськыд визьӧн E да F чутъяс да видзӧдлам DEF да BKL куимпельӧсаяс. ∆DEF = ∆BKL сы вӧсна, мый налӧн DE = BL, DF = BK да EF = KL построенньӧ серти, кыдз ӧтыджда кытшвизьяслӧн радиусъяс.

Куимпельӧсаяс равенствоысь петӧ, мый ∠EDF = ∠BKL кыдз ӧтыджда куимпельӧсаясса ӧтыджда FE да LK бокъяс водзын куйлысь пельӧсъяс. Сідзкӧ,

∠EDF = ∠LBK = ∠ABC.

4 задача. Вӧчны куимпельӧсаӧс b да c кык бок да найӧ костӧ йӧртӧм A пельӧс серти.

Построенньӧ. MN произвольнӧй веськыд визь вылӧ кутшӧмкӧ A чутсянь пуктам вундӧг: AB = c да A чут бердӧ вӧчам сетӧм A пельӧс ыджда пельӧс, сідзикӧн, мед сылӧн ӧти бок мунас MN веськыд кузя; пельӧсса мӧд бок кузя пуктам вундӧг: AC = b; C чут ӧтлаалам B чуткӧд, артмас ABC куимпельӧса, коді кутас удовлетворяйтны задачаса условийӧяслы.

5 задача. Вӧчны куимпельӧсаӧс c бок да сы бердса A да B кык пельӧс серти.

Построенньӧ. MN произвольнӧй веськыд визь вылӧ кутшӧмкӧ A чутсянь пуктам вундӧг: AB = c; A чут бердӧ вӧчам сетӧм A пельӧс ыджда пельӧс да B чут бердӧ — сетӧм B пельӧс ыджда пельӧс сідз, мед AB вундӧг налы вӧлі ӧтувъя бокӧн; сэк мӧд кык бокъяс A да B пельӧсъяслӧн вомӧнасясны C чутын, код лоӧ ABC корсян куимпельӧсалӧн коймӧд йыв. Кык веськыд визьяс вермӧны вомӧнасьны сӧмын ӧти чутын, та вӧсна сетӧм задача условийӧяс серти вермӧ лоны сӧмын ӧти решенньӧ: построенньӧ артмӧдӧ ӧти определённӧй формаа да ӧти определённӧй размера куимпельӧса.

6 задача. Сетӧм пельӧс юкны шӧрипӧв.

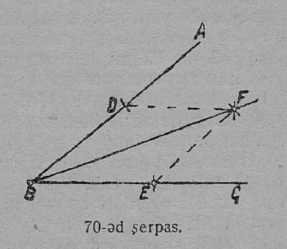
Построенньӧ. Сетӧма ∠ABC (70-ӧд серпас). Нуӧдам произвольнӧй радиусӧн B йылын шӧрчута дуга, коді пельӧслысь бокъяс вомӧналас D да E чутъясын.

Ӧтыджда радиусъясӧн нуӧдам D да E чутъясын шӧрчута кык дуга сідз, мед найӧ вомӧнасясны. Артмас F чут, кодӧс ӧтлаалам B йывкӧд. BF лоӧ сетӧм ABC пельӧслӧн биссектриса.

Докажитӧм. F чут ӧтлаалам D да E чутъяскӧд; лоӧ кык куимпельӧса: ∆BDF да ∆BEF; найӧ ӧтыдждаӧсь сы вӧсна, мый налӧн: 1) BF — ӧтувъя бок, 2) BE = BD, кыдз ӧтыджда кругкытшъяслӧн радиусъяс.^колӧ содтыны: EF = DF. — А. В. /^ Та вӧсна ∠FBE = ∠FBD, кыдз ӧтыджда куимпельӧсаясын ӧтыджда EF да FD бокъяс водзын куйлысь пельӧсъяс.

Сідзкӧ, BF веськыд юкӧ ∠ABC шӧри; BF — пельӧслӧн биссектриса.

Юкам кӧ FBD да FBE пельӧсъясӧс быдӧнӧс шӧри, сетӧм пельӧс юксяс ӧтыджда нёль юкӧнӧ. Татшӧм жӧ построенньӧӧн быд артмӧм пельӧс шӧри юкӧмӧн позьӧ сетӧм пельӧс юкны 8, 16 да с. в. ӧтыджда юкӧнӧ, либӧ вообще 2n ӧтыджда юкӧнӧ.

7 задача. Нуӧдны перпендикуляр веськыд визьлы сы вылын сетӧм чут пыр.

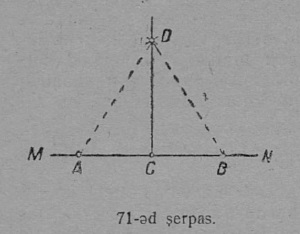
Построенньӧ. MN веськыд вылын сетӧм C чутсянь ӧтарӧ и мӧдарӧ пуктам произвольнӧй кузя CA да CB вундӧгъяс^ӧтыджда вундӧгъяс. — А. В./^ (71-ӧд серпас); нуӧдам произвольнӧй, но AC-ысь ыджыдджык радиусӧн, A да B чутъясын шӧрчута дугаяс^ӧтыджда дугаяс. — А. В./^ сідз, мед найӧ вомӧнасисны. Дугаяс вомӧнасян D чут ӧтлаалам C чуткӧд; CD веськыд — корсян перпендикуляр.

Докажитӧм. D чутӧс A да B чутъяскӧд ӧтлаалӧм бӧрын артмасны DCA да DCB куимпельӧсаяс; найӧ равнӧйӧсь сы вӧсна, мый налӧн 1) DC — ӧтувъя бок, 2) CA = CB построенньӧ серти, 3) AD = BD, кыдз ӧтыджда кытшвизьяслӧн радиусъяс. Та серти ∠DCA = ∠DCB; тайӧ пельӧсъяс орччаӧсь да ӧтыдждаӧсь, та вӧсна найӧ кыкнаныс веськыдӧсь. Татысь CD ⊥ AB, либӧ CD ⊥ MN. Тадз лои, мый CD — корсян перпендикуляр.

8 задача. Нуӧдны перпендикуляр сетӧм MN веськыдлы A чут пыр, кодӧс сетӧма веськыд визь сайын (72-ӧд серпас).

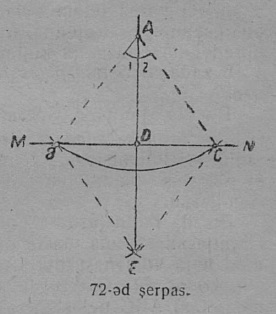
Построенньӧ. Нуӧдам сетӧм A чутын шӧрчута дуга сідз, мед сійӧ сетӧм MN веськыдкӧд вомӧнасяс B да C чутъясын. Нуӧдам ӧтыджда радиусъясӧн B да C чутъясын шӧрчута дугаяс, кодъяс вомӧнасясны кутшӧмкӧ E чутын, коді лоӧ A-сянь MN мӧдарын. A да E чутъяс ӧтлаалам да лоӧ корсян AE перпендикуляр.

Докажитӧм. A да E чутъясӧс B да C чутъяскӧд ӧтлаалӧм бӧрын лоӧ, мый ∆ABE = ∆ACE сы вӧсна, мый налӧн: 1) AE — ӧтувъя бок, 2) AB = AC, кыдз ӧти сійӧ жӧ дугалӧн радиусъяс, 3) BE = CE, кыдз ӧтыджда кытшвизьяслӧн радиусъяс. Куимпельӧсаяс равенствоысь петӧ, мый ∠1 = ∠2. Видзӧдлам ∆ABC; сійӧ — кык ӧткузя бока: сылӧн AB = AC да AD лоӧ ∠A-лӧн биссектриса сы вӧсна, мый ∠1 = ∠2. Кык ӧткузя бока куимпельӧсаын йывса пельӧслӧн биссектриса ӧттшӧтш сылӧн судта, та кузя AD ⊥ BC, либӧ AD ⊥ MN.

9 задача. Сетӧм вундӧг юкны шӧрипӧв.

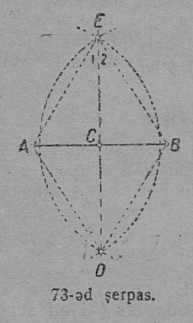
Построенньӧ. Нуӧдам произвольнӧй радиусӧн, но AB вундӧг джынысь ыджыдджыкӧн, сетӧм AB вундӧг A да B помъясын шӧрчутъяса дугаяс сідз, мед найӧ вомӧнасясны AB вундӧг ортсын ӧтарын и мӧдарын (73-ӧд серпас). Дугаяс вомӧнасян E да D чутъяс ӧтлаалысь веськыд ED вомӧналас AB вундӧгӧс C чутын, коді лоӧ сетӧм AB вундӧглӧн шӧр.

Докажитӧм. D да E чутъясӧс A да B чутъяскӧд ӧтлаалӧм бӧрын лоӧ некымын куимпельӧса. Равнӧй ADE да DBE куимпельӧсаясысь петӧ, мый ∠1 = ∠2; кык ӧткузя бока ABE куимпельӧсаысь, кодлӧн ∠1 = ∠2, петӧ, мый EC — йывса E пельӧслӧн биссектриса да ӧттшӧтш AB боклӧн медиана, та вӧсна CA = CB, либӧ C чут AB вундӧглӧн шӧр.

Юасянъяс да упражненньӧяс:

1. Кымын да кутшӧм условийӧясӧн определяйтчӧ ӧткузя бока куимпельӧсаяслӧн равенство?

2. Мый вӧсна кык ӧткузя бока куимпельӧсаяслысь равенство установитӧм вылӧ тырмымӧн тӧдны сӧмын, ӧтыдждаӧсь-ӧ наын: 1) йылын пельӧс да боквывса бок, 2) подувтас да сы бердын пельӧс, 3) подувтас да боквывса бок?

3. Кык ӧткузя бока ABC куимпельӧсаын подувтас бердса A да B пельӧсъяс йывъяссянь нуӧдӧма AM да BN медианаяс. Докажитны, мый медианаяс ӧтыдждаӧсь: AM = BN.

Гижны: 1) Кутшӧм соответственнӧй ӧтыджда элементъяс сетӧма, 2) кутшӧм кык куимпельӧсалысь равенство колӧ докажитны.

4. Докажитны, мый кык ӧткузя бока куимпельӧсаын подувтас бердса пельӧсъяслӧн биссектрисаяс ӧтыдждаӧсь.

5. Ӧтыджда ABC да A₁B₁C₁ куимпельӧсаясӧс пуктӧма мӧда-мӧд дінӧ найӧ бокъясӧн: AB = A₁B₁. Докажитны, мый CC₁ веськыд, коді ӧтлаалӧ налысь C да C₁ йывъяс, лоӧ найӧ ӧтувъя AB боклы перпендикуляр: CC₁ ⊥ AB.

6. Вӧчны куимпельӧса a да b кык бок да h_a судта серти.

7. Вӧчны куимпельӧса a да c кык бок да m_b медиана серти.

8. Вӧчны кык ӧткузя бока веськыдпельӧса куимпельӧсаӧс h_c судта серти, кодӧс нуӧдӧма веськыд пельӧс йывсянь, да докажитны,^Параллельнӧйяс йылысь аксиоматӧг hc = c/2 ӧткодьлунсӧ докажитны оз позь. — А. В./^ мый h_c = c/2.

9. Вӧчны ӧткузя бокъяса куимпельӧсаӧс h судта серти.^Параллельнӧйяс йылысь аксиоматӧг гӧгӧрвотӧм, кыдзи вӧчны ӧткузя бокъяса куимпельӧсаӧс судта сертиыс. — А. В./^

10. Вӧчны линейка да циркуль отсӧгӧн пельӧсъяс: 1) 90°, 2) 45°, 3) 135°.

V. КУИМПЕЛЬӦСАСА БОКЪЯС ДА ПЕЛЬӦСЪЯС КОСТЫН ЗАВИСИМОСЬТ

1 §. Куимпельӧсалӧн ортсыса пельӧс; сылӧн свойствояс.

1. Урчитӧм. ∠CAD либӧ ∠BAE (74-ӧд серпас), коді артмӧ куимпельӧсаса кутшӧмкӧ куим пиысь ӧти бокӧн да да орчча бок нюжӧдӧм визьысь, шусьӧ куимпельӧсалӧн ортсыс пельӧсӧн. Тадз шуӧны, мед торйӧдны пытшкӧс пельӧсысь, кодӧс артмӧдӧны куимпельӧсаса кык орчча бокъяс.

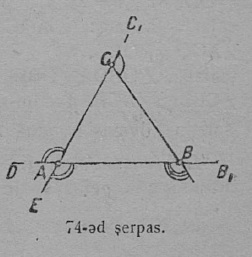
Куимпельӧсаын быд йыв бердӧ позьӧ ӧтисӧ либӧ мӧд боксӧ нюжӧдӧмӧн вӧчны кык ортсыс пельӧс.

Ӧти сійӧ жӧ йыв бердса ортсыс пельӧсъяс, кыдз мӧд-мӧдара пельӧсъяс, ӧтыдждаӧсь, ∠CAD = ∠BAE.

ABC куимпельӧсаын A йыв бердӧ CAD да BAE ортсыс пельӧсъяс вӧчигӧн артмӧ коймӧд пельӧс: ∠DAE, коді оз ло ортсыс пельӧсӧн сы вӧсна, мый сійӧ артмӧ куимпельӧсаса кык орчча бокъяс нюжӧдӧмӧн; тайӧ коймӧд пельӧс ас ыджданас, кыдз противоположнӧй, куимпельӧсаса A йывса пытшкӧс пельӧскӧд ӧтыджда.

2. Ӧти йыв бердса ортсыс пельӧс да пытшкӧс пельӧс — орчча пельӧсъяс; налӧн сумма 2d ыджда, ∠CAD + ∠CAB = 2d.

Тайӧ равенствоысь петӧ: 1) пельӧсъяс пиысь ӧтиыс кӧ ёсь, мӧдыс — тшӧтшыд; 2) пельӧсъяс кӧ ӧтыдждаӧсь, кыкнаныс веськыдӧсь.

3. Теорема. Куимпельӧсалӧн ортсыс пельӧс быд пытшкӧс пельӧсысь, коді сыкӧд абу орчча, ыджыдджык.

Сетӧма: ∆ABC, ∠CBB₁ — ортсыс пельӧс (75-ӧд серпас).

_____________________________________________

Колӧ докажитны: 1) ∠CBB₁ > ∠C; 2) ∠CBB₁ > ∠A.

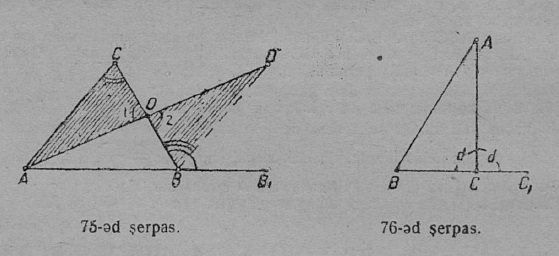
Докажитӧм. Нуӧдам медиана: AO = m_a да сійӧс нюжӧдӧм вылӧ пуктам сы ыджда OD вундӧг. D чут B йывкӧд ӧтлаалӧм бӧрын лоӧ кык куимпельӧса: ∆AOC да ∆BOD; налӧн: 1) CO = OB; 2) AO = OD; 3) ∠1 = ∠2 кыдз противоположнӧй пельӧсъяс; сідзкӧ куимпельӧсаяс ӧтыдждаӧсь: ∆AOC = ∆BOD. Тайӧ равенствоысь петӧ, мый ∠ACO = ∠OBD, но ∠OBD, кыдз ∠CBB₁ ортсыс пельӧслӧн юкӧн, сыысь ичӧтджык, ∠OBD < ∠OBB₁, та вӧсна ∠ACO < ∠OBB₁, либӧ, мый сійӧ жӧ, ∠CBB₁ > ∠ACB. Татшӧм жӧ приёмӧн докажитӧны, мый ∠CBB₁ > ∠A, сӧмын ковмас нуӧдны m_c медиана.

4. Следствийӧ. Куимпельӧсаын кӧ ӧти пельӧс веськыд либӧ тшӧтшыд, мукӧд кык пельӧсыс — ёсьӧсь.

Збыльысь ӧд: 1) ABC куимпельӧсаын кӧ (76-ӧд серп.) ∠C — веськыд, сыкӧд орчча ACC₁ ортсыс пельӧс сідзжӧ веськыд, та вӧсна ∠A < d да ∠B < d, либӧ ∠A да ∠B — ёсь пельӧсъяс; 2) ABC куимпельӧсаын кӧ (77-ӧд серпас) ∠C — тшӧтшыд, сыкӧд орчча ∠ACC₁ ортсыс пельӧсыс — ёсь, та вӧсна ∠A да ∠B — ёсь пельӧсъяс.

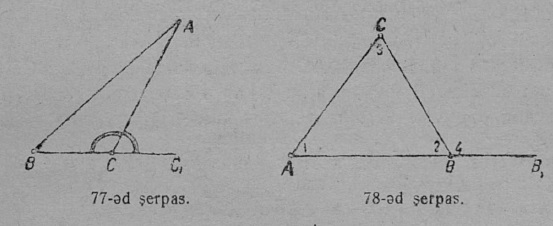
5. Теорема. Быд куимпельӧсаын кык любӧй пытшкӧс пельӧслӧн суммаыс кык веськыд пельӧсысь ичӧтджык.

Сетӧма:

∆ABC да ∠CBB₁, сылӧн ортсыс пельӧс (78-ӧд серпас).

_________________________________________

Колӧ докажитны:

∠A + ∠B < 2d, либӧ ∠A + ∠C < 2d, либӧ ∠B + ∠C < 2d.

Докажитӧм. ∠2 + ∠4 =2d, кыдз орчча пельӧсъяс, та дырйи ∠4 > ∠1 да ∠4 > ∠3.

∠4 + ∠2 = 2d равенствоса шуйгавыв пайысь кӧ ∠4 вежам ичӧтджык пельӧсӧн — ∠1 либӧ ∠3 пельӧсӧн, сумма ичӧтмас да равенство торксяс, лоӧ неравенство:

∠1 + ∠2 < 2d, либӧ ∠A + ∠B < 2d

да

∠3 + ∠2 < 2d, либӧ ∠C + ∠B < 2d.

Та ногӧн жӧ докажитсьӧ, мый ∠1 + ∠3 < 2d.

Теорема лои докажитӧма.

2§. Куимпельӧсаса бокъяс да пельӧсъяс костын зависимосьт.

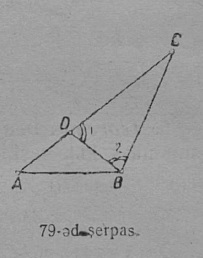
1. Теорема. Быд куимпельӧсаын: 1) ӧтыджда бокъяс водзын куйлӧны ӧтыджда пельӧсъяс, 2) ыджыдджык бок водзын куйлӧ ыджыдджык пельӧс.

I. ∆ABC-ын кӧ AC = CB, сідзкӧ сійӧ — кык ӧткузя бока куимпельӧса да подувтас бердса пельӧсъясыс ӧтыдждаӧсь, ∠B = ∠A; сідзкӧ, ӧти сійӧ жӧ куимпельӧсаын ӧтыджда бокъяс водзын куйлӧны ӧтыджда пельӧсъяс.

∆ABC-ын кӧ AC = AB = CB, сідзкӧ сійӧ ӧткузя бокъяса куимпельӧса; сыын ӧтыджда бокъяс водзын куйлӧны ӧтыджда пельӧсъяс; сы вӧсна, мый сылӧн став бокъясыс ӧтыдждаӧсь, сідзжӧ ӧтыдждаӧсь сылӧн пельӧсъяс. Ӧткузя бокъяса куимпельӧса сідзжӧ шусьӧ ӧтыджда пельӧсъяса куимпельӧсаӧн.

II. Сетӧма: ∆ABC да AC > CB (79-ӧд серп.).

___________________________________

Колӧ докажитны: ∠B > ∠A.

Докажитӧм. Ыджыдджык AC бок вылӧ пуктам вундӧг: CD = CB да D чут ӧтлаалам B йывкӧд, артмас кык ӧткузя бока CBD куимпельӧса, кӧн подувтас бердын пельӧсъяс ӧтыдждаӧсь, ∠1 = ∠2. Но ∠1, кыдз ADB куимпельӧсалӧн ортсыс пельӧс, A пельӧсысь ыджыдджык, ∠1 > ∠A; но ∠1 = ∠2, та вӧсна ∠2 > ∠A; ∠2 ∠ABC-лӧн юкӧн, сідзкӧ ∠ABC ∠A-ысь нӧшта нин ыджыд, ∠B > ∠A.

2. Видзӧдлам теоремаяс, кодъяс лоӧны индӧм теоремаяслы мӧдараӧсь. Индӧм теоремалы мӧдара теоремаӧн шуӧны сэтшӧм теорема, кӧні условийӧнас лоӧ индӧм теоремаса заключенньӧ либӧ заключенньӧлӧн юкӧныс, а заключенньӧнас лоӧ индӧм теоремалӧн условийӧ либӧ условийӧлӧн юкӧн. Пример вылӧ:

1. Быд куимпельӧсаын ӧтыджда бокъяс водзын куйлӧны ӧтыджда пельӧсъяс.

Сетӧма: AC = CB; колӧ докажитны: ∠B = ∠A.

2. Быд куимпельӧсаын ӧтыджда пельӧсъяс водзын куйлӧны ӧтыджда бокъяс.

Сетӧма: ∠B = ∠A; колӧ докажитны: AC = CB.

Тайӧ индӧм кык теоремаысь кӧ мӧдсӧ босьтам мӧдара пыдди, первойяыс сы серти кутас шусьыны веськыд теоремаӧн.

Тайӧ примерын кыкнан теоремаыс веськыд.^тані “веськыд — верная”/^ Но тайӧ абу пыр тадз. Веськыд^тані “веськыд — прямая”/^ теоремаӧс кӧ докажитӧма, оз на позь вӧчны заключенньӧ, мый мӧдара теорема лоӧ справедливӧй. Пример, босьтам татшӧм веськыд теорема: “кык противоположнӧй пельӧсъяс ӧтыдждаӧсь” справедливӧй, а сылы мӧдара теоремаыс: “кык пельӧс кӧ ӧтыдждаӧсь, найӧ — противоположнӧй пельӧсъяс” абу век веськыд.

3. Теорема (мӧдара). Быд куимпельӧсаын ӧтыджда пельӧсъяс водзын куйлӧны ӧтыджда бокъяс.

Сетӧма: ∆ABC да ∠B = ∠A.

_______________________

Колӧ докажитны: AC = BC.

Докажитӧм (паныдсянь). Колӧ докажитны: AC = BC. Мӧвпыштам намӧдарӧ, шуам, мый AC абу равнӧй BC-лы, а BC-ысь ыджыдджык, AC > BC.

Шуам кӧ, мый AC > BC, тась петӧ, мый ∠B > ∠A сы вӧсна, мый куимпельӧсаын ыджыдджык бок водзын куйлӧ ыджыдджык пельӧс. Артмӧм вывод противоречитӧ теорема условийӧлы, мый ∠A = ∠B, и миян шулӧмным, мый AC > BC, лоны вермытӧмтор; татшӧм жӧ заключенньӧӧ воам, кор шулам, мый AC < BC.

Сідзкӧ, кор ∠A = ∠B, оз вермы лоны, мед AC вӧлі BC-ысь ыджыдджык либӧ ичӧтджык. AC кӧ оз вермы лоны BC-ысь ыджыдджыкӧн ни ичӧтджыкӧн, сылы колӧ лоны BC-кӧд ӧтыдждаӧн. Сідзкӧ, AC = BC.

4. Теорема (мӧдара). Быд куимпельӧсаын ыджыдджык пельӧс водзын куйлӧ ыджыдджык бок.

Сетӧма: ∆ABC да ∠B > ∠A (79-ӧд серп.).

__________________________________

Колӧ докажитны: AC > BC.

Докажитӧм (паныдсянь). Колӧ докажитны AC > BC. Мӧвпыштам намӧдарӧ, мед, шуам, AC абу ыджыдджык CB-ысь, да видзӧдлам вермыны лоан кык случай: 1) AC = CB либӧ 2) AC < CB.

Миян шулӧмсьыным, мый AC = CB, петӧ, мый ∠B = ∠A, но тайӧ вывод противоречитӧ теорема условийӧлы, мый серти ∠B > ∠A, и шулӧмным, мый AC = CB, та вӧсна лоны вермытӧмтор; мӧд ног шулӧмсьыным, мый AC < CB, петӧ, мый сэк ∠A > ∠B, тайӧ бара жӧ противоречитӧ теорема условийӧлы сы вӧсна, мый ∠B > ∠A. Воам выводӧ, мый, кор ∠B > ∠A, сэк AC > CB.

5. Следствийӧяс. 1. Веськыдпельӧса куимпельӧсаын гипотенуза быд катетысь ыджыдджык.

2. Тшӧтшыдпельӧса куимпельӧсаын тшӧтшыд пельӧс водзын куйлысь бокыс медыджыд.

Юасянъяс да упражненньӧяс.

1. Кутшӧм куимпельӧсаын ортсыс пельӧс ас орчча пытшкӧс пельӧсыскӧд ӧтыджда?

2. Мый вӧсна веськыдпельӧса куимпельӧсаын быд катет гипотенузаысь ичӧтджык? Мый вӧсна кык катетлӧн сумма ыджыдджык гипотенузаысь? Кутшӧм теоремаяс ковмасны ӧтвет вылӧ?

3. ABC куимпельӧсаын AB бок = 18 см, BC = 22 см, AC = 20 см. Куимпельӧсаын кутшӧм пельӧс медыджыд? Кутшӧм медічӧт?

4. ABC куимпельӧсаын ∠A = 60°, ∠B = 80°, ∠C = ∠40°. Индыны куимпельӧсалысь медыджыд да медічӧт бокъяс.

VI. ПЕРПЕНДИКУЛЯР ДА ПӦЛЫНЯ ВИЗЬЯС.

1 §. Чутлӧн веськыд визь вылӧ проекция.

1. Теорема. Веськыд визь сайса чутсянь веськыд визь вылӧ позьӧ нуӧдны сӧмын ӧти перпендикуляр.

Сетӧма:

MN веськыд визь, сы сайын A чут, AB ⊥ MN (80 серп.).

____________________________________________

Колӧ докажитны:

AB лоӧ MN веськыд визь вылӧ A чутсянь сӧмын ӧти перпендикуляр.

Докажитӧм (паныдсянь). Шуам, мый A чутсянь MN веськыд вылӧ, AB перпендикулярысь ӧтдор, нуӧдӧма нӧшта AC перпендикуляр. Артмас ∆ABC, кӧн лоӧ кык веськыд пельӧс, — но татшӧмтор лоны оз вермы сы вӧсна, мый куимпельӧсаын кык пельӧслӧн суммаыс кык веськыд пельӧсысь век ичӧтджык. Сідзкӧ, шуӧмным, мый MN веськыд вылӧ A чутсянь, AB перпендикулярысь ӧтдор, позьӧ нуӧдны нӧшта мӧд AC перпендикуляр, оз вермы лоны; сідзкӧ, A чутсянь, кодӧс босьтӧма веськыд визь сайын, веськыд визь вылӧ позьӧ нуӧдны сӧмын ӧти перпендикуляр.

2. AB перпендикулярлӧн B подувтасыс шусьӧ MN веськыд вылӧ A чутлӧн проекция. Чутлӧн веськыд визь вылӧ проекция эм чут.

Гӧгӧрвоана, мый AB перпендикулярлӧн подувтасыс B чут лоӧ проекцияӧн оз сӧмын AB перпендикулярса A чутлӧн, а любӧй чутлӧн, кодӧс босьтан AB перпендикуляр вылын, на костӧ тшӧтш пырӧ B чут, коді куйлӧ ӧттшӧтш AB перпендикуляр вылын дай MN веськыд вылын.

2 §. Перпендикуляр да пӧлыня визьяс.

1. AB кӧ MN-лы перпендикуляр, то став мукӧд веськыд визьяс, кодъяс A чутӧс ӧтлаалӧны MN веськыд визь вывса чутъяскӧд, шусьӧны пӧлыня визьясӧн. AC, AD, AE — пӧлыняяс (80 серп.).

2. Теорема. Сайса чутсянь кӧ сетӧм веськыд визь вылӧ нуӧдны перпендикуляр да пӧлыня визь, перпендикулярыс лоӧ быд пӧлыняысь дженьыдджык.

Сетӧма: AB ⊥ MN да AC — пӧлыня (80 серп.).

______________________________________

Колӧ докажитны: AB < AC.

Докажитӧм. AB перпендикуляр да AC пӧлыня визьыс — веськыдпельӧса ABC куимпельӧсалӧн бокъяс: AB перпендикулярыс — катет, AC пӧлыня визьыс — гипотенуза.

AC гипотенуза AB катетысь ыджыдджык, та вӧсна AB < AC.

Вывод. Перпендикуляр лоӧ чутсянь веськыд визьӧдз медматысса коластӧн.

Индӧд. Кор шуӧны “чутсянь веськыд визьӧдз коласт”, сэк век гӧгӧрвоӧны медся дженьыд коластсӧ, кодӧс мурталӧны сетӧм чутсянь сетӧм веськыдӧдз перпендикуляр кузьтаӧн; мӧд ногӧн, вундӧгӧн, кодлӧн помъясыс — сетӧм чут да сетӧм веськыд вылын сылӧн проекция.

3 §. Пӧлыняяс да налӧн проекцияяс.

1. MN веськыдлӧн BC вундӧг, кодлӧн помъясыс лоӧны AB перпендикулярлӧн да AC пӧлынялӧн B да C подувтасъяс (80 серп.), шусьӧ AC пӧлынялӧн проекцияӧн.

2. Теорема. 1) Ӧти сійӧ жӧ чутысь веськыд визь вылӧ нуӧдӧм пӧлыняяс ӧтыдждаӧсь сэк, кор налӧн проекцияясыс ӧтыдждаӧсь.

2) Ӧти сійӧ жӧ чутысь веськыд визь вылӧ нуӧдӧм кык пӧлыня пиысь сійӧыс ыджыдджык, кодыслӧн тайӧ веськыд визьыс вылӧ проекцияыс ыджыдджык.

1) Сетӧма: AB ⊥ MN да BC = BD (80 серп.),

________________________________

Колӧ докажитны: AC = AD.

2) Сетӧма: AB ⊥ MN да BE > BC.

_________________________

Колӧ докажитны: AE > AC.

Докажитӧм: 1) ABC да ABD куимпельӧсаясыс веськыдпельӧсаӧсь, налӧн AB — ӧтувъя бок да условийӧ серти BC = BD, сідзкӧ, найӧ ӧтыдждаӧсь, та вӧсна AC = AD.

2) Условийӧ серти BE > BC; BE вундӧг вылӧ B чутсянь пуктам BD = BC вундӧг да A-кӧд ӧтлаалам D, лоӧ пӧлыня визь AD = AC. Видзӧдлам ∆AED; сылӧн ∠ADE — тшӧтшыд, кыдзи веськыд пельӧса ABD куимпельӧсалӧн ортсыс пельӧс, сідзкӧ ∠ADE > ∠AED, та вӧсна AE > AD, либӧ AE > AC, сы вӧсна, мый AC = AD.

3. Теорема (мӧдара). Ӧти сійӧ жӧ чутсянь веськыд визь вылӧ нуӧдӧм пӧлыняяс кӧ ӧтыдждаӧсь, сідзкӧ ӧтыдждаӧсь сійӧ жӧ веськыд визь вылас налӧн проекцияяс.

Сетӧма: AB ⊥ MN да AC = AD (80 серп.).

_______________________________

Колӧ докажитны: BC = BD.

Докажитӧм (паныдсянь). Шуам, мый BC > BD, сэк AC > AD, но тайӧ паныдасьӧ условийӧлы, кӧн шуӧма, мый AC = AD; та вӧсна миян шуӧмным веськыдӧн оз вермы лоны; шуам, мый BC < BD, сэк AC < AD; тайӧ сідзжӧ паныдасьӧ условийӧлы, сідзкӧ миян шуӧмным бара оз туй. BC оз вермы лоны BD-ысь ыджыдджыкӧн ни ичӧтджыкӧн; сідзкӧ BC = BD.

4. Теорема (мӧдара). Ӧти сійӧ жӧ чутсянь веськыд визь вылӧ нуӧдӧм не ӧтыджда кык пӧлыня визьысь ыджыдджыкыслӧн ыджыдджык и проекцияыс.

Сетӧма: AB ⊥ MN, AE > AD (80 серп.).

____________________________

Колӧ докажитны: BE > BD.

Докажитӧм (паныдсянь). Шуам, мый BE абу ыджыдджык BD-ысь, сэк вермас лоны кык случай: BE = BD либӧ BE < BD. Босьтны кӧ первойя шуӧмнымӧс, лоӧ AE = AD, но тайӧ паныдасьӧ условийӧлы, мый серти AE > AD; первойя шуӧмным оз туй; шуны кӧ, мый BE < BD, лоӧ AE < AD, мый бара оз туй. BE оз вермы лоны BD ыджда ни BD-ысь ичӧтджык, та вӧсна BE вермӧ лоны BD-ысь сӧмын ыджыдджык, BE > BD, мый вӧлі и колӧ докажитны.

4 §. Веськыдпельӧса куимпельӧсаяслӧн равенство.

Видлалам веськыдпельӧса куимпельӧсаяслысь равенство кузя нӧшта кык признак.

1. Теорема. Веськыдпельӧса куимпельӧсаяс ӧтыдждаӧсь, кор ӧти куимпельӧсалӧн гипотенуза да ёсь пельӧс ӧтыдждаӧсь мӧд куимпельӧсаса гипотенузакӧд да ёсь пельӧскӧд.

Сетӧма:

∆ABC да ∆A₁B₁C₁; A₁B₁ = AB; ∠B₁ = ∠B (81 серп.).

__________________________________________

Колӧ докажитны: ∆A₁B₁C₁ = ∆ABC.

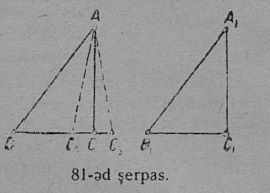
Докажитӧм. ∆A₁B₁C₁ пуктам ∆ABC вылӧ сідз, мед A₁B₁ да AB гипотенузаяс вевсяасясны, сэк B да B₁ пельӧсъяс равенство серти B₁C₁ бок мунас BC бок кузя. Юассьӧ, BC веськыд визь вывса кутшӧм чутӧ усьӧ C₁ чут? Вермас лоны куим случай: C₁ чут усьӧ C чутсянь шуйгавылӧ, либӧ сысянь веськыдвылӧ, либӧ, медбӧрын, сыкӧд ӧтлаасяс. Мед C₁ чут C чутсянь уси шуйгавылӧ, сэк A₁C₁ катет мунас AC₂ кузя; та ногӧн лои эськӧ, мый A чутсянь BC веськыд визь вылӧ нуӧдӧма кык перпендикуляр — AC да AC₂, татшӧмтор лоны оз вермы сы вӧсна, мый сайса чутсянь веськыд визь вылӧ позьӧ нуӧдны сӧмын ӧти перпендикуляр. Татшӧм жӧ выводӧ воам сэк, кор шуам, мый C₁ чут усьӧ C чутсянь веськыдвылӧ. C₁ чут оз вермы усьны C чутсянь шуйгавылӧ ни веськыдвылӧ; C₁ чут да C чут вермӧны сӧмын вевсяасьны. Тадз, ABC куимпельӧса вылӧ ∆A₁B₁C₁ пуктігӧн сыкӧд ӧтлаасьӧ, сідзкӧ найӧ ӧтыдждаӧсь.

Следствийӧ. Равнӧй куимпельӧсаяслӧн равнӧйӧсь и соответственнӧй судтаясныс.

Сетӧма:

∆A₁B₁C₁ = ∆ABC; C₁D₁ да CD — налӧн судтаяс (82 серп.).

________________________________________________

Колӧ докажитны: C₁D₁ = CD.

Докажитӧм. Видлалам ∆A₁C₁D₁ да ∆ACD; тайӧ куимпельӧсаясыс — веськыдпельӧсаӧсь; найӧ мӧда-мӧдкӧд ӧтыдждаӧсь сы вӧсна, мый налӧн A₁C₁ = AC да ∠A₁ = ∠A; A₁C₁D₁ да ACD куимпельӧсаяс равенствоысь петӧ, мый C₁D₁ = CD, м. л. A₁B₁C₁ да ABC куимпельӧсаяслӧн судтаясыс равнӧйӧсь.

2. Теорема. Веськыдпельӧса куимпельӧсаяс равнӧйӧсь сэк, кор ӧти куимпельӧсалӧн гипотенузаыс да катетыс соответственнӧ равнӧйӧсь мӧд куимпельӧсаса гипотенузалы да катетлы.

Сетӧма:

∆A₁B₁C₁ да ∆ABC; A₁B₁ = AB; A₁C₁ = AC (83 серп.).

___________________________________________

Колӧ докажитны: ∆A₁B₁C₁ = ∆ABC.

Докажитӧм. ∆A₁B₁C₁ пуктам ABC куимпельӧса бердӧ сідз, мед ӧтыджда A₁C₁ да AC катетъяс вевсяасясны — артмас фигура ABCD. Видлалам 1 да 2 пельӧсъяс C чут бердысь. ∠1 + ∠2 = 2d сы вӧсна, мый кыкнаныс веськыд пельӧсъяс; сідзкӧ ∠BCD — павтыртӧм пельӧс, та вӧсна BC да CD артмӧдӧны ӧти веськыд визь; урчитам, мый артмӧм фигураыс — куимпельӧса; но тайӧ куимпельӧсаын AB = AD, та вӧсна сійӧ кык ӧткузя бока, сылӧн AC судтаыс юкӧ сійӧс кык ӧтыджда куимпельӧсаӧ: ∆ABC = ∆ACD, сідзкӧ, ∆A₁B₁C₁ = ∆ABC.

Юасянъяс да упражненньӧяс.

1. Кык ӧткузя бока куимпельӧсалӧн подувтасыс a см ыджда. Ыджыд-ӧ сійӧ боквывса бокыслӧн подувтасыс вылӧ проекция?

2. Веськыдпельӧса куимпельӧсалӧн ӧти катет a см, а мӧд — b см ыджда. Ыджыдӧсь-ӧ гипотенузалӧн быд катет вылӧ проекцияяс?

3. Тшӧтшыдпельӧса куимпельӧсаын нуӧдны судта тшӧтшыд пельӧс вӧчысь бокъяс пиысь кодыс вылӧ кӧ.

4. Произвольнӧй формаа ABC куимпельӧсаын нуӧдӧма AD биссектриса. Докажитны, мый AD биссектрисалӧн AB да AC бокъяс вылӧ проекцияяс ӧтыдждаӧсь.

5. AD — BAC пельӧслӧн биссектриса. Докажитны, мый биссектриса вылын босьтӧм любӧй чутыс пельӧс бокъяссянь ӧтылнаын.

6. Сетӧма MN веськыд визь, сы сайын кык чут A да B. MN веськыд вылын корсьны чут, мед сійӧ вӧлі A да B чутъяссянь ӧтылнаын.

VII. ПАРАЛЛЕЛЬНӦЙ ВЕСЬКЫД ВИЗЬЯС.

1 §. Параллельнӧй веськыд визьяс.

1. Кык веськыд визь: AB да CD, кодъяс куйлӧны ӧти сійӧ жӧ плоскосьт вылын, вермасны относительнӧ мӧда-мӧдлы босьтавны различнӧй положенньӧяс; найӧ вермасны мӧда-мӧдкӧд либӧ вомӧнасьны, либӧ вевсяасьны, либӧ не вомӧнасьны.

1) Сійӧ случайын, кор кык веськыд визь: AB да CD вомӧнасьӧны, налӧн эм ӧти ӧтувъя P чут — вомӧнасян чут; сійӧ ӧтувъя кыкнан веськыдыслӧн да ӧттшӧтш куйлӧ кыкнаныс вылын.

2) Сійӧ случайын, кор кык веськыд визьлӧн абу сӧмын ӧти ӧтувъя чут, а эм кык ӧтувъя чут, найӧ ӧтлаасьӧны сы вӧсна, мый кык чут костті позьӧ нуӧдны сӧмын ӧти веськыд визь, та вӧсна ӧти веськыдлӧн любӧй чут лоӧ мӧд веськыдвывса ӧти кутшӧмкӧ чутӧн.

3) Медбӧрын, кор кык AB да CD веськыдъяслӧн (84 серп.), кодъяс куйлӧны ӧти сійӧ жӧ плоскосьт вылын, абу ни ӧти ӧтувъя чут, найӧ оз вомӧнасьны, сэсся кӧть кытчӧдз огӧ нюжӧдӧй кӧть кодарланьӧ, найӧ оз вевсяасьны нин. Татшӧм веськыд визьясыс шусьӧны параллельнӧйясӧн.

Урчитӧм. Веськыд визьяс, кодъяс куйлӧны ӧти плоскосьт вылын да кӧть кодарлань нюжӧдігӧн кӧ оз вомӧнасьны, шусьӧны параллельнӧйясӧн.

Параллельнӧй веськыд визьяс вылӧ примеръясӧн лоӧны: кӧрт туйлӧн рельсъяс, веськыд нёльпельӧса формаа пызан пӧвлӧн воча-воча доръяс, кык отвес да с. в.

Веськыдъяслысь параллельносьт пасйӧм вылӧ употребляйтӧны пас ∥; гижӧд AB ∥ CD лыддьыссьӧ: AB веськыд CD веськыдлы параллельнӧй.

2. Мый параллельнӧй веськыд визьяс эмӧсь, ми убеждайтчам быдлунъя олӧманым миян гӧгӧрса предметъяс бӧрся наблюдайтігӧн, но позьӧ докажитны тшӧтш и теорияӧн.

Теорема. Кык веськыд визь, кодъяс лоӧны сійӧ жӧ ӧти коймӧд веськыдлы перпендикуляръясӧн, оз вомӧнасьны — найӧ параллельнӧйӧсь.

Сетӧма: AB ⊥ MN, CD ⊥ MN (85 серп.).

_______________________________

Колӧ докажитны: AB ∥ CD.

Докажитӧм (паныдсянь). Шуам, мый MN веськыдлы AB да CD перпендикулярнӧй веськыдъяс, кор найӧс нюжӧдан, кутшӧмкӧ P чутын вомӧнасясны; сэк лоӧ, мый ӧти P чутсянь MN веськыд визь вылӧ нуӧдӧма кык перпендикуляр, AB да CD, но тайӧ лоны оз вермы сы вӧсна, мый ӧти чутсянь веськыд визь вылӧ позьӧ нуӧдны сӧмын ӧти перпендикуляр; сідзкӧ, татшӧм шуӧмным, мый AB да CD вомӧнасясны, оз туй; AB да CD, кодъяс MN веськыдлы перпендикуляръяс, вомӧнасьны оз вермыны; сідзкӧ, найӧ параллельнӧйӧсь, — AB ∥ CD.

Задача. Сетӧма MN веськыд визь, сы сайын K чут. K чут пыр нуӧдны веськыд визь, мед сійӧ вӧлі MN веськыдлы параллельнӧй.

Построенньӧ. Сетӧм K чут пыр нуӧдам MN веськыдлы KP перпендикуляр, сэсся K чутсянь — KP веськыдлы KL перпендикуляр. KL — корсян веськыд визь сы вӧсна, мый KL да MN кык веськыд визь, кодъяс KP веськыдлы перпендикулярнӧйӧсь, — KL ∥ MN.

2 §. Параллельнӧйяс йылысь аксиома.

1. Ми тӧдмалім, мый MN веськыд визь сайын сетӧм K чут пыр позьӧ MN веськыдлы нуӧдны параллельнӧй веськыдӧс. Колӧ вӧлі нӧшта докажитны, мый тадз нуӧдӧм KL веськыд визь лоӧ сӧмын ӧти веськыд визьӧн, коді мунӧ K чут пыр да MN веськыдкӧд параллельнӧй. Но тайӧ положенньӧсӧ докажитны он вермы, сійӧс колӧ босьтны кыдз аксиомаӧс; тадзикӧн и вӧчисны важ греческӧй геометръяс зэв на водз миян эраӧдз. Став кадса да став йӧзса медбур геометръяс вель унаысь кутчысявлісны тайӧ положенньӧ докажитны, но успех эз ло. Сӧмын колян XІX сё воын ыджыд математик Гаусс да мукӧд установитісны, мый логическӧй туйӧн тӧдана геометрическӧй аксиомаясӧн да теоремаясӧн оз позь докажитны, мый веськыд визь сайын сетӧм чут пыр позьӧ нуӧдны сӧмын ӧти веськыд, код мед вӧлі сетӧм веськыд визькӧд параллельнӧй; тайӧ положенньӧ колӧ босьтны кыдз тыдаланаӧс; сылӧн веськыдлуныс оправдывайтчӧ непосредственнӧй наблюденньӧясӧн да векӧвӧйя опытӧн.

Аксиома. Плоскосьт вылын веськыд визь сайын сетӧм чут пыр позьӧ нуӧдны сӧмын ӧти веськыдӧс, коді сетӧм веськыдлы лоӧ параллельнӧй.

Следствийӧяс. 1. Веськыд визь кӧ кык параллельнӧй визь пиысь вундӧ ӧтисӧ, сідзжӧ сійӧ вундас и мӧдсӧ.

Сетӧма: AB ∥ CD; K чутын MN вундӧ AB (87 серп.).

_________________________________________

Колӧ докажитны: MN вундӧ CD.

Докажитӧм (паныдсянь). Шуам, мый MN веськыд визь, коді AB-кӧд вомӧнасьӧ K чутын, CD веськыдкӧд оз вомӧнась. Тайӧ кӧ тадз, MN-лы колӧ лоны CD-кӧд параллельнӧйӧн, сэк лоӧ, мый K чут пыр мунӧны CD-кӧд параллельнӧйяс AB да MN кык веськыд визь, но тайӧ паныдасьӧ параллельнӧйяс йылысь аксиомалы; сідзкӧ миян шуӧмным, мый, AB веськыдысь ӧтдор, K чут пыр мунӧ нӧшта мӧд веськыд визь, MN, коді CD веськыдкӧд оз вомӧнась, оз туй. Сідзкӧ, MN веськыд визь CD-кӧд абу параллельнӧй, сылы колӧ сыкӧд вомӧнасьны.

2. Кык веськыд визь кӧ торйӧн-торйӧн параллельнӧйӧсь коймӧд веськыдлы, найӧ параллельнӧйӧсь мӧда-мӧдыскӧд.

Сетӧма: AB ∥ EF да CD ∥ EF (88 серп.).

_______________________________

Колӧ докажитны: AB ∥ CD.

Докажитӧм (паныдсянь). Шуам, мый AB да CD веськыдъяс абу параллельнӧйӧсь да кутшӧмкӧ P чутын вомӧнасьӧны. Татысь ми воам выводӧ, мый P чут пыр мунӧны кык различнӧй — AB да CD — веськыдъяс, кодъяс параллельнӧйӧсь EF веськыдлы; но тайӧ паныдасьӧ параллельнӧйяс йылысь аксиомалы; сідзкӧ, миян шуӧмным оз туй. Та вӧсна EF веськыдкӧд параллельнӧйяс — AB да CD — веськыдъяс оз вермыны вомӧнасьны; найӧ параллельнӧйӧсь: AB ∥ CD.

3 §. Кык параллельнӧйӧн да найӧс вундысьӧн артман пельӧсъяс.

1. AB веськыд кӧ (89 серп.) вундӧ кутшӧмкӧ веськыдӧс, шуам CD, сійӧ сыкӧд вӧчӧ 4 пельӧс, кодъяс пиын кык ёсь да кык тшӧтшыд; кыкнан ёсь да кыкнан тшӧтшыд пельӧсъясыс ӧтыдждаӧсь мӧда-мӧдныскӧд, кыдз противоположнӧйяс: ∠1 = ∠3; ∠2 = ∠4.

Таысь ӧтдор, любӧй ёсь пельӧс да любӧй тшӧтшыд пельӧс суммааныс сетӧны 2d, кыдзи орчча пельӧсъяс:

∠1 + ∠2 = 2d; ∠3 + ∠4 = 2d;

∠2 + ∠3 = 2d; ∠1 + ∠4 = 2d.

Вомӧнасян AB да CD веськыдъяс кӧ мӧда-мӧдлы перпендикуляръяс, став наӧн артман пельӧсъяс мӧда-мӧдкӧд ӧтыдждаӧсь да быд пельӧс на пиысь — веськыд.

2. EF веськыд кӧ (90 серп.) вундӧ оз ӧти веськыдӧс, а кык — AB да CD — веськыдӧс, AB да CD веськыдъяскӧд EF веськыдлӧн вомӧнасян чутъяс бердын артмӧ кӧкъямыс пельӧс: AB веськыдкӧд вомӧнасян M чут бердын ӧтувъя йыла нёль пельӧс да CD веськыдкӧд вомӧнасян N чут бердын ӧтувъя йыла нёль пельӧс. EF веськыд, коді вундӧ AB да CD веськыдъясӧс, шусьӧ вундысьӧн. Торъя сикас пельӧс гозъяс видлалӧм могысь, кодъяс пиысь ӧтиыс M чут бердын, а мӧдыс — N чут бердын, пельӧсъяслы пукталӧма торъя нимъяс, сы серти, кыдзи найӧ куйлӧны вундысь серти.

1) Пельӧсъяс, кодъяс куйлӧны AB да CD веськыдъяс костын да EF вундыссянь ӧтар бокын, шусьӧны пытшкӧс ӧтарбокса пельӧсъясӧн. Найӧ: ∠3 да ∠6; ∠4 да ∠5.

2) Пельӧсъяс, кодъяс куйлӧны AB да CD веськыдъяс сайын да EF вундыссянь ӧтар бокын, шусьӧны ортсыс ӧтарбокса пельӧсъясӧн. Найӧ: ∠1 да ∠8; ∠2 да ∠7.

3) Пельӧсъяс, кодъяс куйлӧны AB да CD веськыдъяс костын да EF вундыссянь разнӧй бокъясын, шусьӧны пытшкӧс крестӧнкуйлысь пельӧсъясӧн. Найӧ: ∠3 да ∠5; ∠4 да ∠6.

4) Пельӧсъяс, кодъяс куйлӧны AB да CD веськыдъяс сайын да EF вундыссянь разнӧй бокъясын, шусьӧны ортсыс крестӧнкуйлысь пельӧсъясӧн. Найӧ: ∠1 да ∠7; ∠2 да ∠8.

5) Пельӧсъяс, кодъяс куйлӧны EF вундыссянь ӧтар бокын да кодъяс пиысь ӧтиыс пытшкӧс, а мӧдыс ортсыс, шусьӧны соответственнӧй пельӧсъясӧн. Найӧ: ∠1 да ∠5; ∠2 да ∠6; ∠3 да ∠7; ∠4 да ∠8.

3. Индӧм пельӧс гозъяс пиысь кутшӧмкӧ ӧти гозса пельӧсъяс костын определённӧй зависимосьт ас бӧрсяньыс кыскӧ быд мӧд гозса пельӧсъяс костысь определённӧй зависимосьт.

Теорема. Кык веськыд визь коймӧд веськыдкӧд вомӧнасигӧн кӧ соответственнӧй пельӧсъяс ӧтыдждаӧсь, то: 1) мӧда-мӧдкӧд ӧтыдждаӧсь пытшкӧс либӧ ортсыс крестӧнкуйлысь пельӧсъяс; 2) пытшкӧс либӧ ортсыс ӧтарбокса пельӧсъяслӧн суммаыс 2d ыджда.

Сетӧма:

AB да CD веськыдъяс да EF вундысь; ∠1 = ∠5 (91 серп.).

_______________________________________________

Колӧ докажитны:

1) а) ∠3 = ∠5 да ∠1 = ∠7;

b) ∠4 = ∠6 да ∠2 = ∠8;

2) а) ∠4 + ∠5 = 2d да ∠3 + ∠6 = 2d;

b) ∠1 + ∠8 = 2d да ∠2 + ∠7 = 2d.

Докажитӧм. 1а) ∠1 = ∠5 условийӧ серти, ∠1 = ∠3, кыдз противоположнӧйяс, сідзкӧ, ∠3 = ∠5, сы вӧсна, мый, кор кык величина ∠3 да ∠5 торйӧн ӧтыдждаӧсь коймӧдкӧд, либӧ ∠1, найӧ ӧтыдждаӧсь мӧда-мӧдкӧд.

Сідзкӧ, соответственнӧй пельӧсъяс кӧ, ∠1 да ∠5, ӧтыдждаӧсь, ӧтыдждаӧсь пытшкӧс крестӧнкуйлысь пельӧсъяс, ∠3 = ∠5. Тадз жӧ докажитӧны, мый кор ∠1 = ∠5, сэк ∠1 = ∠7.

1b) Условийӧ серти ∠1 = ∠5; ∠1 дінӧ кӧ содтыны ∠4 да ∠5 дінӧ кӧ содтыны ∠6, ∠1 + ∠4 = 2d да ∠5 + ∠6 = 2d, кыдз орчча пельӧсъяс. Кык ӧтыджда пельӧсъяс дінӧ, ∠1 да ∠5 дінӧ, содтім ӧти пельӧсӧн да кыкнанас сумма лои ӧти сійӧ жӧ: 2d; тадз вермас лоны сӧмын сэк, кор ∠4 = ∠6; тайӧ петкӧдлӧ, мый пытшкӧс крестӧнкуйлысь пельӧсъяс ӧтыдждаӧсь. Тадз жӧ докажитӧны, мый, кор ∠1 = ∠5, сэк ∠2 = ∠8.

2a) Условийӧ серти ∠1 = ∠5; ∠1 + ∠4 = 2d кыдз орччаяс. Бӧръя равенствоын ∠1 вежам сыкӧд ӧтыджда ∠5-ӧн, лоӧ, мый ∠5 + ∠4 = 2d: пытшкӧс ӧтарбокса пельӧсъяслӧн сумма 2d ыджда. Тадз жӧ докажитӧны, мый, кор ∠1 = ∠5, сэк ∠3 + ∠6 = 2d.

2b) Условийӧ серти ∠1 = ∠5; ∠5 + ∠8 = 2d кыдз орччаяс. Бӧръя равенствоын ∠5 вежам сыкӧд ӧтыджда ∠1-ӧн, лоӧ ∠1 + ∠8 = 2d: ортсыс ӧтарбокса пельӧсъяслӧн сумма 2d ыджда. Тадз жӧ докажитӧны, мый, кор ∠1 = ∠5, сэк ∠2 + ∠7 = 2d.

4 §. Веськыд визьяс параллельносьт йылысь признакъяс.

1. Кык веськыд визь параллельносьт йылысь признакъяс пиысь ӧти лоӧ: кык веськыд лоӧны параллельнӧйӧсь, кор найӧ ӧти сійӧ жӧ коймӧд веськыдлы перпендикулярнӧйӧсь. Видзӧдлам мукӧд признакъяс, кодъясӧс подулалӧма пельӧсъяс свойствояс вылын, кор пельӧсъясыс артмӧны кык веськыд визьӧс коймӧд веськыдӧн вомӧналігӧн.

Теорема. Коймӧдӧн вундӧм кык веськыд визь сэк параллельнӧйӧсь, кор 1) пытшкӧс либӧ ортсыс крестӧнкуйлысь пельӧсъясыс ӧтыдждаӧсь; 2) соответственнӧй пельӧсъяс ӧтыдждаӧсь; 3) пытшкӧс либӧ ортсыс ӧтарбокса пельӧсъяслӧн сумма 2d ыджда.

Докажитам тайӧ теоремалысь 1 юкӧн.

Сетӧма:

AB да CD веськыдъяс; EF — вундысь; ∠1 = ∠2 (92 серп.).

______________________________________

Колӧ докажитны: AB ∥ CD.

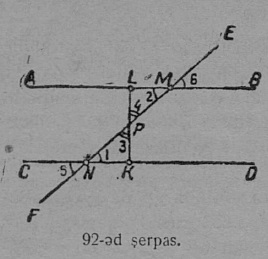
Докажитӧм. EF вундысь AB да CD веськыдъясӧс вомӧналӧ M да N чутъясын. MN вундӧг юкам шӧри да P шӧр пыр нуӧдам CD-лы перпендикуляр — PK; нюжӧдам тайӧ перпендикуляр AB веськыдкӧд L чутын вомӧнасьтӧдз; артмас кык куимпельӧса: ∆PLM да ∆PKN. Тайӧ куимпельӧсаясын: 1) PM = PN — построенньӧ серти; 2) ∠1 = ∠2 — условийӧ серти, 3) ∠3 = ∠4, кыдз противоположнӧй пельӧсъяс; сідзкӧ, ∆PLM = ∆PKN. Найӧ равенствоысь петӧ, мый ∠K = ∠L; сы вӧсна, мый PK ⊥ CD — построенньӧ серти, ∠K = d, сідзкӧ и ∠L = d; тайӧ лоӧ, мый PL ⊥ AB. Татысь петӧ, мый AB да CD веськыдъяс перпендикулярнӧйӧсь ӧти сійӧ жӧ коймӧд KL веськыдлы; сідзкӧ, найӧ параллельнӧйӧсь, AB ∥ CD.

Теорема докажитӧм сійӧ случайлы, кор ӧтыдждаӧсь ортсыс крестӧнкуйлысь пельӧсъяс, шуам ∠5 = ∠6, вайӧдчӧ видлалӧм случайӧ.

Сетӧма, мый ∠5 = ∠6. Сы вӧсна, мый ∠5 = ∠1 да ∠6 = ∠2, кыдз противоположнӧй пельӧсъяс, ∠1 = ∠2; тайӧ пельӧсъяс — пытшкӧс крестӧнкуйлысь пельӧсъяс, кодъяс мӧда-мӧдкӧд ӧтыдждаӧсь, та вӧсна AB ∥ CD.

Аналогичнӧя докажитӧны теоремаяс, кор сетӧма, мый соответственнӧй пельӧсъяс ӧтыдждаӧсь; либӧ сетӧма, мый пытшкӧс либӧ ортсыс ӧтарбокса пельӧсъяслӧн суммаыс 2d ыджда.

Задача. Нуӧдны веськыд визь, мед сійӧ муніс K чут пыр да вӧлі сетӧм MN веськыдлы параллельнӧй (93 серп.).

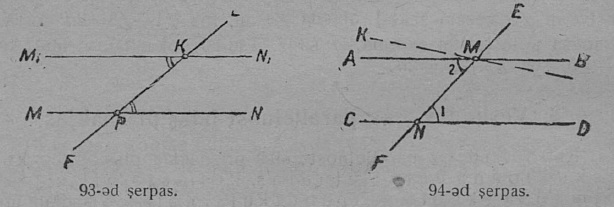
Построенньӧ. Сетӧма MN веськыд, сы сайын K чут. K чут пыр нуӧдам произвольнӧй пельӧсӧн MN-ӧс вундысьӧс — EF; EF вундысь MN веськыдкӧд вӧчӧ ∠KPN; K чут бердӧ EF вундысь мӧдарӧ вӧчам ∠M₁KP = ∠KPN. ∠M₁KP-лӧн M₁K дор лоӧ корсян MN-лы веськыд параллельнӧй, M₁K ∥ MN. Тайӧ сы вӧсна, мый ∠M₁KP = ∠KPN, кодъяс — пытшкӧс крестӧнкуйлысь пельӧсъяс, сідзкӧ M₁N₁ ∥ MN.

2. Теорема (мӧдара). Кор кык веськыд параллельнӧй визьӧс вундӧма коймӧд, сэк ӧтыдждаӧсь: 1) пытшкӧс крестӧнкуйлысь пельӧсъяс, 2) ортсыс крестӧнкуйлысь пельӧсъяс, 3) соответственнӧй пельӧсъяс да 4) кыдз пытшкӧс, сідзи и ортсыс ӧтарбокса пельӧсъяслӧн сумма 2d ыджда.

Докажитам теоремалысь 1-а юкӧн.

Сетӧма: AB ∥ CD; EF — вундысь (94 серп.).

__________________________________

Колӧ докажитны: ∠1 = ∠2.

Докажитӧм (паныдсянь). Шуам, мый ∠1 да ∠2 абу ӧтыдждаӧсь, та дырйи мед ∠1 > ∠2. M чутӧ EF вундысь бердӧ вӧчам ∠KMN = ∠1. ∠KMN да ∠MND кӧ ӧтыдждаӧсь, KM ∥ CD; та ногӧн лоӧ, мый M чут пыр мунӧны кык веськыд — KM да AB, CD-кӧд параллельнӧйяс; тайӧ паныдасьӧ параллельнӧйяс йылысь аксиомалы; та вӧсна миян шуӧмным, мый ∠1 > ∠2, оз туй.

Шуам кӧ, мый ∠1 < ∠2, M чутӧ да EF вундысь бердӧ ∠1 ыджда пельӧс вӧчӧм бӧрын бара воам сэтчӧ, мый M чут пыр мунӧны кык веськыд, CD-кӧд параллельнӧйяс, — а татшӧмторйыс оз вермы лоны сы вӧсна, мый тайӧ паныдасьӧ параллельнӧйяс йылысь аксиомалы. Та ногӧн, ∠1 кӧ оз вермы лоны ∠2-ысь ыджыдджыкӧн ни ичӧтджыкӧн, ∠1-лы колӧ ∠2-кӧд лоны ӧтыдждаӧн. Тайӧ лоӧ, мый пытшкӧс крестӧнкуйлысь пельӧсъясыс ӧтыдждаӧсь, кодъяс артмӧмаӧсь кык веськыд параллельнӧйӧс коймӧд веськыдӧн вундігӧн.

Теоремаса мукӧд юкӧнъяслӧн веськыдлуныс петӧ докажитӧмысь сы вӧсна, мый, кор пытшкӧс крестӧнкуйлысь пельӧсъяс ӧтыдждаӧсь, сэк ӧтыдждаӧсь 1) ортсыс крестӧнкуйлысь пельӧсъяс, 2) соответственнӧй пельӧсъяс да 3) кыдз пытшкӧс, сідзи и ортсыс ӧтарбокса пельӧсъяслӧн сумма 2d ыджда.

3. Следствийӧ. Кутшӧмкӧ веськыд визь кӧ перпендикуляр кык веськыд параллельнӧй пиысь ӧтиыслы, лоӧ сідзжӧ перпендикулярӧн мӧдыслы.

Сетӧма: AB ∥ CD; EF ⊥ AB (95 серп.).

_____________________________

Колӧ докажитны: EF ⊥ CD.

Докажитӧм. AB да CD кӧ параллельнӧйӧсь, ∠1 = ∠2 кыдз соответственнӧй пельӧсъяс; но ∠1 = d, сідзкӧ и ∠2 = d, кытысь EF ⊥ CD.

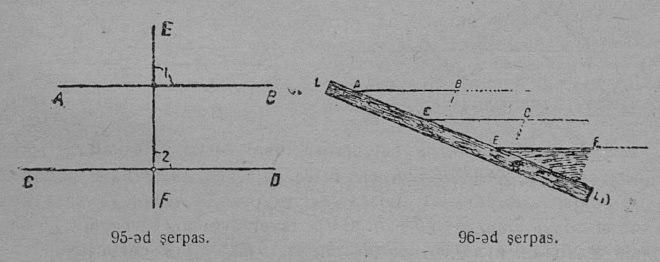
5 §. Линейка да чертёжнӧй куимпельӧса отсӧгӧн веськыд параллельнӧйясӧс вӧчӧм.

Медкокни способӧн веськыд параллельнӧй визьясӧс нуӧдавны кужӧм кутӧ ыджыд коланлун чертёжнӧй уджъяс вӧчалігӧн. Медкокни способӧн татшӧм построенньӧ вӧчсьӧ линейка да чертёжнӧй куимпельӧса отсӧгӧн да подуласьӧ кык параллельнӧй веськыдӧс коймӧдӧн вундігӧн артман соответственнӧй пельӧсъяс равенствоӧн (96 серп.).

6 §. Соответственнӧ параллельнӧй бокъяса пельӧсъяслӧн свойство.

Теорема. Соответственнӧ параллельнӧй бокъяса пельӧсъяс ӧтыдждаӧсь, кор кыкнаныс ёсьӧсь либӧ тшӧтшыдӧсь; либӧ суммаын сетӧны 2d, кор ӧтиыс ёсь, а мӧдыс — тшӧтшыд.

Сетӧма: ∠B — ёсь; MN ∥ AB да KL ∥ BC (97-ӧд серпас).

_____________________________________________

Колӧ докажитны:

1) ∠B ӧтыджда P чутса любӧй ёсь пельӧскӧд.

2) ∠B + P чутса любӧй тшӧтшыд пельӧс = 2d.

Докажитӧм. 1) P чутса пельӧслысь нюжӧдам кутшӧмкӧ ӧти бок, шуам, MN, BC боккӧд вомӧнасьтӧдз, сэк ∠B = ∠3, кыдз AB да MN параллельнӧйяс да BC вундысь бердса соответственнӧй пельӧсъяс; но ∠4 = ∠3, кыдз BC да KL параллельнӧйяс да MN вундысь бердса соответственнӧй пельӧсъяс. Та ногӧн, ∠B да ∠4 торйӧн ∠3-кӧд ӧтыдждаӧсь, сідзкӧ найӧ асьныс ӧтыдждаӧсь: ∠B = ∠4. Но ∠4 = ∠6 кыдз противоположнӧйяс; сідзкӧ, ∠B = ∠6. Та ногӧн ∠B = ∠4 = ∠6; став тайӧ пельӧсъяс — ёсьӧсь; сідзкӧ ёсь ∠B ӧтыджда P чут бердса любӧй ёсь пельӧскӧд, кодлӧн бокъясыс ∠B бокъяскӧд параллельнӧйӧсь.

2) Докажитам, мый P чут бердса любӧй тшӧтшыд пельӧскӧд ∠B суммаын сетӧ 2d. ∠4 + ∠7 = 2d, кыдз орчча пельӧсъяс, ∠4 = ∠B кыдз параллельнӧй бокъяса ёсь пельӧсъяс. Воддза равенствоысь ∠4 вежам ∠B-ӧн, сыкӧд ӧтыдждаӧн, лоӧ ∠B + ∠7 = 2d. Бӧръя равенствоын ∠7 вежам ∠5-ӧн, сылы ӧтыдждаӧн, лоӧ ∠B + ∠5 = 2d. Аддзам, мый P чутса любӧй тшӧтшыд пельӧскӧд ∠B суммаын сетӧ 2d.

7 §. Куимпельӧсаын пельӧсъяслӧн свойствояс.

Теорема. Любӧй куимпельӧсаын пытшкӧс пельӧсъяслӧн суммаыс 2d ыджда.

Сетӧма: ∆ABC (98-ӧд серпас).

______________________________

Колӧ докажитны: ∠A + ∠B + ∠C = 2d.

Докажитӧм. ABC куимпельӧсалысь AB бок нюжӧдам да B йыв пыр нуӧдам веськыдӧс — BE ∥ AC.

B чут бердса пельӧсъяслӧн сумма 2d ыджда: ∠1 + ∠2 + ∠3 = 2d.

Такӧд ӧттшӧтш построенньӧ серти лоӧ: 1) ∠1 = ∠A, кыдз соответственнӧйяс; 2) ∠2 = ∠C, кыдз крестӧнкуйлысь пельӧсъяс; 3) ∠3 = ∠B.

Но ∠1 + ∠2 + ∠3 = 2d, сідзкӧ, ∠A + ∠B + ∠C = 2d.

Следствийӧяс. 1. Куимпельӧсаын оз вермы лоны ӧти веськыд пельӧсысь либӧ ӧти тшӧтшыд пельӧсысь унджык.

Тайӧ сы вӧсна, мый куимпельӧсаын куимнан пельӧслӧн суммаыс 2d ыджда. Ӧти пельӧс кӧ на костын d ыджда либӧ d-ысь ыджыдджык, мукӧд кыклӧн сумма лоӧ d ыджда либӧ d-ысь ичӧтджык, сідзкӧ мукӧд кык пиысь ӧти пельӧс лоӧ d-ысь ичӧтджык.

2. Веськыдпельӧса куимпельӧсаын ёсь пельӧсъяслӧн суммаыс d ыджда.

3. Ӧти куимпельӧсалӧн кӧ кык пельӧс ӧтыдждаӧсь мӧд куимпельӧсаса кык пельӧскӧд, налӧн коймӧд пельӧсъясыс ӧтыдждаӧсь.

4. Куимпельӧсалӧн ортсыс пельӧсыс кык пытшкӧс пельӧсъяс сумма ыджда, кодъяс сыкӧд абу орччаӧсь,

да сідзкӧ,

5. Ортсыс пельӧс ыджыдджык быд пытшкӧс пельӧсысь, коді сыкӧд абу орчча.

Тайӧ сы вӧсна, мый

∠A + ∠B + ∠C = 2d.

∠CBD + ∠B = 2d.

___________________________________

сідзкӧ,

∠CBD = ∠A + ∠C, кытысь ∠CBD > ∠A; ∠CBD > ∠C.

6. Куимпельӧсаса ортсыс пельӧсъяслӧн сумма 4d ыджда.

Тайӧ петӧ сыысь, мый куимпельӧсаса быд йыв бердса ортсыс да пытшкӧс пельӧслӧн сумма 2d ыджда; сідзкӧ, став ортсыс да пытшкӧс пельӧсъяслӧн суммаыс 6d ыджда; а сы вӧсна, мый сӧмын пытшкӧс пельӧсъяслӧн суммаыс 2d ыджда, став ортсыс пельӧсъяслӧн сумма вылӧ колӧ 4d, 6d − 2d = 4d.

8§. Соответственнӧя перпендикулярнӧй бокъяса пельӧсъяслӧн свойство.

Теорема. Соответственнӧ перпендикулярнӧй бокъяса пельӧсъяс ӧтыдждаӧсь, кор кыкнаныс ёсьӧсь либӧ тшӧтшыдӧсь; либӧ суммаын сетӧны 2d, кор ӧтиыс — ёсь, а мӧдыс — тшӧтшыд.

Сетӧма: ∠B — ёсь; MN ⊥ AB да KL ⊥ BC (99-ӧд серпас).

_______________________________________________

Колӧ докажитны:

1) ∠B ӧтыджда P чутса любӧй ёсь пельӧскӧд;

2) ∠B + P чутса любӧй тшӧтшыд пельӧс = 2d.

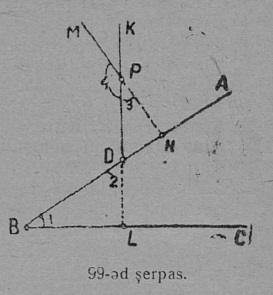
Докажитӧм. 1) Видзӧдлам веськыдпельӧса BDL да PDN куимпельӧсаяс; налӧн ∠B + ∠2 = d да ∠3 + ∠2 = d; тайӧ равенствояс ӧтластитӧмысь петӧ, мый ∠B = ∠3, коді P чут бердын. Тайӧ пельӧсъяс ёсьӧсь да ӧтыдждаӧсь.

Ас выннаныд видлалӧй сэтшӧм случайяс, кор P пельӧслӧн йыв куйлӧ 1) сетӧм B пельӧс пытшкын, 2) B пельӧс сайын сідз, мый сылӧн бокъяс вундӧны сетӧм B пельӧсса бокъяслысь нюжӧдӧмнысӧ.

2) Медым докажитны, мый ёсь ∠B да P чутса любӧй тшӧтшыд пельӧс суммаын сетӧны 2d, видзӧдлам P чут бердса 3 да 4 пельӧсъяс. ∠3 + ∠4 = 2d, но ∠3 = ∠B; первой равенствоысь ∠3-ӧс сыкӧд ӧтыджда B пельӧсӧн вежӧм бӧрын лоӧ: ∠B + ∠4 = 2d; лоӧ, мый сетӧм ёсь ∠B да P чутса тшӧтшыд пельӧс, кодлӧн бокъясыс ∠B бокъяскӧд перпендикулярнӧйӧсь, суммаын сетӧны 2d.

9 §. Параллельнӧй веськыдъясӧн вундӧм параллельнӧй веськыд вундӧгъяслӧн свойство.

1. Теорема. Параллельнӧй веськыдъясӧн вундӧм кык параллельнӧй веськыдъяслӧн вундӧгъясыс ӧтыдждаӧсь.

Сетӧма: MN ∥ M₁N₁ да KL ∥ K₁L₁ (100-ӧд серпас).

_______________________________________

Колӧ докажитны: AB = CD да AC = BD.

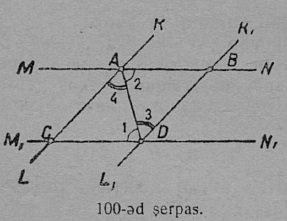
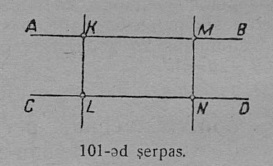
Докажитӧм. Веськыд визьӧн ӧтлаалам A да D чутъяс да видзӧдлам ABD да ACD куимпельӧсаяс. Найӧ ӧтыдждаӧсь сы вӧсна, мый налӧн 1) AD — ӧтувъя бок, 2) ∠1 = ∠2, кыдз крестӧнкуйлысь пельӧсъяс, 3) ∠3 = ∠4, кыдз крестӧнкуйлысь пельӧсъяс.

Куимпельӧсаяс равенствоысь петӧ соответственнӧй бокъяслӧн равенство, та кузя: 1) AB = CD, кыдз ӧтыджда 3 да 4 пельӧсъяс водзын куйлысь бокъяс, 2) AC = BD, кыдз ӧтыджда 1 да 2 пельӧсъяс водзын куйлысь бокъяс.

2. Кузьтаыс перпендикулярлӧн, кодӧс нуӧдӧма ӧти параллельнӧй веськыд визь вывса кутшӧмкӧ чутсянь мӧд параллельнӧй веськыд визь вылӧ, определяйтӧ асьнас кык параллельнӧй веськыд костса ылнакостсӧ.

Следствийӧ. Параллельнӧй веськыд визьяс став кузяногныс мӧда-мӧдсянь ӧтыллаынӧсь.

Сетӧма: AB ∥ CD (101-ӧд серпас).

___________________________

Колӧ докажитны: KL = MN.

Докажитӧм. KL да MN перпендикуляръяс, кодъясӧс нуӧдӧма веськыд AB визь вывса произвольнӧй K да M чутъяссянь CD веськыд визь вылӧ, параллельнӧйӧсь, KL ∥ MN. KL кӧ ∥ MN, найӧ лоӧны параллельнӧй вундӧгъясӧн AB да CD параллельнӧй веськыдъяс костын, сідзкӧ найӧ ӧтыдждаӧсь: KL = MN.

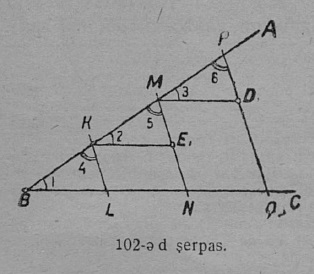
3. Теорема. Куимпельӧсаса ӧти бок вылӧ кӧ йывсянь пуктавны ӧтыджда вундӧгъяс да найӧ помъяс пырыс нуӧдны веськыд параллельнӧйясӧс пельӧсса мӧд боккӧд вундыссьытӧдз, тайӧ мӧд бок вылын артмӧны мӧда-мӧдкӧд ӧтыджда вундӧгъяс.

ABC куимпельӧсаса BA бок вылӧ пукталам ӧтыджда вундӧгъяс: BK = KM = MP (102-ӧд серпас) да нуӧдам K, M, P чутъяс пыр веськыд параллельнӧйясӧс: KL ∥ MN ∥ PQ.

Сетӧма: BK = KM = MP; KL ∥ MN ∥ PQ.

______________________________

Колӧ докажитны: BL = LN = NQ.

Докажитӧм. K да M чутъяс пыр нуӧдам веськыдъясӧс: KE ∥ BC да MD ∥ BC, да видзӧдлам артмӧм BKL, KME да MPD куимпельӧсаяс. Найӧ ӧтыдждаӧсь бок да сы бердын куйлысь 2 пельӧс серти сы вӧсна, мый BK = KM = MP построенньӧ серти, ∠1 = ∠2 = ∠3 да ∠4 = ∠5 = ∠6, кыдз соответственнӧй пельӧсъяс.

Куимпельӧсаяс равенствоысь петӧ бокъяслӧн равенство, кыдз ӧтыджда 4, 5 да 6 пельӧсъяс водзын куйлысьяслӧн; та вӧсна BL = KE = MD. Но сы вӧсна, мый 1) KE = LN да MD = NQ, кыдз параллельнӧйяс костын параллельнӧйяслӧн вундӧгъяс, да 2) докажитлӧмысь KE = MD = BL, лоӧ LN = NQ = BL.

10 §. Ӧтыджда юкӧнъясӧ вундӧгӧс юкӧм.

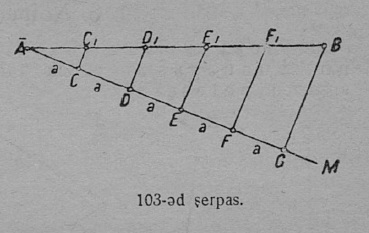
Циркуль да линейка отсӧгӧн ми вермам юкны вундӧгӧс 2, 4, 8, 16 да с. в. ӧтыджда юкӧнӧ. Видзӧдлам, кыдзи позьӧ вундӧгӧс юклыны ӧтыджда юкӧнъяса любӧй лыд вылӧ, шуам, 3, 4, 5, 6, 7 да с. в. юкӧн вылӧ.

Задача. AB вундӧгӧс юкны 5 ӧтыджда юкӧнӧ (103-ӧд серпас).

Построенньӧ. AB вундӧгса A пом пыр нуӧдам произвольнӧй пельӧсӧн отсасьысь AM веськыд визь да A йывсянь кузяногыс витысь пуктам произвольнӧй кузьтаа вундӧг: AC = a; AC = CD = DE = EF = FG = a. Медбӧръя вундӧглысь G пом ӧтлаалам сетӧм AB вундӧгса B помкӧд да юкан C, D, E, F чутъяс пыр нуӧдам BG-лы параллельнӧй веськыд визьясӧс, кодъяс AB вундӧгӧс юксясны 5 ӧтыджда юкӧнӧ: AC₁ = C₁D₁ = D₁E₁ = E₁F₁ = F₁B.

Построенньӧлысь веськыдлунсӧ докажитӧм мунӧ воддза теорема серти.

Юасянъяс да упражненньӧяс:

1. Кутшӧм вывод позьӧ вӧчны татшӧм гижӧд подувтас вылын: плоскосьт вылын сетӧма: AB ⊥ MN да CD ⊥ MN? Вӧчны чертёж.

2. Сетӧма, мый AB ⊥ KL да AB ∥ CD. Кутшӧм вывод позьӧ вӧчны сы йылысь, кыдзи мӧда-мӧдкӧд куйлӧны плоскосьт вылын индӧм визьяс? Ӧтвет вӧчны чертёжӧн.

3. Артавны кык веськыд параллельнӧй визьясӧн да найӧс вундысьӧн артман став пельӧсъяслысь ыдждаяссӧ, кор: 1) пельӧсъяс пиысь ӧтиыс куим пӧв ыджыдджык сійӧ пельӧсысь, коді сыкӧд абу^Гашкӧ, “абу” оз ков? — А.В./^ орчча; 2) пельӧсъяс пиысь ӧти 22°30’-ӧн мӧдысь ичӧтджык; 3) пельӧсъяс пиысь ӧтиыс 0,8 мӧд ыджда; 4) кык орчча пельӧсъяслӧн разносьт 37° ыджда.

4. Сетӧма: AB ∥ CD да EF — вундысь. Докажитны, мый 1) AB да CD бердса ӧтыджда пельӧсъяслӧн биссектрисаяс параллельнӧйӧсь,^Колӧ, медым пельӧсъясыс эз вӧвны веськыдъясӧн. — А.В./^ 2) AB да CD бердса пельӧсъяслӧн, кодъяс абу ӧтыдждаӧсь, биссектрисаяс перпендикулярнӧйӧсь.

5. Докажитны, мый веськыдпельӧса куимпельӧсаын 30° пельӧс водзын куйлысь бокыс гипотенуза джын ыджда.

6. Веськыдпельӧса куимпельӧсаын нуӧдны ёсь пельӧсъясын биссектрисаяс да докажитны, мый биссектрисаяс костса пельӧсыс 135° ыджда.

7. Куимпельӧсаысь тӧдмавны ортсыс да сыкӧд орчча пытшкӧс пельӧсъяслысь ыдждаяссӧ, тӧдам кӧ, мый найӧ мӧда-мӧдкӧд относитчӧны, кыдз 3 : 2; 4 : 5; 11 : 7; 5 : 13 да гижны, ыджыд-ӧ мукӧд кык пытшкӧс пельӧсъяслӧн суммаыс.

8. Артавны куимпельӧсаса пельӧсъяслысь ыджда, кор тӧдам, мый на костса отношенньӧыс, кыдз 1 : 2 : 3. Индыны, вермасны-ӧ куимпельӧсалӧн бокъясыс относитчыны, кыдз 1 : 2 : 3.

VIII. НЁЛЬПЕЛЬӦСАЯС ДА УНАПЕЛЬӦСАЯС.

1 §. Нёльпельӧсаяс.

1. Плоскосьтлӧн юкӧн, кодӧс ограничитӧма нёль вундӧгысь артмӧм тупкӧса чегсьӧм визьӧн, шусьӧ нёльпельӧсаӧн.

Нёльпельӧсаса став бокъяслӧн сумма шусьӧ нёльпельӧсаса периметрӧн. Нёльпельӧсаясӧс торйӧдӧны: выпуклӧйӧс (104-ӧд серпас) да невыпуклӧйӧс (105-ӧд серпас).

Водзӧ ми кутам видлавны сӧмын выпуклӧй нёльпельӧсаясӧс.

Выпуклӧй нёльпельӧсаӧн шусьӧ сэтшӧм, кодлӧн быд пытшкӧс пельӧс павтыртӧм пельӧсысь, 2d-ысь, ичӧтджык. Выпуклӧй унапельӧса век куйлӧ унапельӧсаса любӧй боксянь ӧтарбокын.

2. Теорема. Нёльпельӧсаса пытшкӧс пельӧсъяслӧн суммаыс 4d ыджда.

Сетӧма: нёльпельӧса ABCD (106-ӧд серпас).

_____________________________________

Колӧ докажитны: ∠A + ∠B + ∠C + ∠D = 4d.

Докажитӧм. Нуӧдам BD диагональ, нёльпельӧсаӧс сійӧ торйӧдас кык куимпельӧсаӧ. Быд куимпельӧсаын пытшкӧс пельӧсъяслӧн суммаыс 2d ыджда, сідзкӧ, кыкнан куимпельӧсаын, либӧ ABCD нёльпельӧсаын пытшкӧс пельӧсъяслӧн суммаыс лоӧ 2d∙2 = 4d.

Гижӧд:

1) ∆ABD-ын ∠A + ∠1 +∠ 4 = 2d;

2) ∆BCD-ын ∠2 + ∠C + ∠3 = 2d.

___________________________

∠A + (∠1 + ∠2) + ∠C + (∠3 + ∠4) = 4d,

либӧ ∠A + ∠B + ∠C + ∠D = 4d.

3. Теорема. Нёльпельӧсаса ортсыс пельӧсъяслӧн суммаыс 4d ыджда.

Тайӧ сы вӧсна, мый нёльпельӧсаса быд йыв бердса ортсыс да пытшкӧс пельӧсъяслӧн суммаыс 2d ыджда; сідзкӧ, нёльпельӧсаса став пытшкӧс да ортсыс пельӧсъяслӧн суммаыс лоӧ 8d; нёльпельӧсаса пытшкӧс пельӧсъяслӧн сумма 4d; та вӧсна ортсыс пельӧсъяслӧн сумма лоӧ 8d − 4d = 4d.

Любӧй нёльпельӧсаса ортсыс пельӧсъяслӧн, кыдзи и пытшкӧс пельӧсъяслӧн, сумма 4d ыджда.

4. Нёльпельӧсаяс пиысь ас формананыс, коді зависитӧ воча-воча куйлысь бокъяс положенньӧысь, торйӧдчӧ кык сикас нёльпельӧса: трапеция да параллелограмм.

Трапеция — сэтшӧм нёльпельӧса, кодлӧн кык воча куйлысь бокъясыс параллельнӧйӧсь.

Нёльпельӧса ABCD — трапеция (107-ӧд серпас).

Параллелограмм — сэтшӧм нёльпельӧса, кодлӧн воча куйлысь бокъясыс гозйӧн-гозйӧн параллельнӧйӧсь. Сійӧ артмӧ, кор кутшӧмкӧ кык параллельнӧй KL да MN веськыдъясӧс вомӧналӧны мӧд кык параллельнӧй EF да JH веськыдъяс.

ABCD нёльпельӧса — параллелограмм (108-ӧд серпас).

2 §. Параллелограмм да сылӧн свойствояс.

1. Параллелограммлӧн подувтас да судта. Параллелограммын подувтас пыдди босьтӧны кутшӧмкӧ параллельнӧй бокъяс, шуам, ABCD параллелограммын (109-ӧд серпас) AB да CD; на костса ылнакостыс, коді муртассьӧ перпендикулярӧн, шусьӧ параллелограммлӧн судтаӧн; судтаӧс унджыкысьсӧ нуӧдӧны параллелограммса кутшӧмкӧ ӧти йыв пыр; DE да DF — ABCD параллелограммлӧн кык торъя судтаяс.

2. Параллелограммса бокъяслӧн свойство.

Теорема. Параллелограммлӧн воча куйлысь бокъясыс гозйӧн-гозйӧн ӧтыдждаӧсь.

Сетӧма: ABCD — параллелограмм; AB ∥ DC, AD ∥ BC.

______________________________________

Колӧ докажитны: AB = DC; AD = BC.

Тайӧ теоремалӧн веськыдлуныс петӧ теоремаысь: параллельнӧй визьторъяс костын параллельнӧйяслӧн вундӧгъясыс ӧтыдждаӧсь.

3. Параллелограммса пельӧсъяслӧн свойство.

Теорема. Параллелограммын воча пельӧсъяс ӧтыдждаӧсь, а ӧти бок бердса пельӧсъяслӧн сумма 2d ыджда, м. л. найӧ — пополнительнӧй пельӧсъяс.

Сетӧма: ABCD — параллелограмм, AB ∥ CD, AD ∥ BC.

________________________________________

Колӧ докажитны:

1) ∠A = ∠C да ∠B = ∠D;

2) ∠A + ∠B = 2d, ∠A + ∠D = 2d да с. в.

Тайӧ сужденньӧяслӧн веськыдлуныс петӧ соответственнӧ параллельнӧй бокъяса пельӧсъяс свойство йылысь теоремаысь.

Следствийӧ. Параллелограммса пельӧсъяс пиын ӧти кӧ веськыд, сэк сылӧн став пельӧсыс веськыд.

Параллелограммса пельӧсъяс тайӧ свойствояс серти позьӧ тӧдмавны сылысь став пельӧс ыдждасӧ, кор ми тӧдам сӧмын ӧти пельӧслысь ыдждасӧ.

4. Параллелограммса диагональяслӧн свойство.

Теорема. Диагональ параллелограммӧс юкӧ кык ӧтыджда куимпельӧсаӧ.

Сетӧма:

ABCD — параллелограмм; AC диагональ

(110-ӧд серпас)

_________________________________

Колӧ докажитны: ∆ABC = ∆ACD.

Докажитӧм. ABC да ACD куимпельӧсаясын эм куим соответственнӧ ӧтыджда бокъяс: AB = DC да AD = BC, кыдз параллелограммлӧн воча бокъяс, а диагональ AC — налӧн ӧтувъя бок, та вӧсна ∆ABC = ∆ACD.

Теорема. Параллелограммын диагональяс мӧда-мӧдкӧд вомӧнасян чутын юксьӧны шӧри.

Сетӧма:

ABCD — параллелограмм, AC да BD диагональяс.

___________________________________________

Колӧ докажитны: AO = OC; BO = OD (111-ӧд серпас).

Докажитӧм. Видлалам AOB да DOC куимпельӧсаяс; AB = DC, кыдз параллелограммлӧн воча доръяс, ∠1 = ∠2 да ∠3 = ∠4, кыдз пытшкӧс крестӧнкуйлысь пельӧсъяс. Сідзкӧ, куимпельӧсаясыс ӧти бок да сы бердса ӧтыджда пельӧсъяс серти ӧтыдждаӧсь: ∆AOB = ∆DOC; куимпельӧсаяс равенствоысь петӧ соответственнӧй элементъяслӧн равенство, та вӧсна AO = OC, кыдз бокъяс, кодъяс куйлӧны ӧтыджда куимпельӧсаясын ӧтыджда пельӧсъяс ∠3 да ∠4 водзын; OD = BO, кыдз бокъяс, кодъяс куйлӧны ӧтыджда пельӧсъяс ∠1 да ∠2 водзын.

3 §. Параллелограммъяслӧн признакъяс.

1. Теорема. Нёльпельӧсаын кӧ кык воча бокъяс ӧтыдждаӧсь да параллельнӧйӧсь, сэтшӧм нёльпельӧсаыс эм параллелограмм, мӧд ногӧн, сэтшӧм нёльпельӧсалӧн тшӧтш и мӧд кык бокыс параллельнӧйӧсь.

Сетӧма:

ABCD — нёльпельӧса; AB = DC; AB ∥ DC (112-ӧд серпас).

_____________________________________

Колӧ докажитны: AD ∥ BC.

Докажитӧм. Нуӧдам AC диагональ да видлалам ∆ABC да ∆ACD. Тайӧ куимпельӧсаясын: 1) AC — ӧтвуъя бок; 2) AB = DC — условийӧ серти, 3) ∠1 = ∠2; та вӧсна ∆ABC = ∆ACD; куимпельӧсаяс равенствоысь петӧ, мый ∠3 = ∠4; тайӧ пельӧсъясыс AD да BC веськыдъяс бердса да AC вундысь бердса пытшкӧс крестӧнкуйлысь пельӧсъяс, та вӧсна AD ∥ BC.

2. Теорема. Нёльпельӧсаын кӧ воча бокъясыс гозйӧн-гозйӧн ӧтыдждаӧсь, сэтшӧм нёльпельӧсаыс эм параллелограмм, мӧд ногӧн, сэтшӧм нёльпельӧсалӧн бокъясыс гозйӧн-гозйӧн параллельнӧйӧсь.

Сетӧма:

ABCD — нёльпельӧса; AB = DC; AD = BC (112-ӧд серпас).

__________________________________________

Колӧ докажитны: AB ∥ DC; AD ∥ BC.

Докажитӧм. Нуӧдам AC диагональ да видлалам ∆ABC да ∆ACD; найӧ ӧтыдждаӧсь: налӧн AC — ӧтувъя бок, AB = CD да AD = BC. Куимпельӧсаяс равенствоысь петӧ соответственнӧя куйлысь пельӧсъяслӧн равенство: ∠1 = ∠2; тайӧ пытшкӧс крестӧнкуйлысь пельӧсъяс; та вӧсна AB ∥ DC; таысь ӧтдор, ∠3 = ∠4, та вӧсна AD ∥ BC.

Сідзкӧ, AD ∥ BC, AB ∥ CD, мӧд ног кӧ, ABCD нёльпельӧсаын воча бокъясыс гозйӧн-гозйӧн параллельнӧйӧсь; сідзкӧ, татшӧм нёльпельӧсаыс — параллелограмм.

3. Теорема. Нёльпельӧсаын кӧ диагональяс мода-мӧдӧн юксьӧны шӧри, сэтшӧм нёльпельӧсаыс эм параллелограмм, мӧд ногӧн, сэтшӧм нёльпельӧсалӧн воча бокъясыс гозйӧн-гозйӧн параллельнӧйӧсь (111-ӧд серпас).

Сетӧма:

ABCD — нёльпельӧса; AC да BD — диагональяс;

AO = OC да BO = OD.

_________________________________________

Колӧ докажитны:

AD ∥ BC да AB ∥ CD, м. л. ABCD — параллелограмм.

Докажитӧм. Видлалам AOB да DOC куимпельӧсаяс, кодъясӧ пырӧны диагональяслӧн AO да OC, BO да OD вундӧгъяс да AB да DC бокъяс. Тайӧ куимпельӧсаясын: AO = OC да BO = OD условийӧ серти да ∠α = ∠β, кыдз противоположнӧй пельӧсъяс; сідзкӧ, ∆AOB = ∆DOC; куимпельӧсаяс равенствоысь петӧ ӧтыджда бокъяс водзын куйлысь пельӧсъяслӧн равенство: ∠1 = ∠2, ∠3 = ∠4; тайӧ пельӧсъяс — крестӧнкуйлысь пельӧсъяс; та вӧсна AB ∥ DC. AOD да COB куимпельӧсаясӧс видлалӧмысь аддзам, мый найӧ ӧтыдждаӧсь, мый вӧсна петас AD ∥ CB.

Тадз, AD ∥ BC, AB ∥ CD — ABCD нёльпельӧсалӧн воча доръяс гозйӧн-гозйӧн параллельнӧйӧсь; ABCD — параллелограмм.

Индӧм признак серти вӧчӧны параллелограмм, кор сетӧма сылысь кык m да n диагональяс да на костса пельӧс — ∠α. Тайӧ свойствоӧн пӧльзуйтчӧмӧн вӧчӧны параллелограммӧс циркульӧн да линейкаӧн, — оз ковмы нуӧдавны параллельнӧй визьяс.

4 §. Параллелограммӧс вӧчӧм.

1 задача. Вӧчны параллелограммӧс диагональыс серти, коді m = 10 см да бокъясыс серти, кодъяс a = 6 см да b = 7 см.

Построенньӧ. Вӧчны куимпельӧсаӧс a, b да m бокъяс серти, сэсся тыртны сійӧс параллелограммӧдз.

2 задача. Вӧчны параллелограммӧс бокъяс серти, кодъяс a = 5 см да b = 4 см, да ∠C = 40° серти.

Построенньӧ. Водзын вӧчны куимпельӧсаӧс кык бок a да b серти да на костса C пельӧс серти, сэсся тыртны параллелограммӧдз.

3 задача. Вӧчны параллелограммӧс кык диагональыс серти, кодъяс m = 6 см да n = 10 см, да на костса пельӧс серти, коді α = 50°.

Построенньӧ. Нуӧдам (113-ӧд серпас) 50° пельӧсӧн вомӧнасян кык веськыд визь MN да EF да вомӧнасян O чутсяньныс ӧтарӧ-мӧдарӧ кыкнаныс вылӧ пукталам вундӧгъяс, кодъяс соответственнӧ равнӧйӧсь сетӧм диагональяс джынъяслы, сэсся артмӧм вундӧгъяслысь помъяссӧ ӧтлаалам: артмӧм ABCD нёльпельӧсаыс — параллелограмм.

4 задача. Вӧчны параллелограммӧс m да n диагональяс да a бок серти.

Построенньӧ. Задача решитӧм могысь колӧ построитны куимпельӧсаӧс куим бокыс серти: a, m/2 да n/2.

Задача решитӧм вермас лоны, кор a < m/2 + n/2, либӧ 2a < m + n.^Колӧ нӧшта: m/2 < a + n/2, n/2 < a + m/2. — А.В./^

5 задача. Вӧчны параллелограмм сійӧ R диагональыс серти (кодлысь сетӧма кузьтасӧ да нырвизьсӧ) да параллелограммлысь бокъяссӧ индысь P да Q нырвизьяс серти (114-ӧд серпас).

Построенньӧ. Сетӧм кузьтаа да нырвизя AB = R диагональ A пом пыр нуӧдам веськыд визьяс, кодъяс параллельнӧйӧсь индӧм бокъяс нырвизьяслы. Сэсся диагональса мӧд пом пыр — B чут пыр бара нуӧдам веськыдъясӧс, кодъяс параллельнӧйӧсь тайӧ жӧ индӧм бокъяс нырвизьяслы. Нуӧдӧм веськыд визьяслӧн вомӧнасянінса чутъяс сетасны параллелограммлысь мӧд кык йыв.

2. Тайӧяс лоӧны параллелограммӧс вӧчӧмлӧн основнӧй случайяс. Кутшӧм куимпельӧсаяс вылӧ параллелограммӧс юклӧны ӧти либӧ кыкнан диагональыс, сэтшӧм ӧти куимпельӧсаӧс построитӧмӧн определяйтчӧ ставнас параллелограммыс.

Татысь петӧны параллелограммъяс равенство йылысь со кутшӧм признакъяс.

Параллелограммъяс ӧтыдждаӧсь, кор налӧн ӧтыдждаӧсь элементъяс:

1) кык орчча бок да на костса пельӧс,

2) кыкнан диагональ да на костса пельӧс,

3) кык орчча бок да диагональ,

4) кыкнан диагональ да бок.

Оз ков вунӧдны, мый параллелограммлысь пельӧсъяс корсигӧн тырмымӧн тӧдны сӧмын ӧти пельӧслысь ыдждасӧ.

3. Задача. ABCD дзиръя параллелограммӧн исследуйтны (115-ӧд серп.), кыдз параллелограммлӧн вежласьӧны DP судта да периметр, кор сылӧн вежласьӧ кутшӧмкӧ ӧти пельӧс, шуам, A.

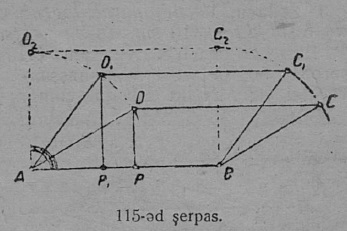
Исследованньӧ. Кор параллелограммлӧн A пельӧс вежсьӧ, DP судта сідзжӧ вежсьӧ, — та дырйи судтаыс ыдждӧ, кор ∠A содӧ 90°-ӧдз да ичӧтмӧ, кор ∠A чинӧ 0°-ӧдз; кор ∠A = 0°, параллелограмм абу, сылӧн бокъясыс вевсяасьӧны да параллелограмм пӧрӧ веськыд визьӧ, кодлӧн кузьтаыс параллелограммса кык орчча бокъяс сумма ыджда.

Кор ∠A = 90°, параллелограммлӧн став пельӧс веськыдӧсь, а DP судта лоӧ медыджыд. Став тайӧ случайясын периметр оз вежлась, век кольӧ пыр ӧткодьӧн.

5 §. Центральнӧй симметрия.

1 задача. ABCD параллелограммын (116 серп.) диагональяс вомӧнасянін O чут пыр нуӧдӧма произвольнӧй веськыд визь, коді кык параллельнӧй бокъясӧс вундӧ M да N чутъясын. Докажитны, мый MN вундӧг O чутын юксьӧ шӧри.

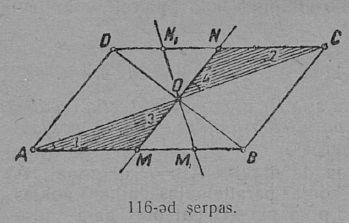
Решитӧм. AOM да ONC куимпельӧсаяс ӧтыдждаӧсь: налӧн AO = OC, ∠1 = ∠2, кыдз крестӧнкуйлысьяс, да ∠3 = ∠4, кыдз противоположнӧйяс; куимпельӧсаяс равенствоысь петӧ, мый OM = ON.

Сідзкӧ, параллелограммса диагональяслӧн вомӧнасянін O чут пыр мунысь любӧй веськыд визьлӧн вундӧг, коді йӧртчӧ параллелограммса кык бок костӧ, тайӧ O чутын юксьӧ шӧри.

2. ABCD параллелограммын (117 серп.) нуӧдам AC да BD диагональяс; найӧ вомӧнасьӧны O чутын; та дырйи артмӧ 4 куимпельӧса. На пиысь ӧтиӧс, шуам, ∆AOB, бергӧдам серпас плоскосьтын O чут гӧгӧр 180° вылӧ, сэк B йыв усьӧ D йылӧ (OB = OD) да A йыв усьӧ C йылӧ (OA = OC); куимпельӧсаяслӧн став 3 йыв вевсяасисны, сідзкӧ, вевсяасясны асьныс куимпельӧсаяс. Тадз жӧ лоӧ BOC да DOA, ABC да CDA куимпельӧсаяскӧд да MBCN да NDAM нёльпельӧсаякӧд (116 серпас).

3. Кык чут A да C, B да D, кык вундӧг AB да CD, BC да DA, AO да OC, OB да OD, кык фигура ∆AOB да ∆COD, ∆ABC да ∆CDA шусьӧны O чут серти центрально-симметричнӧйясӧн, кор чут гӧгӧрыс 180° вылӧ бергӧдігӧн ӧтиыс кӧ вевсяасяс мӧдыс вылӧ.

Фигура шусьӧ центрально-симметричнӧйӧн, кор сетӧм O чут гӧгӧр 180° вылӧ сійӧс бергӧдігӧн сылӧн быд юкӧн босьтас сэтшӧм места, кодӧс вӧлі босьтӧ фигуралӧн мӧд юкӧн. O чутыс, код гӧгӧр фигураӧс бергӧдӧны 180° вылӧ, шусьӧ симметрия шӧрчутӧн.

4. Параллелограмм — центрально-симметричнӧй фигура, кӧн симметрия шӧрчутыс параллелограммса диагональяс вомӧнасянін чутын.

5. Параллелограммлӧн симметрия осьяс абу.^Сійӧ кӧ абу веськыднёльпельӧса либӧ ромб. — А. В. /^

6 §. Куимпельӧсалӧн шӧр визь.

Вундӧг, кодлӧн помъясыс куимпельӧсаса кык бок шӧрын, шусьӧ куимпельӧсаса шӧр визьӧн.

Теорема. Куимпельӧсалӧн шӧр визьыс параллельнӧй коймӧд боклы да сы джын ыджда.

Сетӧма:

ABC — куимпельӧса; AE = EC, BD = DC (118 серп.).

_____________________________________

Колӧ докажитны: ED ∥ AB да ED = ½AB.

Докажитӧм. ED нюжӧдӧм вылӧ пуктам ED ыджда DF вундӧг да F чут ӧтлаалам B чуткӧд. Артмас ∆CED-кӧд ӧтыджда ∆BDF сы вӧсна, мый CD = BD, ED = DF да ∠1 = ∠2. Куимпельӧсаяс равенствоысь петӧ, мый ∠3 = ∠4, та вӧсна BF ∥ EC, BF ∥ AC; таысь ӧтдор, BF = EC = AE, сідзкӧ, ABFE нёльпельӧсаыс лоӧ параллелограмм сы вӧсна, мый воча BF да AE бокъяс ӧтыдждаӧсь дай параллельнӧйӧсь. Та ногӧн, EF ∥ AB да EF = AB, но EF = ED + DF = 2ED = AB, та вӧсна ED = ½AB.

7 §. Веськыднёльпельӧса. Сылӧн свойствояс.

1. Нуӧдам кӧ KL да MN веськыд параллельнӧйясӧс да найӧс вундам веськыд пельӧс улын мӧд кык EF да NQ веськыд параллельнӧйясӧн (119-ӧд серпас), веськыд параллельнӧйяс костса вундӧгъяс вӧчасны веськыдпельӧса ABCD параллелограмм; татшӧм параллелограмм шусьӧ веськыднёльпельӧсаӧн.

Сідзкӧ, веськыднёльпельӧса эм веськыдпельӧса параллелограмм.

Веськыднёльпельӧса, коді ӧттшӧтш лоӧ параллелограммӧн, кутӧ сылысь став свойствояссӧ:

Веськыднёльпельӧсаын: 1) воча бокъяс ӧтыдждаӧсь; 2) воча пельӧсъяс ӧтыдждаӧсь да на пиысь быд пельӧс веськыд пельӧс ыджда; 3) диагональ сійӧс торйӧдӧ кык ӧтыджда веськыдпельӧса куимпельӧсаӧ; 4) диагональяс мӧда-мӧдӧн юксьӧны шӧри; 5) диагональяс вомӧнасянін чутыс лоӧ сылӧн симметрия шӧрчут.

Веськыднёльпельӧсалӧн кутшӧмкӧ ӧти бок шусьӧ сійӧ подувтасӧн; подувтаскӧд орчча бокыс шусьӧ сійӧ судтаӧн.

2. Теорема. Веськыднёльпельӧсалӧн диагональяс мӧда-мӧдкӧд ӧтыдждаӧсь.

Докажитӧм. ∆ABD да ∆ACD (120-ӧд серпас) — веськыдпельӧсаяс да ӧтыдждаӧсь кык соответственнӧ ӧтыджда катетъяс серти: AD — ӧтувъя катет да AB = CD, кыдз веськыднёльпельӧсалӧн воча бокъяс. Куимпельӧсаяс равенствоысь петӧ, мый AC = BD: веськыднёльпельӧсалӧн диагональяс ӧтыдждаӧсь.

Пӧлӧс пельӧса параллелограммын тайӧ абу: сылӧн диагональяс абу ӧтыдждаӧсь; параллелограммса ёсь пельӧсъяслысь йывъяс ӧтлаалысь диагональ ыджыдджык сійӧ диагональысь, коді ӧтлаалӧ тшӧтшыд пельӧсъяслысь йывъяс.

8 §. Веськыднёльпельӧсаӧс вӧчӧм.

Параллелограмм вӧчӧм вылӧ колӧ тӧдны сылысь куим элемент.

Веськыднёльпельӧсаӧс вӧчӧм вылӧ, коді эм веськыдпельӧсъяса параллелограмм, колӧ тӧдны сӧмын кык линейнӧй элемент; веськыднёльпельӧсалысь индавны коймӧд элементсӧ — орчча бокъяс костса пельӧссӧ — нинӧмла: веськыднёльпельӧсаын быд пельӧс веськыд.

Веськыднёльпельӧсаӧс позьӧ вӧчны, кор сетӧма:

1) кык орчча бок a да b, 2) диагональ m да кодыскӧ ӧти бок, 3) кодыскӧ ӧти бок, a либӧ b, да пельӧс, коді артмӧ диагональӧн да сетӧм бокӧн, 4) диагональ m да диагональяс костса пельӧс α.

Задача. Вӧчны веськыднёльпельӧсаӧс диагональ m = 8 см да диагональяс костса ∠ α = 30° пельӧс серти.

Построенньӧ. MN да KL кык веськыдӧс вомӧналам 30° улын. Вомӧнасянін O чутсянь на кузя ӧт-мӧдарӧ пуктам вундӧгъяс, m/2 = 8/2 = 4 см ыдждаясӧс, сэсся вундӧгъяслысь помъяссӧ ӧтлаалам веськыд визьясӧн.

Та ногӧн артман нёльпельӧсаыс — веськыднёльпельӧса.

9 §. Веськыднёльпельӧсаын симметрия осьяс.

ABCD веськыднёльпельӧсаса AC да BD диагональяслӧн вундысянін O чут пыр кӧ нуӧдны бокъяслы перпендикулярнӧй KL да MN веськыд визьяс (121 серп.) да сэсся код веськыдӧдыс кӧ, KL-ӧд либӧ MN-ӧд, кусыньтны серпас, серпаслӧн ӧти юкӧн ставнасӧн ӧтлаасяс мӧд юкӧнкӧд. Сідзкӧ:

1) KL да MN веськыдъяс, кодъяс веськыднёльпельӧсаса бокъяскӧд перпендикулярнӧйӧсь да мунӧны диагональяс вомӧнасянін чут пыр, лоӧны веськыднёльпельӧсаса симметрия осьясӧн;

2) веськыднёльпельӧсаын симметриялӧн кык ось.

Веськыднёльпельӧсаса симметрия ось свойствоысь петӧ, мый ось юкӧ воча бокъяссӧ шӧри; вундӧг, коді ӧтлаалӧ веськыднёльпельӧсаса воча бокъяслысь шӧръяс, шусьӧ веськыднёльпельӧсаса шӧр визьӧн; сійӧ ӧтыджда веськыднёльпельӧсаса параллельнӧй боккӧд.

10 §. Ромб да сылӧн свойствояс.

1. Параллелограмм, кодлӧн став бокъясыс ӧтыдждаӧсь, шусьӧ ромбӧн.

Ромб — ӧткузя бокъяса параллелограмм.

Ромбӧс урчитӧмысь петӧ (122 серп.):

1) AB ∥ CD да AD ∥ BC;

2) AB = BC = CD = AD.

2. Ромблӧн свойствояс. Ромб, кыдз ӧткузя бокъяса параллелограмм, кутӧ сылысь став свойствояс.

Ромбын: 1) воча пельӧсъяс ӧтыдждаӧсь, та дырйи найӧ кыкнаныс либӧ ёсьӧсь либӧ тшӧтшыдӧсь; 2) ӧти любӧй бок бердса пельӧсъяс мӧда-мӧдлы пополнительнӧйӧсь: суммаын сетӧны 2d; 3) диагональ юкӧ сійӧс кык ӧтыджда (кык ӧткузя бока) куимпельӧсаӧ; 4) диагональяс мӧда-мӧдӧн вундыссьӧны шӧри; 5) диагональяслӧн вомӧнасянін чутыс — сылӧн симметрия шӧрчут.

3. Теорема. Ромблӧн диагональяс: 1) мӧда-мӧдкӧд перпендикулярнӧйӧсь; 2) сылысь пельӧсъяс юкӧны шӧри; 3) лоӧны сылӧн симметрия осьясӧн; 4) торйӧдӧны сійӧс 4 ӧтыджда веськыдпельӧса куимпельӧсаӧ.

Сетӧма:

ABCD — ромб; AC да BD — сылӧн диагональяс (123 серп.).

______________________________________________

Колӧ докажитны: 1) AC ⊥ BD; 2) ∠1 = ∠2; ∠3 = ∠4;

3) AC да BD — симметрия осьяс;

4) ∆AOB = ∆BOC = ∆COD = ∆DOA.

Докажитӧм. Видлалам ∆ABD; сійӧ — кык ӧткузя бока: условийӧ серти AB = AD; татысь петӧ, мый ромблӧн AC диагональ, коді тайӧ куимпельӧсаті мунӧ BD бок шӧр пыр, лоӧ ADB куимпельӧсаын медианаӧн, ∠A-лӧн биссектрисаӧн, куимпельӧсалӧн судтаӧн, симметрия осьӧн да ∆ABD торйӧдӧ кык ӧтыджда веськыдпельӧса AOB да AOD куимпельӧсаясӧ.

Сідзкӧ, 1) AC ⊥ BD; 2) ∠1 = ∠2; 3) AC — ромбын симметриялӧн ось; ∆AOB = ∆AOD.

Кык ӧткузя бока ADC куимпельӧсаӧс, кӧн AD = DC да DO мунӧ AC бок шӧр пыр, видлалӧмысь петӧ, мый 1) OD ⊥ AC; 2) ∠3 = ∠4; 3) DB — ромбын симметриялӧн ось; 4) ∆AOD = ∆DOC.

Куимпельӧсаяс AOB да AOD, AOD да COD, COD да BOC равенствоысь петӧ, мый ∆AOB = ∆AOD = ∆COD = ∆BOC.

4. Ромбӧс вӧчигӧн используйтӧны диагональяслысь свойство, кодъяс мӧда-мӧдӧн юксьӧны шӧри да мӧда-мӧдкӧд перпендикулярнӧйӧсь.

11 §. Ромбӧс вӧчӧм.

1 задача. Вӧчны ромб a бок да ∠A серти.

Построенньӧ. Вӧчам ∠A да сійӧ йывсянь кыкнан бок кузя пуктам ӧтыджда вундӧгъяс: AB = AD = a. B да D помъяс ӧтлаалам да артман ABD куимпельӧсаӧс тыртам ромбӧдз.

2 задача. Вӧчны ромб, кодлӧн диагональяс m да n.

Построенньӧ. Нуӧдам мӧда-мӧдкӧд перпендикулярнӧй кык веськыд MN да KL визьяс (124 серп.). Налысь вомӧнасянін O чут босьтам ромбса диагональяс мӧда-мӧдкӧд вундысянін чут пыдди. O чутсянь кыкнан визь кузя ӧтарӧ и мӧдарӧ пуктам гозйӧн-гозйӧн ӧтыджда вундӧгъяс: KL кузя OB = OD = m/2 да MN кузя OA = OC = n/2. Сэсся вундӧгъяслысь помъяс ӧтлаалам; артман ABCD нёльпельӧсаыс лоӧ ромб.

2. Ромб вӧчӧм вылӧ колӧ тӧдны сылысь сӧмын кык элемент: 1) бок да пельӧс, 2) кык диагональ, 3) бок да диагональ, 4) диагональ да пельӧс.

12 §. Квадрат да сылӧн свойствояс.

Сэтшӧм веськыднёльпельӧса, кодлӧн кык орчча бокъяс ӧтыдждаӧсь, шусьӧ квадратӧн (125^126?/^ серп.).

Веськыднёльпельӧсаын воча бокъяс ӧтыдждаӧсь; квадратын воча бокъяс да орчча бокъяс ӧтыдждаӧсь:

AB = BC = CD = AD.

Сідзкӧ, квадрат эм ӧткузя бокъяса веськыднёльпельӧса.

Сэтшӧм ромб, кодлӧн ӧти пельӧсыс веськыд, шусьӧ квадратӧн (125^126?/^ серп.).

Ромбын воча пельӧсъяс ӧтыдждаӧсь; квадратын воча пельӧсъяс ӧтыдждаӧсь да веськыдӧсь:

∠A = ∠B = ∠C = ∠D = d.

Сідзкӧ, квадрат эм ӧтыджда пельӧсъяса ромб.

Квадрат обладайтӧ веськыднёльпельӧсаса да ромбса став свойствоясӧн.

Квадратын (126^125?/^ серп.): 1) диагональяс мӧда-мӧдӧн юксьӧны шӧри, 2) диагональяс мӧда-мӧдкӧд ӧтыдждаӧсь, 3) шӧр визь — симметриялӧн ось, 4) диагональяс мӧда-мӧдкӧд перпендикулярнӧйӧсь, 5) диагональяс сылысь пельӧсъяс юкӧны шӧри, 6) диагональяс — симметриялӧн осьяс, 7) симметриялӧн нёль ось: AC, BD, MN да KL.

13 §. Квадратӧс вӧчӧм.

1 задача. Вӧчны a = 2,5 см бока квадрат (127 серп.).

Построенньӧ. Вӧчам веськыд пельӧс. Сы бокъяс кузя йывсянь пуктам a = 2,5 см вундӧгъяс; кыкнан вундӧг помъяссянь гижтам a = 2,5 см радиусъясӧн дугаяс; налысь вомӧнасянін чут ӧтлаалам вундӧгъяс помъяскӧд. Артман нёльпельӧсаыс лоӧ — квадрат.

Квадрат вӧчӧм вылӧ колӧ тӧдны сӧмын сійӧ дорлысь кузьта.

2 задача. Вӧчны квадрат m = 6 см диагональ серти.

Построенньӧ. Нуӧдам кык веськыд визь MN да KL сідз, мед найӧ вомӧнасясны O чутын веськыд пельӧс улын. O чутсянь кыкнан визь кузя ӧтарӧ и мӧдарӧ пуктам ӧтыджда вундӧгъяс: m/2 = 3 см. Вундӧгъяслысь помъяс ӧтлаалам да лоӧ нёльпельӧса — квадрат.

Квадрат вӧчӧм вылӧ колӧ тӧдны сӧмын сійӧ диагональлысь кузьта.

14 §. Трапеция.

1. ABCD нёльпельӧса, кодлӧн кык воча бокъяс параллельнӧйӧсь, шусьӧ трапецияӧн.

2. Трапециялӧн параллельнӧй бокъяс шусьӧны подувтасъясӧн, а мукӧд кык AD да CB доръяс — трапеция боквывса бокъясӧн.

3. Трапеция, кодлӧн боквывса бокъясыс ӧтыдждаӧсь, шусьӧ кык ӧткузя бока трапецияӧн (128 серп.): AB ∥ DC да AD = BC.

4. Трапеция, кодлӧн ӧти пельӧс веськыд, шусьӧ веськыдпельӧсаӧн (129 серп.): AB ∥ DC да CB ⊥ AB.

5. Трапецияын кык подувтас костса меддженьыд расстоянньӧ определяйтчӧ перпендикуляр кузьтаӧн, кодӧс нуӧдӧма ӧти подувтасса кутшӧмкӧ чутсянь мӧд подувтас вылӧ. Тайӧ перпендикуляр ӧттшӧтш лоӧ трапециялӧн судта (130 серп.). AA₁, DD₁, KK₁, CC₁ ӧтыдждаӧсь, кыдз параллельнӧйяслӧн вундӧгъяс параллельнӧй визьяс костын: AA₁ = DD₁ = KK₁ = CC₁.

15 §. Кык ӧткузя бока трапециялӧн свойствояс.

1. Теорема. Кык ӧткузя бока трапецияын кутшӧмкӧ ӧти подувтас бердса пельӧсъяс ӧтыдждаӧсь.

Сетӧма: ABCD — трапеция; AD = BC (128 серп.).

_________________________________

Колӧ докажитны: ∠A = ∠B да ∠C = ∠D.

Докажитӧм. Нуӧдам CF ∥ AD; артмӧ ∆CFB; сійӧ — кык ӧткузя бока сы вӧсна, мый AD = CF = CB; сідзкӧ ∠2 = ∠3, кыдз кык ӧткузя бока куимпельӧсаын подувтас бердса пельӧсъяс. Но ∠2 = ∠1, кыдз AD да CF параллельнӧйяс бердса соответственнӧй пельӧсъяс, та вӧсна ∠1 = ∠3.

2. Веськыдпельӧса ABCD трапецияын кӧ (131 серп.), кӧн CB ⊥ AB, CB босьтны симметрия ось пыдди да вӧчны сылы симметричнӧй CBA₁D₁ трапеция, татшӧм построенньӧӧн артмӧм AA₁D₁D фигура лоӧ кык ӧткузя бока трапецияӧн. Тайӧ трапецияын B да C чутъяс куйлӧны AA₁ да DD₁ подувтасъясса шӧръясын; тайӧ чутъясӧс ӧтлаалысь CB веськыд визь кык ӧткузя бока AA₁D₁D трапецияын лоӧ симметрия осьӧн.

Кык ӧткузя бока трапециялӧн эм ӧти симметрия ось; сійӧ мунӧ подувтасъясса шӧръяс пыр да накӧд перпендикулярнӧй; кык ӧткузя бока трапецияса параллельнӧй бокъяслӧн шӧр визь лоӧ симметрия осьӧн.

16 §. Трапецияса боквывса бокъяслӧн шӧр визь.

1. Трапециялӧн шӧр визь эм вундӧг, кодлӧн помъясыс трапецияса боквывса бокъяс шӧрын.

ABCD трапецияын (132 серп.) M чут AD боклӧн шӧр, N чут BC боклӧн шӧр; AM = MD да BN = NC; MN — трапециялӧн шӧр визь.

2. Теорема. Трапециялӧн шӧр визь подувтасъяскӧд параллельнӧй да найӧ сумма джын ыджда.

Сетӧма: ABCD — трапеция; MN — шӧр визь (132 серп.).

____________________________________

Колӧ докажитны: MN ∥ AB ∥ DC; 2) MN = (AB + DC)/2.

Докажитӧм. 1) Нюжӧдам DC бок да CB бок шӧрса N чут пыр нуӧдам веськыд EF ∥ AD; артмасны кык куимпельӧса: ∆CNE да ∆FNB, налӧн 1) CN = NB условийӧ серти, 2) ∠1 = ∠2, кыдз противоположнӧйяс, ∠3 = ∠4, кыдз параллельнӧйяс бердса пельӧсъяс, сідзкӧ, ∆CNE = ∆FNB.

Куимпельӧсаяс равенствоысь петӧ, мый CE = FB да EN = NF, либӧ EN = EF/2, но EF вундӧг AD ыджда да сыкӧд параллельнӧй, та вӧсна EN = AD/2 = MD. Сідзкӧ, EN = MD да EN ∥ MD; сідзкӧ, MDEN нёльпельӧсаыс лоӧ параллелограмм, кысь петӧ, мый DE ∥ MN.

Трапецияын DC ∥ AB да докажитӧм серти DC ∥ MN, та вӧсна MN ∥ AB. Сідзкӧ, MN ∥ AB ∥ DC. Теоремалысь 1-а юкӧн лои докажитӧма.

2) Видзӧдлам AMNF да DMNE параллелограммъяс вылӧ; налӧн

MN = AF = AB − FB

MN = DE = DC + CE

________________

2MN = AF + DE = AB + DC − FB + CE,

но FB = CE, та вӧсна 2MN = AB + DC, либӧ MN = (AB + DC)/2.

Пасйӧд. Трапециялӧн шӧр визьыс кыкнан подувтасса средньӧй арифметическӧй ыджда. Сідз, трапециялӧн кӧ бокъясыс: a = 14 см да b = 8 см, трапециялӧн шӧр визьыс: m = (a + b)/2 = (14 + 8)/2 = 11 см.

17 §. Трапецияӧс вӧчӧм.

1. Трапеция определяйтчӧ 4 элементӧн, кодъяс костӧ вермӧны пырны подувтас бердса ӧти пельӧс либӧ кыкнаныс:

1) ас нёльнан бокнас,

2) кык подувтасӧн, боквывса ӧти бокӧн да пельӧсъяс пиысь ӧтиӧн,

3) кык подувтасӧн, боквывса ӧти бокӧн да диагональӧн,

4) кык подувтасӧн, боквывса ӧти бокӧн да судтаӧн,

5) подувтасӧн, сы бердса кык пельӧсӧн да судтаӧн.

2. Сы вӧсна, мый кык ӧткузя бока трапецияын ӧтыдждаӧсь боквывса бокъяс да подувтас бердса пельӧсъяс, а веськыдпельӧсаын — кык пельӧс веськыдӧсь, найӧс вӧчӧм вылӧ индӧм элементъяс пиысь колӧ сӧмын куим, кодъяс костӧ вермӧ пырны ӧти пельӧс.

3. Задача. Вӧчны трапеция сы нёль бок серти: a, b, c да d; a да b — подувтасъяс, c да d — боквывса бокъяс (133 да 134 серп.).

Построенньӧ. Шуам, мый ABCD трапецияӧс вӧчӧма нин (134 серп.). Вуджӧдам AD бок аскӧдыс параллельнӧя CE положенньӧӧ, сэк трапеция торйӧдчас ADCE параллелограммӧ да BCE куимпельӧсаӧ, кодъясӧс вӧчны ми кужам сы вӧсна, мый найӧс вӧчӧм вылӧ эмӧсь став колана сетӧмъяс: куимпельӧса вӧчӧм вылӧ — сылӧн став бокъяс: CE = c, CB = d, BE = a − b; параллелограмм вӧчӧм вылӧ — AD = c, AE = b да ∠AEC.

Татшӧм исследованньӧ бӧрын вӧчам построенньӧ. Задачаын сетӧмъяс серти вӧчам ∆BCE, нюжӧдам BE да сы вылӧ пуктам вундӧг BA = a; A чутысь нуӧдам AD ∥ CE, а C чутысь нуӧдам CD ∥ AB да артмас корсян трапеция ABCD. Задача артмас, кор c − d < a − b < c + d.^Кор c < d, колӧ d − c < a − b < c + d. — А. В./^

18 §. Нёльпельӧсаӧс определяйтысь элементъяслӧн лыд.

1. Сетӧм куим элемент серти кӧ позьӧ вӧчны помтӧм уна куимпельӧса, кодъяс ӧтыдждаӧсь мӧда-мӧдкӧд да мӧда-мӧдысь янсӧдчӧны сӧмын положенньӧнаныс, но оз янсӧдчыны ни форманас, ни размеръяснас, найӧ ставныс лоӧны ӧти сійӧ жӧ куимпельӧсалӧн копияяс. Татшӧм случайын шуӧны, мый позьӧ вӧчны сӧмын ӧти куимпельӧсаӧс, определённӧй формаа да определённӧй размера куимпельӧсаӧс. Тӧдана, мый татшӧм куимпельӧсалысь позьӧ босьтны помтӧм уна копия.

Сідз, куимпельӧсаӧс позьӧ вӧчны, кор сетӧма сылысь со кутшӧм основнӧй куим элемент:

1) ӧти бок да сы бердса кык пельӧс (кодъяслӧн суммаыс 2d-ысь ичӧтджык);

2) кык бок да на костса пельӧс (180°-ысь ичӧтджык);

3) куим бок (кодъяс пиысь медыджыдыс кык мукӧд суммаысь ичӧтджык).

Основнӧй кык элемент серти определённӧй размера куимпельӧсаӧс вӧчны он вермы. Сідз, шуам, сетӧм кык бок серти, либӧ бок да пельӧс серти позьӧ вӧчны помтӧм уна куимпельӧсаӧс, кодъяс кутасны мӧда-мӧдысь торйӧдчыны формананыс дай размеръяснаныс; а кык пельӧс серти позьӧ вӧчны помтӧм уна куимпельӧса, кодъяс кутасны мӧда-мӧдысь торйӧдчыны размеръяснаныс. Мед шуам, сетӧма ABC куимпельӧса (135 серп.). AC боквывса кутшӧмкӧ E чут пыр кӧ нуӧдны EF веськыдӧс, AB подувтаслы параллельнӧйӧс, артмас ∆CEF, кодлӧн пельӧсъяс лоӧны ABC куимпельӧсаса пельӧсъяс ыджда: C пельӧс — ӧтувъя, ∠E = ∠A да ∠F = ∠B кыдз соответственнӧйяс; тыдалӧ, мый тайӧ куимпельӧсаяс абу ӧтыдждаӧсь, найӧ мӧда-мӧдысь торйӧдчӧны размеръясӧн, кӧть налӧн пельӧсъяс ӧтыдждаӧсь. Та ногӧн, куим пельӧс серти определённӧй размера куимпельӧса вӧчны он вермы. Куимпельӧсалӧн пельӧсъяс костын эм определённӧй соотношенньӧ: ∠A + ∠B + ∠C = 2d = 180°, та вӧсна куимпельӧсалысь пельӧсъяс определитӧм вылӧ колӧ тӧдны сылысь кык пельӧс сы вӧсна, мый коймӧд пельӧс наӧн определяйтчӧ нин, пример вылӧ: ∠C = 180° − (∠A + ∠B). Татысь петӧ, мый сетӧма кӧ куим пельӧс, кодъяслӧн сумма 180° ыджда, тайӧ условийӧын сӧмын кык независимӧй элемент — кык пельӧс, сы вӧсна мый коймӧд наӧн определяйтчӧ.

Куимпельӧсаӧс позьӧ вӧчны куим независимӧй элемент серти.

Но вермас лоны и сідз, кыдз ми аддзам водзысьджык, мый и куим независимӧй элементъяс серти позьӧ вӧчны не ӧтикӧс, а кыкӧс различнӧй формааӧс дай размераӧс. Сетӧм куим элемент пиӧ кӧ пырӧны неосновнӧйяс, вермас артмыны помтӧм уна различнӧй формаа да размера куимпельӧсаяс.

Та вӧсна сы бӧрын, кор куимпельӧсаӧс лоӧ вӧчӧма, колӧ исследуйтны, кымын решитӧм, ӧтик либӧ некымын, задачаса условийӧын сетӧм элементъяс серти вермас лоны, да кутшӧм сетӧмъяс дырйи задача оз вермы решитчыны — оз вермы лоны построенньӧ.

2. Параллелограммъяс вӧчӧм, кыдз тӧдам, вайӧдчӧ куимпельӧсаяс вӧчӧмӧ; та вӧсна параллелограмм вӧчӧм вылӧ колӧ тӧдны сылысь сӧмын куим независимӧй элемент.

3. Веськыднёльпельӧса вӧчӧм вылӧ колӧ тӧдны сылысь сӧмын кык линейнӧй элемент; сетны коймӧд элемент — сылысь пельӧс — нинӧмла сы вӧсна, мый веськыднёльпельӧсаын став пельӧсыс веськыдӧсь.

4. Ромб вӧчӧм вылӧ сідзжӧ колӧ сӧмын сылӧн кык независимӧй элемент.

5. Квадрат вӧчӧм вылӧ колӧ тӧдны сылысь сӧмын ӧти линейнӧй элемент: бок либӧ диагональ.

6. Трапеция вӧчӧм вылӧ элемент лыд колӧ форма серти:

1) кык ӧткузя бока трапеция вӧчӧм вылӧ — 3 элемент,

2) веськыдпельӧса трапеция вӧчӧм вылӧ — 3 элемент,

3) ӧтувъя трапеция (абу кык ӧткузя бока да абу веськыдпельӧса) вӧчӧм вылӧ — 4 элемент.

7. Любӧй формаа нёльпельӧса вӧчӧм вылӧ колӧ 5 независимӧй элемент.

Босьтам кӧ шарнирнӧй нёльпельӧсаӧс (136 серп.), позьӧ бокъяслысь кузьта вежлавтӧг, а на костса пельӧсъясӧс вежлалӧмӧн артмӧдны помтӧм уна различнӧй формаа нёльпельӧсаяс; сы вылӧ, мед нёльпельӧса вӧлі определённӧй формаа, колӧ сетны нӧшта сылысь витӧд элемент — либӧ пельӧсъяс пиысь ӧти пельӧс либӧ диагональяс пиысь ӧти диагональ.

Нёльпельӧсаын кӧ нуӧдны диагональяс пиысь ӧтиӧс, коді сылысь крепитас кык йыв, артмас определённӧй формаа нёльпельӧса сы вӧсна, мый сійӧ артмӧ кык куимпельӧса вӧчӧмӧн, кодъяс определяйтчӧны нёльпельӧсаса диагональӧн да бокъясӧн.

Та ногӧн, диагональ нёльпельӧсалы сетӧ чорыд форма либӧ, кыдз шуӧны, зумыд форма.

Нёльпельӧса позьӧ вӧчны кор, шуам, сетӧма сылысь со кутшӧм вит элемент: 1) 4 бок да диагональ, 2) 4 бок да пельӧс, 3) 3 бок да 2 диагональ, 4) 3 бок да 2 пельӧс, 5) 2 бок да 3 пельӧс да с. в.

8. Нёльпельӧса вежлалӧ формасӧ, кор бокъяслысь кузьта вежтӧг кутам вежлавны пельӧсъяслысь ыджда. Куимпельӧсаын мӧд нога удж. Куимпельӧсалысь бокъяслысь кузьта вежтӧг вежны форма он вермы. Тайӧ важнӧй свойство серти — не вежлавны ассьыс форма — куимпельӧса шусьӧ чорыд, либӧ зумыд фигураӧн.

Куимпельӧсалӧн индӧм свойство сетӧ зэв важнӧй значенньӧ техникаын да строительствоын.

Куимпельӧсалӧн форма используйтчӧ стропилӧяс, пос фермаяс, лэптан кранъяс да мукӧд зэв уна различнӧй предметъяс да машина детальяс вӧчалігӧн. Нёльпельӧсаыд абу зумыд фигура.

Нёльпельӧсалы мед сетны зумыд форма, вӧрзьытӧг крепитӧны сылысь кык неорчча йыв, мый вӧсна нёльпельӧса пӧрӧ кык куимпельӧсаӧ, кодъяс пиысь кыкнаныс зумыд, устойчивӧй фигураяс.

Нёльпельӧса пӧрӧ зумыд фигураӧ нӧшта сэк, кор бокъяслысь кузьта вежтӧг кык орчча бок костӧ пуктам вӧрзявтӧм угольник.

19 §. Унапельӧса. Сійӧ пельӧсъяслӧн свойство.

1. Плоскосьтлӧн юкӧн, кодӧс ограничитӧма n бока тупкӧса чегсьӧм визьӧн, шусьӧ n-пельӧсаӧн; n вермас лоны любӧй быдса лыдӧн, 3-ысь ыджыдджыкӧн либӧ тшук 3 ыдждаӧн.

Водзӧ ми кутам видлавны сӧмын выпуклӧй унапельӧсаясӧс — сэтшӧмъясӧс, кодъясын быд пытшкӧс пельӧсыс ичӧтджык 2d дорысь.

2. Теорема. n-пельӧсаын пытшкӧс пельӧсъяслӧн сумма 2d(n − 2) ыджда, либӧ 180°(n − 2) ыджда.

Докажитӧм. Унапельӧса пытшкын кӧнкӧ босьтам O чут да ӧтлаалам сійӧс став йывъяскӧд, артмасны n куимпельӧсаяс; артмас сы мында куимпельӧса, кымын бок унапельӧсаын, став n куимпельӧсаясын пытшкӧс пельӧсъяслӧн сумма 2d·n ыджда, кытчӧ пырӧны O чут бердса ӧтувъя йыла пельӧсъяс, кодъяслӧн сумма 4d ыджда. n-пельӧсаын пытшкӧс пельӧсъяслӧн сумма лоӧ n куимпельӧсаясса пытшкӧс пельӧсъяс сумма ыджда, кор сэсь шыбитан O чут гӧгӧрса пельӧсъяслысь сумма: 2dn − 4d = 2d(n − 2), либӧ 180°(n − 2). Тадз, n-пельӧсаын пытшкӧс пельӧсъяслӧн сумма 2d ыджда, кодӧс ӧктӧма кык боктӧм бокъясыс лыд вылӧ.

3. ABCDE унапельӧсаын кӧ (138 серп.) сылысь кутшӧмкӧ ӧти бок, шуам AB, нюжӧдны, тайӧ боклӧн нюжӧдӧм да сыкӧд орчча BC^серпас сертиыс, колӧ гижны AE/^ бок вӧчасны пельӧс, коді шусьӧ унапельӧсалӧн ортсыс пельӧсӧн.

ABCDE унапельӧсалысь кӧ нюжӧдны став бок, артмас сы мында ортсыс пельӧс, кымын бок либӧ пельӧс унапельӧсаын.

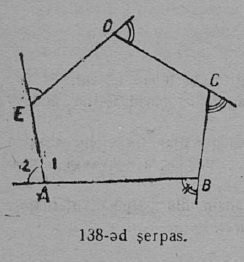
4. Теорема. Любӧй унапельӧсаын ортсыс пельӧсъяслӧн сумма 4d ыджда, либӧ 360° ыджда.

Докажитӧм. Унапельӧсаса быд йыв бердса пытшкӧс да ортсыс пельӧсъяслӧн сумма 2d ыджда; кор n йыв лоӧ 2d∙n; но n-пельӧсаын став пытшкӧс пельӧсъяслӧн сумма 2dn − 4d; сідзкӧ, мед корсьны n-пельӧсаса ортсыс пельӧсъяслысь сумма, колӧ 2dn-ысь чинтыны 2dn − 4d; лоӧ: 2dn − (2dn − 4d) = 2dn − 2dn + 4d = 4d, либӧ 360°.

Тадз, любӧй унапельӧсаын став ортсыс пельӧсъяслӧн сумма 4d ыджда. Сумма оз зависит бокъяс лыдысь.

Юасянъяс да упражненньӧяс.

1. Мый вӧсна унапельӧсаын пытшкӧс пельӧсъяслӧн сумма оз вермы лоны 7d либӧ 11d ыджда, вообще — d бердса нечётнӧй лыдлы?

2. ABCD нёльпельӧсалӧн AC диагональ = m = 6,4 см торйӧдӧ сійӧс кык куимпельӧсаӧ, кодъяс пиын ӧтилӧн периметр = 16,8 см, а мӧдлӧн = 20,2 см. Тӧдмавны ABCD нёльпельӧсалысь P периметр.

3. Тӧдмавны построенньӧӧн R равнодействующӧйлысь величина да направленньӧ P да Q кык вынлысь, кор P = 8 кг., Q = 6 кг., ∠(P, Q) = 60°.

4. Тӧдмавны построенньӧӧн составляйтысь P да Q силаяслысь направленньӧяс да величинаяс, кор тӧдам, мый R равнодействующӧй 20 кг ыджда да соответствуйтысь силаяскӧд вӧчӧ пельӧсъяс ∠(P, R) = 30° да ∠(Q, R) = 90°.

5. Вӧчны параллелограмм со кутшӧм сетӧмъяс серти: a да b — бокъяс, m да n — диагональяс:

1) a = 4,5 см, b = 3,2 см, ∠A = 40°;

2) a = 7 см, b = 5,3 см, ∠B = 110°;

3) a = 6,3 см, b = 4,7 см, m = 8 см;

4) m = 8 см, n = 6,4 см, на костын пельӧс β = 45°;

5) a = 7 см, ∠A = 130° да пельӧс α, коді артмӧма параллелограммса a бокӧн да ӧти диагональӧн, 40° ыджда.

6) a = 8 см, b = 6 см, судта h = 4 см.

6. Вӧчны веськыднёльпельӧса, кор сетӧма:

1) кык бок a = 6,4 см, b = 4,3 см;

2) бок a = 5,7 см, диагональ m = 7,5 см;

3) диагональ m = 8,4 см, диагоналя-бока костса пельӧс α = 40°;

4) диагональ m = 8 см, диагональяс костса пельӧс β = 60°;

5) бок b = 5 см, диагональяс костса пельӧс β = 110°.

7. Вӧчны ромб, кор сетӧма:

1) бок a = 4 см да пельӧс α = 40°;

2) бок a = 5 см да диагональ m = 5 см; тӧдмавны тшӧтш пельӧсъяс.

3) диагональ m = 6 см да пельӧс α = 120°;

4) диагональяс m = 5 см, n = 8 см;

5) бок a = 5 см да судта h = 3 см.

8. Вӧчны квадрат 1) бок серти a = 3,5 см; 2) диагональ серти m = 4,5 см.

9. Докажитны, мый кык ӧткузя бока трапецияын диагональяс ӧтыдждаӧсь да подувтасъяскӧд вӧчӧны ӧтыджда пельӧсъяс.

10. Докажитны, мый кык ӧткузя бока трапецияын диагональяс торйӧдӧны сійӧс 4 куимпельӧсаӧ, кодъяс пиысь подувтас бердсаяс кык ӧткузя бокаӧсь, а боквывса бокъяс бердсаяс мӧда-мӧдкӧд ӧтыдждаӧсь.

11. Кык ӧткузя бока трапецияын диагональяс мӧда-мӧдлы перпендикулярнӧйӧсь. Трапециялӧн судта 10 см ыджда. Артавны шӧр визьлысь кузьта.

IX. ВЕСЬКЫДВИЗЯ ФИГУРАЯСЛӦН ПЛОЩАДЬЯС.

1 §. Площадьясӧс мурталӧм.

1. Муртавны площадь — корсьны отношенньӧсӧ сетӧм площадьлысь мӧд площадькӧд, кодӧс босьтӧма единица пыдди. Площадь мера единица пыдди босьтӧны квадратлысь площадь, кодлӧн бокыс кутшӧмкӧ линейнӧй мера единица ыджда; пример вылӧ, миллиметр, сантиметр, метр ыджда да с. в.; татшӧм мера единица шусьӧ квадратнӧй единицаӧн.

2. Квадратнӧй единицаяс гижсьӧны тадз: 1 кв. мм, либӧ 1 мм²; 1 кв. см, либӧ 1 см², 1 кв. м, либӧ 1 м² да с. в. Площадь мера единица бӧрйӧм бӧрын, фигуралысь мурталӧны площадь: тӧдмалӧны, кымын квадратнӧй единица тӧрӧ мурталан площадьӧ.

3. Фигуралӧн площадь оз тӧдмавсьы площадь мера единицаӧн непосредственнӧя мурталӧмӧн, мӧд ног кӧ шуны, тӧдмалӧны оз единица пыдди босьтӧм площадкаясӧн сійӧс тыртӧмӧн, кыдз мыччӧдӧма 139 серпас вылын. Фигураса площадьлӧн ыджда тӧдмавсьӧ косвеннӧй мурталӧмӧн: мурталӧны фигуралысь бокъяс да мукӧд отсасьысь визьяс, кодъясӧс нуӧдалӧны фигураын, да артман лыдъяс серти арталӧны площадь.

2 §. Веськыднёльпельӧсалӧн да квадратлӧн площадь.

Теорема. Веськыднёльпельӧсалӧн площадьыс подувтаслӧн судта вылӧ произведенньӧ ыджда.

Сетӧма: ABCD — веськыднёльпельӧса (140-ӧд серпас).

AB = a — подувтас; CB = h — судта.

_______________________________

Колӧ докажитны: площадь S = a∙h.

Видзӧдлам торйӧн сэтшӧм случайяс, кор ӧти сійӧ жӧ единицаӧн мурталӧм подувтасын да судтаын: 1) быдса лыд, 2) дроба лыд.

Докажитӧм. I случай. Мед подувтас AB = a см, судта BC = h см, кӧн a да h быдса лыдъяс. Юкам AB подувтас a ыджда юкӧнӧ, 1 см-ӧн быдын, судта CB — сэтшӧм жӧ h юкӧнӧ. Юкӧм чутъяс пыр нуӧдам веськыднёльпельӧсаса бокъяслы параллельнӧйясӧс. Веськыднёльпельӧса торйӧдчас 1 см² площадя квадратъясӧ. Сы вӧсна, мый AB подувтаслы параллельнӧйяс веськыднёльпельӧсаӧс торйӧдӧны h полосаӧ, CB судталы параллельнӧйяс торйӧдӧны быд полоса 1 см² площадя a квадратӧ, став сэтшӧм квадратъяслӧн лыд лоӧ a∙h ыджда.

Сідзкӧ, ABCD веськыднёльпельӧсалӧн площадь торйӧдчӧ 1 см² площадя a∙h квадратӧ; формулаӧн тайӧ гижсяс тадз:

S = a∙h см², мӧд ног кӧ шуны,

веськыднёльпельӧсалӧн площадь сэтшӧм квадратнӧй единицаяс лыд ыджда, коді артмӧ сылысь подувтас да судта ӧти нима линейнӧй единицаясӧн мыччӧдлысь лыдъясӧс ӧктӧмысь.

II случай. Подувтас AB = a см, CD судта = h см, a да h — дроба лыдъяс. Мед тайӧ дроба лыдъяс ӧтувъя знаменательӧ вайӧдӧм бӧрын лоӧны: a = p/n да h = q/n. a да h вундӧгъяслы ӧтувъя мера пыдди босьтам 1/n см ыджда вундӧг, сэк тайӧ ӧтувъя мераыс a вундӧгӧ тӧрас p мындаысь, а h вундӧгӧ — q мындаысь; юкӧм чутъяс пыр нуӧдам веськыднёльпельӧсаса бокъяслы веськыд параллельнӧйясӧс, мый вӧсна веськыднёльпельӧсаыс юксяс 1/n см бока p∙q ичӧт квадратӧ (141-ӧд серп.); 1 см²-ын татшӧм ичӧт квадратъяслӧн лыд лоӧ n∙n = n²; сідз, квадратлысь кӧ 1 см кузя орчча бокъяс юкны 10 ӧтыджда пельӧ, квадрат торйӧдчӧ 10∙10 = 10² = 100 ичӧт квадратӧ; на пиысь быд ӧти квадрат лоӧ 1 см² площадя квадратысь 1/100 юкӧн ыджда.

Сідзкӧ, 1 см²-ын кӧ n² ичӧт квадрат, на пиысь быд ӧти квадрат лоӧ 1 см²-лӧн 1/n² юкӧн. Сетӧм веськыднёльпельӧсаын лои p∙q ичӧт квадрат, мый сетӧ p∙q/n² см², либӧ

но p/n = a да q/n = h, та вӧсна вермам гижны, мый

тайӧ петкӧдлӧ, мый веськыднёльпельӧсалӧн площадьыс — сійӧ подувтаслӧн судта вылӧ произведенньӧ ыджда. Теоремаыс лоӧ веськыд и сэки, кор веськыднёльпельӧсалысь ӧти орчча боксӧ либӧ кыкнан орчча боксӧ петкӧдлӧма иррациональнӧй лыдъясӧн.

Следствийӧяс. 1. Квадратлӧн площадь равняйтчӧ аслас бок квадратлы.

Квадрат эм веськыднёльпельӧса, кодлӧн став бокыс ӧтыджда. Квадратлысь бок пасъям a пыр, сэк сылӧн судта h = a, а та вӧсна

S = a∙a = a² кв. ед.

2. Разнӧй подувтасъяса да судтаяса кык веськыднёльпельӧсалӧн площадьяс отношенньӧ равняйтчӧ найӧ подувтасъяс да судтаяс отношенньӧясса произведенньӧлы:

S₁ = a₁h₁ да S₂ = a₂h₂,

кытысь

3. Ӧтыджда подувтасъяса кык веськыднёльпельӧсалӧн площадьяс относитчӧны, кыдз налӧн судтаяс; кор налӧн ӧтыдждаӧсь судтаяс, площадьяс относитчӧны, кыдз подувтасъяс.

4. Кык квадратлӧн площадьяс относитчӧны, кыдз найӧ бокъяслӧн квадратъяс:

S₁ = a² да S₂ = b², кытысь S₁/S₂ = a²/b².

3 §. Ӧтыдждаяс, ӧтыдждаысь тэчсьӧмъяс (равносоставленные) да ӧтгырся (равновеликие) фигураяс.

1. ABCD параллелограммын A да B йывъяссянь нуӧдам AE да BF судтаяс (142-ӧд серпас); лоӧ кык ӧтыджда веськыдпельӧса куимпельӧса ADE да BCF: гипотенуза AD = BC да катет ED = FC.

Та бӧрын кӧ ABCD параллелограммысь вундыны BFC куимпельӧсаӧс да пуктыны сійӧс параллелограммса AD бок бердӧ сідз, мед AD да BC бокъяс ӧтлаасясны, артмас ABFE веськыднёльпельӧса, коді тэчсьӧма сійӧ жӧ юкӧнъясысь, мыйысь и ABCD параллелограмм: ABFD веськыдпельӧса трапецияысь да куимпельӧсаысь.

2. Босьтам ABCD параллелограмм (143-ӧд серпас). D йывсянь BC бок шӧр пыр нуӧдам веськыд визь да нюжӧдам сійӧс AB бокӧс нюжӧдӧмкӧд F чутын вомӧнасьтӧдз; сэк лоӧ кык ӧтыджда куимпельӧса: ∆DMC да ∆BMF: налӧн MB = MC, M бердса пельӧсъяс ӧтыдждаӧсь, кыдз противоположнӧйяс, ∠B = ∠C, кыдз крестӧнкуйлысьяс.

ABCD параллелограмм да ADF куимпельӧса, кыдз аддзам, вӧчсьӧмаӧсь ӧтыджда юкӧнъясысь: ABMD трапецияысь да DMC = BMF куимпельӧсаысь.

3. Нӧшта видзӧдлам кык ӧткузя бока ABC куимпельӧсаӧс (144-ӧд серпас); CD судтаӧн сійӧ торйӧдчӧ кык ӧтыджда куимпельӧсаӧ; тайӧ куимпельӧсаяс мӧда-мӧд вылӧ пуктігӧн ӧтлаасьӧны; сідзкӧ, налӧн ӧтыджда площадьяс. Тайӧ кык куимпельӧсаысь ӧти куимпельӧсаӧс мӧд бердӧ ӧтыджда бокъяснас пукталӧмӧн позьӧ вӧчны разнӧй фигураяс, кодъяслӧн ыджданыс серти площадьяс лоӧны ӧтыдждаӧсь, а формаяс разнӧйӧсь. Пример вылӧ, ∆CBD позьӧ ∆ACD бердӧ пуктыны сідз, мый артмас либӧ ADBC параллелограмм (145-ӧд серпас), либӧ кык ӧткузя бока ABC куимпельӧса (146-ӧд серпас), либӧ ADCB нёльпельӧса (147-ӧд серпас).

Тайӧ став фигураяслӧн, кыдз ӧтыджда юкӧнъясысь тэчсьӧмъяслӧн, ӧти сійӧ жӧ площадь; та дырйи асьныс фигураясыс абу ӧтыдждаӧсь, сы вӧсна, мый мӧда-мӧд вылӧ пуктігӧн оз ӧтлаасьны.

4. 1) Ӧтыджда юкӧнъясысь тэчсьӧм фигураяс шусьӧны ӧтыдждаысь тэчсьӧмаясӧн.

2) Кык фигура, кодъяслӧн площадьяс ӧтыдждаӧсь, шусьӧны ӧтгырсяясӧн.

3) Кык ӧтыджда фигураяс ӧтгырсяӧсь.

4) Кык ӧтыдждаысь тэчсьӧм фигураяс ӧтгырсяӧсь.

5) Колӧ индыны, мый кык ӧтгырся унапельӧсаӧс век позьӧ тэчны ӧтмында да ӧтыджда юкӧнъясысь, мӧдног кӧ шуны, найӧ — ӧтыдждаысь тэчсьӧмаяс.^Тайӧ Бойяи – Гервин теорема. — А. В. /^

4 §. Параллелограммлӧн площадь.

Теорема. Параллелограммлӧн площадьыс — подувтасыслӧн судта вылӧ произведенньӧ ыджда.

Докажитӧм. Параллелограммын (148-ӧд серпас) сылысь кык судта нуӧдӧм бӧрын артмас кык веськыдпельӧса куимпельӧса ADE да BCF. Сетӧм ABCD параллелограмм да ABFE веськыднёльпельӧса — ӧтгырсяӧсь, кыдз ӧтыдждаысь тэчсьӧм фигураяс. ABFE веськыднёльпельӧсалӧн площадь = ah, сідзкӧ и ABCD параллелограммлӧн площадь = ah;

S = ah кв. ед.

Следствийӧяс. 1. Ӧтыджда подувтасъяса да судтаяса параллелограммъяс ӧтгырсяӧсь.

ABCD да A₁B₁C₁D₁ параллелограммъяслӧн (149-ӧд серпас) судтаяс да подувтасъяс ӧтыдждаӧсь: AB = A₁B₁ = a. Налӧн площадьяс S₁ = ah да S₂ = ah, сідзкӧ, S₁ = S₂ = a∙h: параллелограммъяс ӧтгырсяӧсь.

ABCD да A₁B₁C₁D₁ абу ӧтыдждаӧсь: мӧда-мӧд вылӧ пуктігӧн найӧ оз ӧтлаасьны сы вӧсна, мый налӧн ыджданыс серти пельӧсъяс разнӧйӧсь.

2. Ӧтыджда подувтасъяса параллелограммъяслӧн площадьяс относитчӧны, кыдз налӧн судтаяс; ӧтыдждаӧсь кӧ судтаяс, площадьяс относитчӧны кыдз подувтасъяс.

5 §. Куимпельӧсалӧн площадь.

1. Теорема. Куимпельӧсалӧн площадьыс — сійӧ подувтас да судта произведенньӧ джын ыджда.

Докажитӧм. Сетӧм ∆ABC (150-д серп.) содтам ABDC параллелограммӧдз BD ∥ AC да CD ∥ AB нуӧдӧмӧн. ABDC параллелограммлӧн площадь = c∙h; ∆ABC-лӧн площадь ABDC параллелограмм площадь джын ыджда; сідзкӧ ABC куимпельӧсалӧн площадьыс = ½c∙h. Тадз,

S = ½ch кв. ед.

Следствийӧяс. Веськыдпельӧса ABC куимпельӧсалысь кӧ (151-ӧд серпас) пасъям катетъяс a да b пыр, гипотенуза c пыр да гипотенуза вылӧ нуӧдӧм судта h_c пыр, веськыдпельӧса куимпельӧсалысь площадь позьӧ висьтавны кык ногӧн:

1) S = ½a∙b да 2) S = ½c∙h_c,

сідзкӧ, S = ½a∙b = ½c∙h_c, кытысь a∙b = c∙h_c.

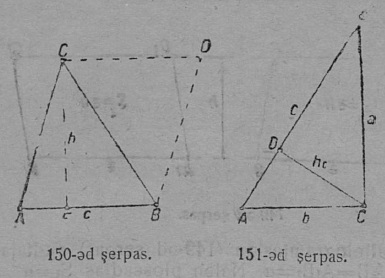
1) Веськыдпельӧса куимпельӧсалӧн площадьыс равняйтчӧ катетъясыс произведенньӧ джынлы.

2) Веськыдпельӧса куимпельӧсаса катетъяслӧн произведенньӧыс равняйтчӧ гипотенуза да сылы соответствуйтысь судта произведенньӧлы.

3) Ӧтыджда подувтасъяса куимпельӧсаяслӧн площадьяс относитчӧны, кыдз налӧн судтаяс; ӧтыдждаӧсь кӧ судтаяс, площадьяс относитчӧны, кыдз подувтасъяс.

4) Разнӧй подувтасъяса да судтаяса куимпельӧсаяс площадьяслӧн отношенньӧ равняйтчӧ найӧ подувтасъяс да судтаяс отношенньӧяс произведенньӧлы.

S₁ = ½a₁∙h₁ да S₂ = ½a₂∙h₂,

кытысь

5) Ӧтыджда судтаяса да ӧтыджда подувтасъяса куимпельӧсаяс ӧтгырсяӧсь.

Сетӧма ∆ABC. Сылысь C йыв кӧ кутам вештавны AB подувтаслы параллельнӧй веськыд визь кузя (152-ӧд серпас), а подувтас колям вежлавтӧг, лоӧ помтӧм уна куимпельӧса: ABC₁, ABC₂, ABC₃ да с. в. Быд сэтшӧм куимпельӧсалӧн площадь = ½c∙h, сідзкӧ, ставныс найӧ ӧтгырсяӧсь.

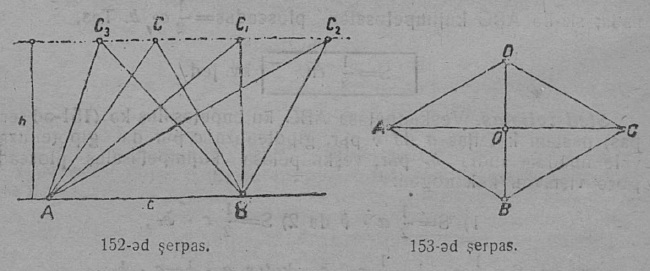
6) Ромблӧн, кыдзи и быд параллелограммлӧн, площадьыс равняйтчӧ подувтас да судта произведенньӧлы: S = a∙h. Таысь ӧтдор, ромблӧн площадь диагональяс произведенньӧ джын ыджда.

Тадзсӧ сы вӧсна, мый ABCD ромблӧн (153 серпас) AC да BD диагональяс мӧда-мӧдкӧд перпендикулярнӧйӧсь, сідзкӧ,

∆ADC-лӧн площадь = ½AC∙DO

∆ABC-лӧн площадь = ½AC∙OB

__________________________

ABCD-лӧн площадь = ½AC∙(DO + OB) = ½AC∙BD.

7) Квадратлӧн площадь равняйтчӧ ас диагональыс квадрат джынлы.

Квадратын диагональяс мӧда-мӧдкӧд перпендикулярнӧйӧсь да ӧткузяӧсь (154-ӧд серпас); сідзкӧ, ABCD квадратлӧн площадь = ½AC∙BD = ½AC².

2. Куимпельӧсалысь площадь позьӧ петкӧдлыны любӧй сійӧ бок пыр да сылы соответствуйтысь судта пыр:

S∆ = ½ah_a = ½bh_b = ½ch_c,

татысь петӧ

1) a = 2S/h_a; b = 2S/h_b; c = 2S/h_c;

2) h_a = 2S/a; h_b = 2S/b; h_c = 2S/c.

Босьтам куимпельӧсаса 1) бокъяслысь отношенньӧ да 2) судтаяслысь отношенньӧ, лоӧ:

либӧ

Дзик жӧ тадз лоӧ:

либӧ

либӧ:

куимпельӧсалӧн бокъяс мӧдара пропорциональнӧйӧсь налы соответствуйтысь судтаяслы.

3. Татшӧм жӧ соотношенньӧ бокъяс да судтаяс костын эм параллелограммын. Ромбын, кодлӧн бокъясыс ӧтыдждаӧсь да сы вӧсна налӧн отношенньӧ 1 ыджда, судтаяс ӧтыдждаӧсь.

6 §. Трапециялӧн площадь.

Теорема. Трапециялӧн площадь равняйтчӧ подувтасъяс сумма джын да судта произведенньӧлы либӧ шӧр визь да судта произведенньӧлы.

Сетӧма: ABCD — трапеция; a да b — подувтасъяс;

h — судта (155-ӧд серп.).

________________________________________

Колӧ докажитны: ABCD-лӧн пл. = S = (a + b)∙h/2.

Докажитӧм. DB диагональӧн ABCD трапеция торйӧдчӧ кык куимпельӧсаӧ: ∆ABD да ∆DBC; трапециялӧн площадьыс артмӧм куимпельӧсаяс площадьяс сумма ыджда:

ABCD пл. = ABD пл. + BDC пл. = ½ah + ½bh = ½(a + b)∙h.

S = ½(a + b)∙h = m∙h кв. ед.,

кӧн m = ½(a + b) = MN — трапециялӧн шӧр визь.

7 §. Унапельӧсалӧн площадь.

Унапельӧсалысь площадьсӧ корсьӧны куимпельӧсаясӧ да трапецияясӧ сійӧс торйӧдалӧмӧн. Первой случайын унапельӧсаса ӧти йылысь нуӧдӧны став диагональ да арталӧны артман куимпельӧсаяслысь площадьяс; став куимпельӧсаяслӧн площадь суммаыс сетӧ унапельӧсалысь площадь.

Мӧд случайын нуӧдӧны ӧти диагональ да йывъяссянь диагональ вылӧ нуӧдӧм перпендикуляръясӧн унапельӧсаӧс торйӧдлӧны веськыдпельӧса куимпельӧсаясӧ да трапецияясӧ (156-ӧд серпас). Артман куимпельӧсаяслӧн да трапецияяслӧн площадьяс сумма сетӧ унапельӧсалысь площадь.

8 §. Пифагорлӧн теорема.

Теорема. Веськыдпельӧса куимпельӧсаса гипотенуза бердӧ вӧчӧм квадратлӧн площадьыс равняйтчӧ сійӧ катетъяс бердӧ вӧчӧм квадратъяс площадьяс суммалы.

Сетӧма: ∆ABC, ∠C = d; ABNL, ACED, BCFK —

квадратъяс (157-ӧд серпас).

_________________________________________

Колӧ докажитны: ABNL пл. = ACED пл. + BCFK пл.

Первойя докажитӧм (сетіс Эвклид ас “Началаясас”). Нуӧдам CM ⊥ LN; CM-ӧн ABNL квадрат торйӧдчӧ кык веськыднёльпельӧсаӧ: APML да PBNM. Докажитам, мый на пиысь быд веськыднёльпельӧса соответственнӧ ӧтгырся квадратъяс пиысь ӧтиыскӧд, кодъясӧс вӧчӧма катетъяс бердӧ. Сідз, APML веськыднёльпельӧса ӧтгырся ACED квадраткӧд. Тайӧ вот кыдз: D ӧтлаалам B-кӧд да C ӧтлаалам L-кӧд, лоӧ кык куимпельӧса: ∆ADB да ∆ACL, кодъяс ӧтыдждаӧсь: AD = AC, AB = AL да ∠DAB = ∠CAL, кыдз веськыд пельӧсысь да ABC-са A пельӧсысь артмӧмъяс. Но ∆ABD-лӧн площадь ACED площадь джын ыджда сы вӧсна, мый сылӧн квадраткӧд AD подувтас — ӧтувъя, да BT судта квадратса DE судта ыджда. Дзик жӧ сідз ∆ACL-лӧн площадь APML площадь джын ыджда сы вӧсна, мый сылӧн веськыднёльпельӧсакӧд AL подувтас — ӧтувъя да CS судта веськыднёльпельӧсаса ML судта ыджда. ∆ABD = ∆ACL, та вӧсна ½APML пл. = ½ACED пл., либӧ APML пл. = ACED пл.: APML веськыднёльпельӧсалӧн площадь ACED квадрат площадь ыджда. Сэсся A ӧтлаалам K-кӧд да C ӧтлаалам N-кӧд да воддза моз жӧ докажитам, мый BNMP веськыднёльпельӧсалӧн площадь BCFK квадрат площадь ыджда. Тадз,

APML пл. = ACED пл. да BNMP пл. = BCFK пл.;

сідзкӧ,

APML пл. + BNMP пл. = ACED пл. + BCFK пл.,

кытысь

ABNL пл. = ACED пл. + BCFK пл.

Теорема лои докажитӧма.

Мӧд докажитӧм. Сетӧма веськыдпельӧса ABC куимпельӧса. Вӧчам построенньӧ, кыдз индӧма 158 серпас вылын, да B чут ӧтлаалам M чуткӧд. Лоӧ веськыдпельӧса CDMB трапеция, кодлӧн подувтасъяс a да b, CD судта = a + b. Тайӧ трапеция вӧчсьӧма куим веськыдпельӧса куимпельӧсаысь: 1, 2, 3.

∆1 пл. + ∆2 пл. + ∆3 пл. = CDMB пл., м. л.

ab/2 + ab/2 + c²/2 = (a + b)(a + b)/2,

либӧ

2ab + c² = a² + 2ab + b², либӧ c² = a² + b², —

гипотенузалӧн квадрат равняйтчӧ катетъяс квадратъяс суммалы.

1 задача. Вӧчны квадрат, кодлӧн площадь a да b бокъяса кык квадрат площадьяс сумма ыджда.

Решитӧм. Вӧчам веськыдпельӧса куимпельӧса, кодлӧн катетъяс a да b вундӧгъяс. Сэк Пифагор теорема серти: c² = a² + b², м. л. куимпельӧсаса c гипотенуза бердӧ вӧчӧм квадрат ӧтгырся a да b бокъяса вӧчӧм квадратъяс суммакӧд.

2 задача. Вӧчны квадрат, кодлӧн площадьыс равняйтчӧ кык сетӧм квадрат площадьяс разносьтлы.

Решитӧм. Мед сетӧм квадратъяс пиысь ыджыдджыкыслӧн бокыс = c, а ичӧтджыкыслӧн — = a; вӧчам веськыдпельӧса куимпельӧсаӧс, кодлӧн гипотенузаыс = c, а ӧти катет = a; мӧд b катет лоӧ корсян квадратлӧн бок. b вундӧг вылӧ вӧчӧм квадрат — корсян квадрат.

9 §. Веськыдвизя фигураясӧс налы ӧтгырся мӧд фигураясӧ пӧртӧм.

Кутшӧмкӧ веськыдвизя фигураӧс сылы ӧтгырся мӧд фигураӧ пӧртӧмыд лоӧ построенньӧ вылӧ задача; тайӧ задача решитӧм мунӧ фигураясса площадьяс йылысь теоремаяс серти.

1 задача. ABCD параллелограмм пӧртны сійӧ жӧ подувтаса ӧтгырся веськыднёльпельӧсаӧ (159-ӧд серпас).

Построенньӧ. a да h — ABCD параллелограммлӧн подувтас да судта; сылӧн площадь S = ah; колӧ, мед сылы ӧтгырся веськыднёльпельӧсалӧн площадь вӧлі та ыджда жӧ.

Параллелограммса a подувтас бердӧ вӧчам параллелограммса судтаа жӧ веськыднёльпельӧсаӧс, лоӧ корсян DD₁C₁C веськыднёльпельӧса; сійӧ лӧсялӧ задача условийӧлы: S = ah.

2 задача. ABCD параллелограмм пӧртны ӧтгырся куимпельӧсаӧ.

Построенньӧ. Сетӧм ABCD параллелограммлысь кутшӧмкӧ ӧти бок, шуам BC, юкам шӧри (160-ӧд серпас) да D йывсянь BC бок шӧр M чут пыр нуӧдам DF веськыдӧс AB бок нюжӧдӧмкӧд F чутын вомӧнасьтӧдз. Лоӧ ∆ADF сетӧм ABCD параллелограммлы ӧтгырся.

Збыльысь ӧд: ABCD пл. = ABMD пл. + DCM пл.; ADF пл. = ABMD пл. + BMF пл., но ∆DCM = ∆BMF: CM = BM, ∠1 = ∠2 да ∠3 = ∠4; та вӧсна ABCD пл. = ADF пл., а тайӧ лоӧ, мый ∆ADF да ABCD параллелограмм ӧтгырсяӧсь.

3 задача. ABCDE унапельӧсаӧс пӧртны сылы ӧтгырся куимпельӧсаӧ (161-ӧд серпас).

Построенньӧ. Нуӧдам AD диагональ, коді сетӧм ABCDE унапельӧсаысь вундас ∆ADE; E йыв пыр нуӧдам веськыдӧс ME ∥ AD, коді BA бок нюжӧдӧмкӧд вомӧнасяс M чутын. M чут ӧтлаалам D йывкӧд, лоӧ ∆DMA, тайӧ куимпельӧса да ∆DEA ӧтгырсяӧсь сы вӧсна, мый налӧн ӧти сійӧ жӧ подувтас да E да M йывъяс куйлӧны подувтаслы параллельнӧй веськыд визь вылын. ∆DEA вежам сыкӧд ӧтгырся DMA куимпельӧсаӧн, лоӧ MDCB унапельӧса ABCDE унапельӧсакӧд ӧтгырся, кодлӧн бок лыдыс ӧтиӧн сетӧмаысь этшаджык. Татшӧм нога построенньӧ колӧ нуӧдны сэтчӧдз, кытчӧдз сетӧм унапельӧса оз пӧр ӧтгырся куимпельӧсаӧ. Серпас вылын нуӧдӧма AD да BD диагональяс да ABCDE унапельӧса колана построенньӧясӧн пӧртӧма ӧтгырся MBP куимпельӧсаӧ.

4 задача. Сетӧм куимпельӧсаӧс юкны сійӧ йыв пыр мунысь веськыдъясӧн n мында ӧтгырся юкӧнъясӧ.

Построенньӧ. Куимпельӧсалысь подувтас юкам n мында ӧтыджда юкӧнӧ да юкан чутъяссӧ ӧтлаалам йывкӧд; артмасны n мында куимпельӧсаяс, кодъяслӧн эм ӧтыджда подувтасъяс да ӧтувъя йыв, сідзкӧ, и ӧтувъя судта, та вӧсна куимпельӧсаяс ӧтгырсяӧсь.

5 задача. Сетӧм параллелограммӧс юкны нёль ӧтгырся юкӧнӧ веськыдъясӧн, кодъяс петӧны ӧти йылысь.

Построенньӧ. DB диагональӧн ABCD параллелограмм юксьӧ кык ӧтыджда юкӧнӧ: ∆ABD = ∆BDC (162-ӧд серпас). Параллелограммса AB да BC бокъяслысь E да F шӧръяс ӧтлаалам D йывкӧд, сэк лоӧ 4 ӧтгырся куимпельӧса.

6 задача. Сетӧм параллелограммӧс юкны куим ӧтгырся юкӧнӧ веськыдъясӧн, кодъяс петӧны ӧти йылысь.

Построенньӧ. DB диагональӧн ABCD параллелограмм торйӧдчӧ кык ӧтыджда куимпельӧсаӧ (163-ӧд серпас). AB да BC бокъяс юкам 3 ӧтыджда юкӧнӧ да юкан E, F, G, H чутъяс ӧтлаалам D йывкӧд: лоӧ 6 ӧтгырся куимпельӧса: быд куимпельӧсалӧн площадь параллелограмм площадьысь 1/6 юкӧн, сідзкӧ, ADF куимпельӧсалӧн, BFDG нёльпельӧсалӧн да CDG куимпельӧсалӧн площадьяс параллелограмм площадьысь 1/3 ыдждаӧсь.

7 задача. Куимпельӧсаса бок вылын босьтӧм любӧй чут пыр нуӧдны веськыд визь сідз, мед сійӧ куимпельӧсаӧс юкас кык ӧтгырся юкӧнӧ.

Построенньӧ. ABC куимпельӧсаса AB бок вылын сетӧма произвольнӧй K чут (164 серп.). K чут ӧтлаалам C йывкӧд да C йывсянь нуӧдам CM медиана. CM медиана куимпельӧсаӧс юкӧ кык ӧтгырся куимпельӧсаясӧ: CMA да CMB. Нуӧдам MD ∥ CK да D чут ӧтлаалам K чуткӧд; артмасны кык ӧтгырся куимпельӧса: ∆CMD да ∆DMK, сы вӧсна, мый налӧн MD — ӧтувъя подувтас да налӧн C да K йывъяс куйлӧны DM веськыдлы CK параллельнӧй вылын; сідзкӧ ∆CDM-ӧс позьӧ вежны сыкӧд ӧтгырся DKM куимпельӧсаӧн. Та ногӧн сетӧм куимпельӧсаса площадь джын ыджда ACM куимпельӧсалысь площадь позьӧ вежны ADK куимпельӧсаса ӧтыджда площадьӧн.

Тадз, DK веськыд сетӧм ABC куимпельӧсаӧс торйӧдӧ кык ӧтгырся юкӧнӧ: ∆ADK да BCDK нёльпельӧсаӧ.

Юасянъяс да упражненньӧяс.

1. Кыдз вежсяс веськыднёльпельӧсалӧн площадь, сылысь кӧ подувтас a кольны вежтӧг, а судта h 1) ыдждӧдны 3-ысь, 2) ичӧтмӧдны 2-ысь?

2. Кымын пӧв ыдждас квадратлӧн площадь, кор сылысь быд бок ыдждӧдан куим пӧв?

3. Вермасны-ӧ лоны ӧтгырсяӧн разнӧй подувтасъяса да разнӧй судтаяса веськыднёльпельӧсаяс?

4. Кузь-ӧ колӧ лоны 160 м пасьта веськыднёльпельӧса му участок, сійӧн кӧ вежны 200 м кузя квадратнӧй формаа му участокӧс?

5. Веськыднёльпельӧсалӧн да квадратлӧн ӧткузяӧсь периметръяс. Веськыднёльпельӧсалӧн ӧти бок 90 см кузя, квадратлӧн бок = 60 см. Кодыслӧн налӧн ыджыдджык площадь да унаӧн-ӧ?

6. Веськыднёльпельӧса да квадрат ӧтгырсяӧсь. Веськыднёльпельӧсаын ӧти бок = 120 см; квадратлӧн бок = 60 см. Кодыслӧн налӧн ичӧтджык периметр да унаӧн-ӧ?

7. Докажитны, мый параллелограммын диагональясӧн артман 4 куимпельӧса ӧтгырсяӧсь.

8. Параллелограммын ичӧтджык диагональ n = 5 см перпендикулярнӧй кутшӧмкӧ ӧти боклы да сыкӧд ӧтыджда. Артавны параллелограммлысь площадь.

9. Докажитны, мый нёльпельӧсалӧн площадь, кодлӧн йывъяс куйлӧны сетӧм параллелограммса бокъяс шӧрын, параллелограмм площадь джын ыджда.

10. Кык ӧткузя бока трапецияын диагональяс вомӧнасьӧны веськыд пельӧс улын. Трапециялӧн судта = h. Докажитны, мый трапециялӧн площадь S = h².

11. Трапецияӧс пӧртны сыкӧд ӧтгырся 1) параллелограммӧ, 2) веськыднёльпельӧсаӧ.

12. a = 5 см подувтаса да h = 8 см судтаа ёсьпельӧса куимпельӧсаӧс пӧртны сыкӧд ӧтгырся веськыднёльпельӧсаӧ, кодлӧн подувтас мед вӧлі сійӧ жӧ, кутшӧм и куимпельӧсалӧн.

13. Сетӧма ABCD трапеция. Докажитны, мый параллельнӧй бокъяслысь K да L шӧръяс ӧтлаалан веськыд визь трапецияӧс торйӧдӧ кык ӧтгырся трапецияӧ.

14. Вӧчны квадрат, кодлӧн площадь мед вӧлі сетӧм квадрат площадьысь ыджыдджык кык пӧв.

Индӧд. Используйтны сетӧм квадратлысь диагональ.

X. ГЕОМЕТРИЧЕСКӦЙ МЕСТАЯС.

1 §. Визь кыдз чутъяслӧн геометрическӧй места

Кытшвизь вывса чутъяслӧн эм татшӧм свойство: найӧ ставныс куйлӧны ӧти чутсянь, кытшвизь шӧрчутсянь, ӧти сійӧ жӧ ылнакост сайын, коді кытшвизь радиус ыджда.

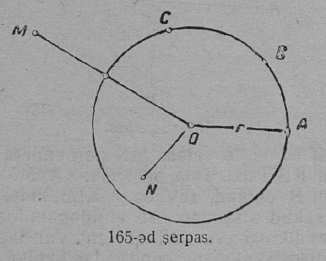
Тайӧ свойствосӧ плоскосьт вылын кутӧны сӧмын сэтшӧм чутъяс, кодъяс куйлӧны сетӧм кытшвизь вылын; сэтшӧм чутъяс, кодъяс куйлӧны сійӧ жӧ плоскосьт вылын, кыдзи и кытшвизьыс, но оз куйлыны тайӧ кытшвизьыс вылын, тайӧ свойствосӧ оз кутны.

Сетӧма кӧ O чутын шӧрчута кытшвизь, кодлӧн радиус r = 3 см, любӧй A, B да C чутъясыс, кодъяс шӧрчутсянь 3 см сайын, куйлӧны сетӧм кытшвизь вылын.

Быд M чут, коді O шӧрчутсянь 3 см-ысь ылынджык, кор OM > r, куйлӧ сетӧм кытшвизь сайын; кор N чутсянь O шӧрчутӧдз ылнакостыс радиусысь ичӧтджык, кор NO < r, N чут куйлӧ кытшвизь пытшкын. Сідзкӧ, 1) сетӧм кытшвизь вылын куйлысь чутъяс кутӧны определённӧй свойствояс: найӧ ставныс ӧтылнаын ӧти чутсянь, шӧрчутсянь; 2) чутъяс, кодъяс оз куйлыны сетӧм кытшвизь вылын, татшӧм свойствосӧ оз кутны.

Визьяс, кыдз, пример вылӧ, кытшвизь, кодъяслӧн став чутъясыс кутӧны кутшӧмкӧ определённӧй свойство (на вылын не куйлысь чутъяс оз кутны тайӧ свойствосӧ), шусьӧны сетӧм свойствоӧн обладайтысь чутъясса геометрическӧй местаӧн.

2 §. Геометрическӧй местаяс.

1. Кытшвизь эм ӧти чутсянь — кытшвизь шӧрчутсянь сетӧм ылнаӧдз ылысмӧдӧм чутъяслӧн плоскосьт вылын геометрическӧй места.

2. Теорема. Вундӧг шӧр пыр нуӧдӧм сылы перпендикуляр эм вундӧг помъяссянь ӧтылнаӧ ылысмӧдӧм чутъяслӧн геометрическӧй места.

Сетӧма: AC = CB; MN ⊥ AB; D, E, F... MN перпендикуляр вылын чутъяс (166 серп.).

______________________________________________

Колӧ докажитны: DA = DB; EA = EB; FA = FB...

Докажитӧм. D, E, F да с. в. чутъяс ӧтлаалам вундӧг A да B помъяскӧд. Лоӧны вундӧгъяс DA да DB, EA да EB, FA да FB да с. в. Тайӧ вундӧгъяс гозйӧн-гозйӧн ӧтыдждаӧсь кыдз ӧти чутысь петысь пӧлыняяс да кодъяслӧн AC да CB проекцияяс ӧтыдждаӧсь; сідзкӧ, DA = DB, EA = EB, FA = FB да с. в. Та ногӧн AB вундӧг шӧр пыр мунысь перпендикулярлӧн любӧй чут вундӧгса A да B помъяссянь ӧтылнаын.

Босьтам произвольнӧй K чут, коді оз куйлы сетӧм MN перпендикуляр вылын (167 серп.), сэк KA абу KB ыджда. Тайӧ петӧ тадз: KA MN-кӧд вомӧнасянін L чут ӧтлаалам B чуткӧд, сэк лоӧ ∆KLB, кытысь: KB < KL + LB. LB вундӧг вежам сыкӧд ӧтыдждаӧн: AL вундӧгӧн; лоӧ KB < KL + LA. Сідзкӧ, MN перпендикуляр вывса любӧй чут вундӧг помъяссянь ӧтылнаын; любӧй чут, коді оз куйлы перпендикуляр вылын, тайӧ свойствосӧ оз кут. Тадз, AB вундӧг C шӧрті нуӧдӧм MN перпендикуляр эм вундӧг помъяссянь ӧтылнаӧ ылысмӧдӧм чутъяслӧн геометрическӧй места.

3. Теорема. Пельӧслӧн биссектриса эм пельӧс бокъяссянь ӧтылнаӧ ылысмӧдӧм чутъяслӧн геометрическӧй места.

Сетӧма: BD — биссектриса; ∠1 = ∠2 (168 серп.).

ME ⊥ AB да MF ⊥ BC; NK ⊥ AB да NL ⊥ BC да с. в.

___________________________

Колӧ докажитны: ME = MF; NK = NL да с. в.

Докажитӧм. ∆MBE = ∆MBF: налӧн BM — ӧтувъя гипотенуза, ∠1 = ∠2. Сідзкӧ: ME = MF. Дзик жӧ тадз докажитӧны, мый NK = NL.

Босьтам произвольнӧй P чут, коді оз куйлы BO биссектриса вылын (169-ӧд серп.), B пельӧс бокъяссянь PP₁ да PP₂ ылнакостъясыс абу ӧтыдждаӧсь. Докажитам тайӧс. PP₂ да BD вомӧнасянін O чутсянь BC боклы нуӧдам OQ перпендикуляр, OQ = OP₂; но PP₁ перпендикуляр PQ пӧлыняысь ичӧтджык, PP₁ < PQ; мӧдарсянь, ∆OPQ куимпельӧсаысь петӧ: PQ < PO + OQ; сідзкӧ дерт нин PP₁ < PO + OQ. Бӧръя неравенствоын OQ вежам сыкӧд ӧтыджда OP₂ вундӧгӧн, лоӧ: PP₁ < PO + OP₂, либӧ PP₁ < PP₂.

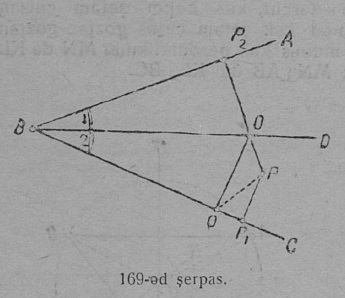
Сідз, BD биссектриса вылын куйлысь любӧй чут B пельӧс бокъяссянь ӧтылнаын; любӧй чут, коді оз куйлы BD биссектриса вылын, тайӧ свойствоӧн оз обладайт. Тадз, пельӧслӧн биссектриса эм пельӧс бокъяссянь ӧтылнаӧ ылысмӧдӧм чутъяслӧн геометрическӧй места.

4. Сетӧм веськыдсянь ӧтылнаӧ ылысмӧдӧм чутъяслӧн геометрическӧй местаӧн лоӧны кык веськыд визь, кодъяс сетӧм веськыдкӧд параллельнӧйӧсь да сысянь мунӧны ӧтарас и мӧдарас ӧти сійӧ жӧ расстоянньӧ сайын.

5. Ӧти сійӧ жӧ подувтаса да ӧтыджда судтаяса куимпельӧсаяслӧн йывъяслӧн геометрическӧй местаӧн лоӧны кык веськыд, подувтаскӧд параллельнӧйӧсь, кодъяс мунӧны сысянь ӧтарас и мӧдарас куимпельӧсаяс судта ылнаын.

Юасянъяс.

1. Мый лоӧ геометрическӧй местаӧн чутъяслӧн, кодъяс кык вомӧнасян веськыд визьысь ӧтылнаын?

2. Мый лоӧ геометрическӧй местаӧн чутъяслӧн, кодъяс кык веськыд параллельнӧйясысь ӧтылнаын?

XI. КЫТШВИЗЬ ДА КРУГ.

1 §. Кытшвизь.

Кытшвизь тырбура определитчӧ, кор сылысь сетӧма шӧрчут да радиус; радиус кытшвизьлысь определяйтӧ размер, а шӧрчут — положенньӧ.

1. Ӧти A чут пыр, коді абу шӧрчут, плоскосьт вылын позьӧ нуӧдны помтӧм уна кытшвизь (170 серп.); быд кытшвизьлысь шӧрчутсӧ плоскосьт вылын позьӧ босьтны кӧн колӧ.

2. Ӧти плоскосьт вылын A да B кык чут пыр сідзжӧ позьӧ нуӧдны помтӧм уна кытшвизь (171 серп.), кодъяслӧн шӧрчутъяс оз лоны кӧн колӧ плоскосьт вылын, кыдз вӧлі 1-я случайын, а найӧ лоӧны A да B помъяса AB вундӧг O шӧр пыр мунысь перпендикуляр вылын.

Збыльысь ӧд, условийӧ кузя A да B чутъяслы (AB вундӧг помъяслы) колӧ куйлыны кытшвизь вылын; сідзкӧ, кытшвизьлӧн шӧрчутыс насянь ӧтылнаын; а вундӧг помъяссянь ӧтылнаӧ ылысмӧдӧм чутъяслӧн геометрическӧй места эм вундӧг шӧр пыр мунысь перпендикуляр.

3. A, B да C куим чут пыр, кодъяс оз куйлыны ӧти веськыд визь вылын (172 серп.), позьӧ нуӧдны кытшвизь дай сӧмын ӧтиӧс. Сылӧн шӧрчут, кыдз куим сетӧм чутсянь ӧтылнаӧ ылысмӧдӧм чут, куйлӧ быд кык сетӧм чутӧс гозйӧн-гозйӧн ӧтлаалысь вундӧгъясса шӧръяс пыр мунысь перпендикуляр MN да KL мӧда-мӧдкӧд вомӧнасянінын: MN ⊥ AB да KL ⊥ BC.

Перпендикуляръяс MN да KL вомӧнасьӧны кыдз AB да BC кык вомӧнасян веськыд визьяс дорӧ перпендикуляръяс. O чутыс, тайӧ перпендикуляръясыс вомӧнасянін чутыс лоӧ кытшвизьлӧн шӧрыс, тадзсӧ сы вӧсна, мый сійӧ ӧтылнаын A, B да C чутъяссянь: AO = OB = OC = кытшвизьса r-лы. Кык веськыд визь MN да KL вомӧнасьӧны сӧмын ӧти чутын. Сідзкӧ A, B да C куим чут пыр позьӧ нуӧдны сӧмын ӧти кытшвизь.

Куим чут, кодъяс оз куйлыны ӧти веськыд визь вылын, тырвыйӧ определяйтӧны кытшвизьлысь положенньӧ да размер.

4. Куим чут кӧ A, B да C куйлӧны ӧти веськыд визь вылын, AB да BC шӧръяс пыр нуӧдӧм MN да KL перпендикуляръяс, кыдз ӧти сійӧ жӧ веськыд визь вылӧ нуӧдӧм перпендикуляръяс, лоӧны параллельнӧйӧсь: налӧн ӧтувъя чут абу. Таысь петӧ, мый ӧти веськыд вылын куйлысь куим чут пыр — A, B да C — кытшвизьӧс нуӧдны он вермы. Сідзкӧ, веськыд визьлӧн оз вермы лоны кытшвизькӧд куим ӧтувъя чут.

Веськыд визь вомӧналӧ кытшвизьӧс сӧмын кык чутын.

2 §. Хордалы перпендикулярнӧй диаметрлӧн свойство. Кругын симметрия.

1. Теорема. Хордалы перпендикулярнӧй диаметр шӧри юкӧ хордасӧ да сыӧн стягивайтан дугасӧ.

Сетӧма: DD₁ — диаметр; AB — хорда; DD₁ ⊥ AB (173 серп.).

_______________________________

Колӧ докажитны: 1) AC = CB; 2) ‿AD = ‿BD; 3) ‿AD₁ = ‿BD₁.

Докажитӧм. AB хордалӧн помъясыс — A да B чутъяс, кыдз кытшвизь вылын куйлысьяс, ӧтылнаынӧсь O шӧрчутсянь, коді куйлӧ AB хордалы перпендикулярнӧй DD₁ диаметр вылын. AOB куимпельӧсаыс — кык ӧткузя бока да AB-лы OC перпендикулярыс — сылӧн симметрия ось. Татысь петӧ, мый CA = CB, либӧ хордалы перпендикулярнӧй диаметр сійӧс юкӧ шӧри. Кусыньтны кӧ кругсӧ DD₁ диаметр кузя, кытшвизь юксяс шӧри сы вӧсна, мый DAD₁ дугалӧн чутъяс ӧтлаасясны DBD₁ дугаса чутъяскӧд; тайӧ лоӧ: диаметрыс лоӧ круглӧн да кытшвизьлӧн симметрия ось. Таысь ӧтдор, ‿AD вевсяасяс ‿BD-кӧд да ‿AD₁ вевсяасяс ‿BD₁-кӧд, либӧ мӧд ног кӧ, хордаӧн стягивайтан дугаяс хордаыслы перпендикулярнӧй диаметрӧн юксьӧны шӧри.

2. Кругын позьӧ нуӧдны помтӧм уна диаметр; сідзкӧ, кругын помтӧм уна симметрия ось.

Осевӧй симметрияысь ӧтдор, кругын либӧ кытшвизьын нӧшта эм центральнӧй симметрия: тайӧ лоӧ, мый кругын да кытшвизь вылын эм помтӧм уна чут гоз, кодъяс шӧрчут серти куйлӧны симметричнӧя. Татшӧм чутъяс куйлӧны шӧрчут пыр мунысь веськыд вылын да шӧрчутсянь ӧтылнаынӧсь.

Любӧй диаметрлӧн помъяс — чутъяс A да A₁, D да D₁ (174 серп.) — O шӧрчут серти симметричнӧйӧсь; кытшвизь пытшкын куйлысь B да B₁ чутъяс O шӧрчут серти симметричнӧйӧсь; найӧ куйлӧны шӧрчут пыр мунысь веськыд вылын да шӧрчутсянь ӧтылнаынӧсь: OB = OB₁.

3. Задача. Сетӧм AB дугаӧс юкны шӧри (175 серп.).

Построенньӧ. Шӧрчутсянь AB хордалы нуӧдам перпендикуляр да нюжӧдам сійӧс AB дугакӧд D чутын вомӧнасьтӧдз, сэк ‿AD = ‿BD. Шӧрчутлысь кӧ местасӧ абу индӧма, сэк AB хорда шӧр пыр нуӧдам OP перпендикуляр, коді AB дугаӧс D чутын юкас шӧри.

3 §. Параллельнӧй хордаяс костӧ йӧртӧм дугаяс свойство.

Теорема. Параллельнӧй хордаяс костӧ йӧртӧм дугаяс ӧтыдждаӧсь.

Сетӧма: AB да CE — хордаяс; AB ∥ CE (176 серп.).

____________________________

Колӧ докажитны: ‿AC = ‿BE.

Докажитӧм. Нуӧдам D₁D диаметр AB да CE хордаяслы перпендикулярнӧя. D₁D диаметр кузя кӧ кусыньтам кругсӧ, вевсяасясны: A чут B чуткӧд, C чут E чуткӧд да AC дуга BE дугакӧд; сідзкӧ, ‿AC = ‿BE.

4 §. Кытшвизьлысь да дугалысь шӧрчутсӧ корсьӧм.

1. Задача. Сетӧма кытшвизь, кодлысь шӧрчутсӧ абу индӧма. Корсьны шӧрчутсӧ.

Построенньӧ. Сетӧм кытшвизь вылын босьтам куим любӧй чут — A, B, C, нуӧдам хордаяс — AB да BC (177 серп.) да найӧ E да F шӧръяс пыр нуӧдам налы KL да MN перпендикуляръяс.

Кыкнан перпендикулярыс мунасны кытшвизь шӧрчут пыр; корсян шӧрчут кутас куйлыны MN перпендикуляр вылын да KL перпендикуляр вылын, буретш найӧ вомӧнасянін O чутын. O чутӧс A, B да C чутъяскӧд ӧтлаалӧм бӧрын лоӧ: AO = OB = OC; сідзкӧ, A, B да C чутъяс O чутсянь ӧтылнаынӧсь, а сы вӧсна, мый найӧ условийӧ серти куйлӧны кытшвизь вылын, O чут лоӧ кытшвизьлы шӧрчутӧн.

2. Задача. Сетӧма дуга. Корсьны шӧрчут.

Построенньӧ. Дугалысь шӧрчутсӧ корсьӧм вылӧ вӧчам сэтшӧм жӧ построенньӧ, кутшӧмӧс вӧчим кытшвизьлысь шӧрчутсӧ корсьӧм вылӧ.

5 §. Хордаяс да дугаяс костын зависимосьт.

Теорема. Ӧти кругын (либӧ ӧтыджда кругъясын) ӧтыджда хордаяс стягивайтӧны ӧтыджда дугаясӧс да, мӧдарӧ, ӧтыджда дугаяс стягивайтӧны ӧтыджда хордаясӧс.

1. Сетӧма: AB = CD (178 серп.).

__________________________

Колӧ докажитны: ‿AB = ‿CD.

2. Сетӧма: ‿AB = ‿CD.

__________________________

Колӧ докажитны: AB = CD.

Докажитӧм. 1. AB да CD хордаяслысь помъяссӧ ӧтлаалам O шӧрчуткӧд, лоӧны кык ӧтыджда куимпельӧса: AOB да COD; налӧн AB = CD условийӧ серти, AO = OC да BO = OD, кыдз ӧти сійӧ жӧ кытшвизьлӧн радиусъяс.

Куимпельӧсаяс равенствоысь петӧ, мый ∠AOB = ∠COD; ӧтыджда центральнӧй пельӧсъяслы соответствуйтӧны ӧтыджда дугаяс, та вӧсна ‿AB = ‿CD.

2. ‿AB = ‿CD, та вӧсна ӧтыдждаӧсь налы соответствуйтысь центральнӧй пельӧсъяс: ∠AOB = ∠COD. AOB да COD куимпельӧсаясын AO да OC, BO да OD бокъяс ӧтыдждаӧсь, кыдз ӧти сійӧ жӧ кытшвизьлӧн радиусъяс; сідзжӧ ӧтыдждаӧсь на костса пельӧсъяс; сідзкӧ ∆AOB = ∆COD; татысь петӧ, мый AB да CD хордаяс ӧтыдждаӧсь: AB = CD.

6 §. Хордаяс кост зависимосьт да шӧрчутсянь наӧдз расстоянньӧяс кост зависимосьт.

1. Теорема. Ӧти кругын (либӧ ӧтыджда кругъясын) ӧтыджда хордаяс шӧрчутсянь ӧтылнаынӧсь да, мӧдарӧ, шӧрчутсянь ӧтылнаӧ ылысмӧдӧм хордаяс ӧтыдждаӧсь.

1) Сетӧма: AB = CD; OE ⊥ AB да OF ⊥ CD (178 серп.).

_________________________________

Колӧ докажитны: OE = OF.

Докажитӧм. AOB да COD куимпельӧсаяс равенствоысь петӧ, мый налӧн судтаяс ӧтыдждаӧсь: OE = OF.

2) Сетӧма: OE ⊥ AB да OF ⊥ CD, OE = OF.

____________________________________

Колӧ докажитны: AB = CD.

Докажитӧм. AOE да COF веськыдпельӧса куимпельӧсаясын AO = CO, кыдз радиусъяс, да OE = OF условийӧ серти; та вӧсна ∆AOE = ∆COF; татысь петӧ, мый AE = CF; AE лоӧ AB хордалӧн, а CF — CD хордалӧн джынъяс; джынъяс кӧ ӧтыдждаӧсь, ӧтыдждаӧсь быдсаяс; сідзкӧ AB = CD.

2. Теорема. Кытшвизьын кык хордаысь ичӧтджыкыс сійӧ, коді шӧрчутсянь ылынджык да, мӧдарӧ, ыджыдджык хорда — шӧрчутсянь матынджык.

Сетӧма: O кытшвизь да AB хорда > DE хордаысь (179 серп.).

________________________________________

Колӧ докажитны: OK < OL.

Докажитӧм. AB хорда A помсянь нуӧдам AC хорда = DE; сэк найӧ лоӧны шӧрчутсяньыс ӧтылнаынӧсь: OM = OL. Ӧтлаалам KM веськыдӧн K да M да видлалам KAM куимпельӧсаӧс. Сыын AK > AM, кыдз абу ӧтыджда AB да AC хордаяслӧн джынъяс; та вӧсна ∠2 > ∠1 (куимпельӧсаын ыджыдджык бок водзын куйлӧ ыджыдджык пельӧс). KOM куимпельӧсаын: ∠3 = 90° − ∠2 да ∠4 = 90° − ∠1. Тайӧ равенствояслысь веськыдвыв пайяс (90° − ∠2 да 90° − ∠1 разносьтъяс) ӧтластитӧмысь аддзам, мый ∠2 чинтан ∠1 чинтанысь ыджыдджык; сідзкӧ 90° − ∠2 < 90° − ∠1; та вӧсна ∠3 < ∠4; куимпельӧсаын ичӧтджык пельӧс водзын куйлӧ ичӧтджык бок; сідзкӧ, OK < OM. OM-ӧс сыкӧд ӧтыджда OL вундӧгӧн вежӧм бӧрын лоӧ: OK < OL, мый колӧ вӧлі докажитны.

7 §. Веськыд визьлӧн кытшвизь серти различнӧй положенньӧяс. Вундысь да касательнӧй.

1. Веськыд визьлӧн ас положенньӧыс серти кытшвизькӧд вермас лоны: 1) кык ӧтувъя чут, 2) сӧмын ӧти ӧтувъя чут, 3) ньӧти ӧтувъя чут.

Веськыд визьлӧн кытшвизькӧд кыкысь уна ӧтувъя чут оз вермы лоны сы вӧсна, мый ӧти веськыд визь вылын куйлысь куим чут пыр кытшвизьӧс нуӧдны оз позь.

2. MN веськыдлӧн (180 серп.), коді вомӧналӧ кытшвизьӧс, кытшвизьыскӧд эм кык ӧтувъя чут: A да B; татшӧм веськыд шусьӧ вундысьӧн; MN вундысьлӧн AB вундӧг, кодлӧн A да B помъясыс куйлӧны кытшвизь вылын, лоӧ AB хорда. MN вундысь шӧрчутсяньыс OP ылнаын, та дырйи OP ⊥ MN да OP < r.

Шӧрчут пыр мунысь вундысь шусьӧ центральнӧй вундысьӧн да лоӧ кытшвизьлӧн симметрия ось.

3. MN вундысьӧс кӧ кутам аслыс параллельнӧя шӧрчутсянь ылысмӧдны: 1) сылӧн пытшкӧс пай, AB хорда, кутас водзысь-водзӧ ичӧтмыны, AB > A₁B₁ > A₂B₂...; 2) шӧрчутсянь сыӧдз ылнакостыс кутас содны, OP < OP₁ < OP₂...; 3) кытшвизькӧд вомӧнасянін A да B чутъяс мӧда-мӧд дінӧ матысмӧны.

MN веськыд ас мунігас вермас воны сэтчӧдз, мый сылӧн кытшвизькӧд вомӧнасянін дорса кыкнан чутыс — A да B — ӧтлаасясны ӧти K чутӧ да вундысьлӧн пытшкӧс пайыс — AB хорда — пӧрӧ чутӧ.

MN вундысь татшӧм положенньӧ дырйи (181 серп.) шусьӧ касательнӧйӧн; сылӧн кытшвизькӧд ӧтувъя K чут шусьӧ инман чутӧн (касанньӧ чутӧн). Касательнӧйлӧн шӧрчутсянь OK ыджда расстоянньӧ лоӧ кытшвизь радиус: OK = r. Тадз, веськыд визь, кодлӧн кытшвизькӧд сӧмын ӧти ӧтувъя чут, шусьӧ касательнӧйӧн; шӧрчутсянь сыӧдз лоӧ радиус ыджда расстоянньӧ.

4. MN веськыдлӧн (182 серп.), кытчӧдз шӧрчутсянь радиусысь ылынджык, OL > r, кытшвизькӧд ӧтувъя чутъяс абуӧсь; сэтшӧм веськыдыд — кытшвизь сайын.

Тадз, MN веськыдлӧн шӧрчут серти положенньӧ определяйтчӧ шӧрчутсянь сыӧдз d расстоянньӧӧн: d < r, MN — вундысь; 2) d = r, MN — касательнӧй; 3) d > r, MN — кытшвизь сайын.

5. Теорема. Касательнӧй — касанньӧ чутӧ нуӧдӧм радиуслы перпендикуляр.

Сетӧма: MN — касательнӧй; K — касанньӧ чут (181 серп.).

_________________________________

Колӧ докажитны: OK ⊥ MN.

Докажитӧм. MN касательнӧй вылын кӧнкӧ босьтам L чут да ӧтлаалам сійӧс O шӧрчуткӧд. L чут куйлӧ кытшвизь сайын, та вӧсна сыӧдз расстоянньӧ лоӧ радиусысь кузьджык: OL > OK. Та ногӧн OK лоӧ O чутсянь касанньӧ чутӧдз меддженьыд расстоянньӧ; а чутсянь веськыдӧдз меддженьыд расстоянньӧ лоӧ перпендикуляр; тадз, OK ⊥ MN.

6. Теорема (мӧдара). Кытшвизь вылын куйлысь радиуслы помас перпендикулярнӧй быд веськыд визь лоӧ касательнӧй.

Сетӧма: MN ⊥ OK (181 серп.).

_________________________

Колӧ докажитны: MN — касательнӧй.

Докажитӧм. OK перпендикуляр дженьыдджык MN веськыд визь вылӧ O чутсянь нуӧдӧм быд мӧд OL веськыдысь, та вӧсна OL > OK да L чут куйлӧ кытшвизь сайын. K чут — MN веськыд визь вылын сӧмын ӧти сэтшӧм чут, коді ӧттшӧтш куйлӧ кытшвизь вылын; MN веськыд, кодлӧн кытшвизькӧд сӧмын ӧти ӧтувъя K чут, — касательнӧй.

8 §. Касательнӧйясӧс нуӧдӧм.

1. Задача. Кытшвизь вылын сетӧм K чут пыр нуӧдны кытшвизь бердӧ касательнӧйӧс (181 серп.).

Решитӧм. Сетӧм K чутӧ нуӧдам OK радиус да веськыд визь MN ⊥ OK. OK-лы тайӧ MN перпендикуляр лоӧ корсян касательнӧйӧн.

2. Задача. Сетӧм кытшвизьлы нуӧдны касательнӧйӧс сідз, медым сійӧ вӧлі сетӧм AB веськыдлы параллельнӧй (183 серп.).

Решитӧм. O шӧрчут пыр нуӧдам веськыд визь CD ⊥ AB; тайӧ веськыд визьыс вундас кытшвизьӧс кык чутын — K да K₁. Тайӧ K да K₁ чутъяс пыр нуӧдам KK₁ диаметрлы перпендикулярнӧй MN да M₁N₁ веськыдъясӧс. Тайӧ кыкнан веськыдыс лоӧны корсян касательнӧйясӧн.

3. Задача. Сетӧм кытшвизьлы нуӧдны касательнӧйӧс ортсыс A чутсянь (184 серп.).

1) Шуам, задачасӧ решитӧма да сетӧм O шӧрчута кытшвизьын A чутсянь нуӧдӧма индӧм кытшвизьлы AK₁ касательнӧйӧс. O чутӧс K₁ чуткӧд ӧтлаалӧм бӧрын лоӧ веськыдпельӧса AOK₁ куимпельӧса. OK₁ радиусӧс нюжӧдӧм вылӧ пуктам вундӧг K₁B₁ = OK₁ = r. B₁ чутӧс A чуткӧд ӧтлаалӧм бӧрын лоӧ кык ӧткузя бока AOB₁ куимпельӧса, кӧн AK₁ лоӧ судтаӧн сы вӧсна, мый сійӧ — медиана. Та ногӧн, задача пӧрӧ кык ӧткузя бока AOB₁ куимпельӧсалысь коймӧд B₁ йыв корсьӧмӧ, кодлысь сетӧма нин кык йывсӧ: A чут да O — сетӧм кытшвизьлӧн шӧрыс; AO лоӧ куимпельӧсалӧн боквывса бокыс. B₁ чут куйлӧ: 1) A чутын шӧрчута да A чутсянь O шӧрчутӧдз расстоянньӧ ыджда AO радиуса кытшвизь вылын да 2) O чутын шӧрчута да сетӧм кытшвизь диаметр ыджда радиуса кытшвизь вылын; та вӧсна B₁ чут эм кыкнан кытшвизьлӧн вомӧнасянін чут.

2) Построенньӧ. Нуӧдам сетӧм кытшвизь диаметр ыджда радиусӧн O чутын шӧрчута первойя отсасьысь кытшвизь, сэсся A чутсӧ шӧрчут пыдди босьтӧмӧн нуӧдам мӧд отсасьысь кытшвизь, кодлӧн радиусыс лоӧ OA ыджда — A чутсянь сетӧм кытшвизьса O шӧрчутӧдз расстоянньӧ ыджда. Отсасьысь кытшвизьяслысь вомӧнасянін B₁ да B₂ чутъяссӧ ӧтлаалам O шӧрчуткӧд. OB₁ да OB₂ сетӧм кытшвизьӧс вундӧны K₁ да K₂ чутъясын, кодъяс лоӧны касанньӧ чутъясӧн AK₁ да AK₂ кык касательнӧйяслӧн, кодъясӧс нуӧдӧма сетӧм кытшвизь вылӧ A чутсянь.

3) Докажитӧм. B₁ чутӧс A чуткӧд ӧтлаалӧм бӧрын лоӧ кык ӧткузя бока AB₁O куимпельӧса, кӧн AO = AB₁ — кыдз A чутын шӧрчута кытшвизьлӧн радиусъяс; таысь ӧтдор, сы вӧсна, мый OB₁ = 2OK₁ — построенньӧ серти, K₁ чут эм OB₁-лӧн шӧр; татысь петӧ, мый кык ӧткузя бока AOB₁ куимпельӧсаын AK₁ веськыд лоӧ медиана дай судта, сідзкӧ сійӧ K₁ чутын OB₁-лы перпендикулярнӧй. Тадз, AK₁ ⊥ OK₁, мӧд ног кӧ шуны, AK₁ веськыд визьыс перпендикулярнӧй OK₁ радиуслы сійӧ K₁ помын, коді куйлӧ кытшвизь вылас; сідзкӧ сійӧ сетӧм кытшвизьлы лоӧ K₁ чутын касательнӧйӧн. Тадз жӧ артмӧ, мый AK₂ веськыд визьыс — мӧд касательнӧй, кодӧс нуӧдӧма A ортсыс чутсяньыс сетӧм кытшвизьлы.

4) Кык кытшвизь вомӧнасьӧны кык чутын — K₁ да K₂ чутъясын; сідзкӧ, тайӧ задачасӧ позьӧ кык ног решитны: кытшвизь сайын куйлысь A чутсянь сетӧм кытшвизьлы позьӧ нуӧдны кык касательнӧйӧс — AK₁ да AK₂.

Касательнӧй кузьта пыдди босьтӧны вундӧг, кодлӧн помъясыс — сетӧм A чут да касанньӧ чутъяс — K₁ либӧ K₂.

9 §. Ӧти сійӧ жӧ чутысь нуӧдӧм касательнӧйяслӧн свойство.

1. Теорема. Кытшвизь сайын куйлысь чутсянь кытшвизьлы нуӧдӧм касательнӧйяс ӧтыдждаӧсь.

Сетӧма: AK₁ да AK₂ — касательнӧйяс, K₁ да K₂ — касанньӧ чутъяс (184 серп.).

_________________________

Колӧ докажитны: AK₁ = AK₂.

Докажитӧм. Веськыдпельӧса AOK₁ да AOK₂ куимпельӧсаяс равнӧйӧсь; налӧн OA бок — ӧтувъя гипотенуза, а OK₁ = OK₂ кыдз радиусъяс. Куимпельӧсаяс равенствоысь петӧ, мый AK₁ = AK₂.

2. Сійӧ жӧ куимпельӧсаяс равенствоысь петӧ, мый ∠OAK₁ = ∠OAK₂, кытысь лоӧ, мый OA лоӧ ӧти чутысь петан кык касательнӧйӧн артмӧм A пельӧслӧн биссектриса.

AO центральнӧй вундысь лоӧ A пельӧс симметриялӧн ось, — тайӧ пельӧссӧ артмӧдӧны касательнӧйяс, кодъясӧс нуӧдӧма ортсыса A чутсянь сетӧм кытшвизьлы.

3. Шӧрчуткорсьысь. Кытшвизьлысь шӧрчутсӧ корсьӧм вылӧ эм прибор, кодӧс шуӧны шӧрчуткорсьысьӧн. Сылысь устройствосӧ петкӧдлӧма 185 серпас вылын. Сійӧс вӧчӧма веськыд пельӧс улын крепитӧм AB да AC планкаясысь да коймӧд AD планкаысь, кодлӧн ӧти дорышыс мунӧ веськыд пельӧс биссектриса кузя. Тайӧ приборлысь уджсӧ подулалӧма сы вылӧ, мый кык касательнӧйӧн артмӧм пельӧслӧн биссектриса мунӧ круг шӧрчут пыр.

Шӧрчуткорсьысьӧс колӧ кыкысь пуктыны круг бердӧ, кодлысь корсьӧны шӧрчутсӧ, да AD планка T дорыш бердтіыс быд пӧв нуӧдны веськыдъясӧс; налӧн вомӧнасянін лоӧ O шӧрчут.

Шӧрчуткорсьысь йывсянь касанньӧ чутӧдз ылнакостыс круг радиус ыджда сы вӧсна, мый шӧрчуткорсьысь доръяслӧн кытшвизькӧд касанньӧ чутъясӧ нуӧдӧм радиусъясыс доръясыскӧд вӧчӧны квадрат.

Юасянъяс да упражненньӧяс.

1. Кыдз корсьны кытшвизьвывса A чутлы центральнӧ-симметричнӧй чут?

2. Мыйӧн торъялӧны касательнӧй да вундысь?

3. Мый ыджда кык параллельнӧй касательнӧй костса расстоянньӧыс?

4. Докажитны, мый хордалы параллельнӧй касательнӧй хордаӧн стягивайтан дугаӧс юкӧ шӧри касанньӧ чутас.

5. Мый лоӧ сетӧм A чут пыр мунысь 3 см ыджда радиусъяса кытшвизьяс шӧрчутъяслӧн геометрическӧй местаӧн? Вӧчны чертёж.

6. 4 см ыджда радиуса кытшвизьын нуӧдны 4 см кузя хорда сідз, медым сійӧ муніс кытшвизь вылын сетӧм A чут пыр. Кымын татшӧм хорда позьӧ нуӧдны?

7. O шӧрчута круг пытшкын сетӧм A чут пыр нуӧдны MN хорда сідз, медым сійӧ A чутын юксис шӧри.

8. Кытшвизьвывса A чут пыр нуӧдӧма мӧда-мӧдлы перпендикулярнӧй да мӧда-мӧдкӧд ӧтыджда кык хорда; шӧрчутсянь наӧдз 3 см. Артавны хордаяслысь кузьтанысӧ.

9. Нуӧдны кытшвизьӧс сідз, медым сійӧ касайтчис MN веськыд визь бердӧ P чутас. Исследуйтны, кымын кытшвизь позьӧ нуӧдны, да индыны, кӧн кутасны налӧн шӧрчутъясыс куйлыны.

10. Сетӧма a = 5 см бока ABCD квадрат. Нуӧдны кык кытшвизь сідз, медым квадратлӧн бокъясыс ӧттшӧтш вӧліны ӧти кытшвизьлы хордаясӧн, а мӧдлы касательнӧйясӧн.

11. Нуӧдны 3 см да 5 см ыджда радиусъяса кык концентрическӧй кытшвизь. Сэсся ыджыд кытшвизьын нуӧдны кык параллельнӧй хорда сідз, мед найӧ ичӧт кытшвизьлы вӧліны касательнӧйясӧн. Докажитны, мый тайӧ хордаяс ӧтыдждаӧсь.

12. A чут куйлӧ кытшвизь сайын. 1) Построенньӧӧн корсьны сысянь кытшвизьӧдз медматыс да медылыс расстоянньӧ.

Индӧд. Чутсянь кытшвизьӧдз медматыс^да медылыс? — А. В./^ расстоянньӧӧн шуӧны центральнӧй вундысьлысь вундӧг, кодлӧн помъясыс — сетӧм чут да вундысьлӧн кытшвизькӧд вомӧнасянін чут.

2) Унаӧн-ӧ A чутсянь r радиуса кытшвизьӧдз медыджыд ылнакостыс ыджыдджык медічӧт ылнакостысь?

3) Построитны чутъяслысь геометрическӧй местаяссӧ, кодъясӧс ылыстӧма r = 5 см радиусӧн сетӧм кытшвизьысь 2 см коласт сайӧ.

13. Мый лоӧ геометрическӧй местаӧн кытшвизьяс шӧръяслӧн, кытшвизьясыс кӧ касайтчӧны сетӧм кык веськыд визьӧ AB да CD: 1) параллельнӧйясӧ да 2) вомӧнасянаясӧ?

14. Нуӧдны r = 5 см радиуса кытшвизьын касательнӧй сідз, медым сійӧ сетӧм MN веськыдлы вӧлі перпендикулярнӧй. Исследуйтны, кымын касательнӧй позьӧ нуӧдны да ыджыд-ӧ на костын ылнакостыс.

15. O кытшвизьлы нуӧдӧма MN касательнӧй. Босьтӧма любӧй AB диаметр да A да B помъяссяньыс MN касательнӧйлы нуӧдӧма перпендикуляръяс: AC = a да BD = b. Колӧ докажитны, мый тайӧ перпендикуляръяслӧн сумма диаметр ыджда: a + b = 2r.

16. Мый лоӧ геометрическӧй местаӧн сетӧм кытшвизьын нуӧдӧм ӧтыджда хордаясса шӧръяслӧн?

XII. ПЕЛЬӦСЪЯСӦС МУРТАЛӦМ.

1 §. Кытшвизь вылын йыла пельӧс да сійӧс мурталӧм.

1. Кытшвизь шӧрчутын йыла пельӧс лоӧ центральнӧй пельӧс да муртассьӧ бокъяс костас йӧртӧм дугаӧн.

Видлалам пельӧсъяс, кодъяслӧн йывъяс куйлӧны оз кытшвизь шӧрчутын, а кытшвизь вылас, кытшвизь саяс либӧ кытшвизь пытшкас.

2. Пельӧс, кодлӧн йылыс куйлӧ кытшвизь вылын да бокъясыс — хордаяс, шусьӧ вписаннӧй пельӧсӧн.

∠ABC — вписаннӧй пельӧс (186 серп.), сійӧ сиптыссьӧ кытшвизь AC дугаӧн; AC дугалы соответствуйтӧ AOC центральнӧй пельӧс.

3. Теорема. Вписаннӧй пельӧс сійӧ жӧ дугаӧн сиптыссян центральнӧй пельӧс джын ыджда да муртассьӧ тайӧ дуга джыннас.

Сетӧма: ∠ABC — вписаннӧй пельӧс, AB да BC — хордаяс (186 серп.).

___________________________________

Колӧ докажитны: ∠ABC = ∠AOC/2.

Докажитӧм: Видзӧдлам янасӧн лоны вермана куим случай.

1) Вписаннӧй пельӧслӧн бокъясыс — BA диаметр да BC хорда (187 серп.). C чутӧс ӧтлаалам O шӧрчуткӧд; лоӧ кык ӧткузя бока ∆BCO: сы вӧсна, мый OB = OC = r; AOC центральнӧй пельӧс BOC куимпельӧсалӧн — ортсыс пельӧс, та вӧсна ∠AOC = ∠B + ∠C, но ∠B = ∠C, сідзкӧ, ∠AOC = 2∠B; татысь ∠B, либӧ ∠ABC = ∠AOC/2.

AOC центральнӧй пельӧс муртассьӧ AC дугаӧн; но вписаннӧй пельӧс центральнӧй пельӧс джын ыджда, сідзкӧ, сійӧ муртассьӧ сиптыссян дуга джыннас:

∠ABC муртассьӧ ‿AC/2.

2) ABC вписаннӧй пельӧслӧн бокъясыс — BA да BC хордаяс, кодъяс костын куйлӧ кытшвизьлӧн O шӧрчут (188 серп.).

Нуӧдам BD диаметр, коді вписаннӧй пельӧсӧс торйӧдас кык пельӧсӧ: ∠x да ∠y, а центральнӧйӧс — ∠α да ∠β-ӧ.

∠x = ∠α/2 да ∠y = ∠β/2;

сідзкӧ,

∠x + ∠y = ∠α/2 + ∠β/2 = (∠α + ∠β)/2.

Тадз,

∠ABC = ∠AOC/2; ∠ABC муртассьӧ ‿AC/2.

3) ABC вписаннӧй пельӧслӧн бокъяс — BA да BC хордаяс, кодъяс кытшвизь шӧрчутсянь кыкнаныс ӧтарланьын (189 серп.).

∠ABC = ∠CBD − ∠ABD да ∠AOC = ∠COD − ∠AOD,

но

∠CBD = ∠COD/2 да ∠ABD = ∠AOD/2,

та вӧсна

∠CBD − ∠ABD = ∠COD/2 − ∠AOD/2 = (∠COD − ∠AOD)/2.

Та ногӧн,

∠ABC = ∠AOC/2; ∠ABC муртассьӧ ‿AC/2.

Вписаннӧй пельӧслӧн ыдждаыс оз зависит сыысь, кыдз кытшвизь шӧрчут серти куйлӧны сылӧн бокъясыс, да век сійӧ жӧ дугаӧн сиптыссян центральнӧй пельӧс джын ыджда.

Следствийӧяс. I. Ӧти сійӧ жӧ дугаӧн сиптыссян вписаннӧй пельӧсъяс ӧтыдждаӧсь (190-ӧд серпас).

∠B, ∠B₁, ∠B₂, ... сиптыссьӧны ӧти сійӧ жӧ дугаӧн; на пиысь быд пельӧс муртассьӧ сійӧ джыннас; сідзкӧ найӧ ставныс мӧда-мӧдкӧд ӧтыдждаӧсь: ∠B = ∠B₁ = ∠B₂ ...

Ӧтлаалам A да C чутъясӧс AC хордаӧн. Шуӧны, мый тайӧ хорда ABC дуга вывса любӧй чутсянь тыдалӧ ӧти сійӧ жӧ пельӧс улын.

II. Диаметрӧн сиптыссян вписаннӧй пельӧс — веськыд пельӧс.

∠B = ∠B₁ = ∠B₂ = d (191 серпас) сы вӧсна, мый на пиысь быд пельӧс сиптыссьӧ 180°-а дугаӧн да муртассьӧ сійӧ джыннас, сідзкӧ, 90° ыджда.

4. Теорема. Касательнӧйӧн да касанньӧ чутсянь нуӧдӧм хордаӧн артман пельӧс муртассьӧ на костӧ йӧртӧм хорда^“хорда” пыдди колӧ гижны “дуга”. — А. В./^ джынӧн.

Сетӧма: AB — касательнӧй, AC — хорда (192-ӧд серпас).

______________________________________

Колӧ докажитны: ∠BAC муртассьӧ ‿AC/2.

Докажитӧм. Нуӧдам отсасьысь веськыдӧс CD ∥ AB. Сэк ∠α = ∠β кыдз крестӧн куйлысьяс да ‿AC = ‿AD кыдз параллельнӧйяс костын — AB касательнӧй да CD хорда костын — дугаяс.

Тадз, ∠β муртассьӧ ‿AD/2, но ∠β = ∠α да ‿AD = ‿AC, та вӧсна ∠α муртассьӧ ‿AC/2.

5. Задача. Ортсыс A чутсянь сетӧм кытшвизьлы нуӧдны касательнӧйӧс (мӧд способ) (193-ӧд серпас).

Построенньӧ. A чутӧс ӧтлаалам O шӧрчуткӧд да нуӧдам OA вылын кыдз диаметр вылын отсасьысь кытшвизь, коді сетӧм кытшвизькӧд вомӧнасяс B да B₁ чутъясын; A да B да A да B₁ чутъяс пыр нуӧдӧм веськыд визьяс — корсян AB да AB₁ касательнӧйяс. Тайӧ тадз сы вӧсна, мый ∠B да ∠B₁ веськыдӧсь кыдз C чутын шӧрчута кытшвизь OA диаметрӧн сиптыссян пельӧсъяс, та вӧсна AB ⊥ OB да AB₁ ⊥ OB₁, а OB да OB₁ сетӧм кытшвизьлӧн радиусъяс.

6. Задача. Сетӧм AB вундӧг вылӧ вӧчны сегмент сідз, медым сэтчӧ тӧрис сетӧм α пельӧс (194-ӧд серпас).

1) Решитӧм. Шуам, мый миян задача решитӧма да сетӧм AB вундӧг вылӧ кыдз хорда вылӧ вӧчӧма ACB сегмент, кытчӧ тӧрӧ ∠α. A чут пыр нуӧдам AD касательнӧйӧс; лоӧ ∠BAD = ∠ACB = α кыдз ӧти сійӧ жӧ AB дуга джынӧн муртассян пельӧсъяс. ACB сегмента круглӧн шӧрчут куйлӧ AO да OE^E — тайӧ AB вундӧглӧн шӧр. — А. В./^ перпендикуляръяс вомӧнасянін чутын.

2) Построенньӧ. Сетӧм AB вундӧг A помӧ (194 серп.) вӧчам ∠DAB = ∠α; нуӧдам AO ⊥ AD да AB вундӧг E шӧр пыр — EO ⊥ AB. AO да EO перпендикуляръяслӧн вомӧнасянін чут эм корсян кытшвизьлӧн шӧрчут. Сэсся OA радиусӧн нуӧдам кытшвизь, лоӧ корсян ACB сегмент. ACB дуга вывса любӧй чут лоӧ сетӧм α пельӧс ыджда пельӧслӧн йыв.

3) ACB дуга вывса йыла пельӧсъяс пиысь быд пельӧс муртассьӧ AB дуга джынӧн, та вӧсна найӧ ставныс сетӧм α пельӧс ыдждаӧсь.

4) Сетӧм ∠α кӧ вӧчны AB вундӧг помӧ мӧдарлань, построенньӧ сетас мӧд сегмент, коді AB вундӧг серти водзын вӧчӧм сегменткӧд лоӧ симметричнӧй.

5) Тайӧ задача решитӧмысь позьӧ вӧчны татшӧм вывод:

Кутшӧм чутъяссянь сетӧм AB вундӧг тыдалӧ сетӧм α пельӧс улын, тайӧ чутъяслӧн геометрическӧй местаӧн лоӧны AB вундӧг вылын кыдз хорда вылын вӧчӧм да сетӧм пельӧсӧс тӧрӧдысь кык симметричнӧй сегментъяслӧн дугаяс.

6) Корсяна ёсь пельӧсӧс тӧрӧдысь сегментыс ыджыдджык кругса кык сегмент пиысь, кодъяс вылӧ кругсӧ юкӧ сетӧм AB хорда.

Сетӧм β пельӧсыс кӧ тшӧтшыд, то сылӧн корсяна сегментыс лоӧ кык сегмент пиысь дзоляджыкыс, кодъяс вылӧ кругӧс юкӧ AB хорда.

Сетӧм пельӧсыс кӧ веськыд, сэк сетӧм AB вундӧг лоӧ диаметрӧн, мый вӧсна кыкнан сегментыс ӧтыдждаӧсь; сэк геометрическӧй местаӧн лоӧ кытшвизь, кодлӧн диаметрыс AB ыджда.

2 §. Пельӧс мурталӧм, кодлӧн йылыс куйлӧ круг пытшкын.

1. Теорема. Круг пытшкын йыла пельӧс муртассьӧ бокъяс костас да найӧс нюжӧдӧмъяс костас йӧртӧм дугаяс сумма джынӧн.

Сетӧма: ∠AMC — круг пытшкын йыла пельӧс (195-ӧд серпас).

_____________________________

Колӧ докажитны: ∠AMC муртассьӧ (‿AC + ‿DB)/2.

Докажитӧм. AMC пельӧслысь бокъяссӧ нюжӧдам кытшвизькӧд B да D чутъясын вомӧнасьтӧдз да нуӧдам AD хорда; лоӧ ADM куимпельӧса, кодлӧн ∠AMC — ортсыс пельӧс.

Ортсыс ∠AMC = ∠A + ∠D, но ∠A муртассьӧ ‿BD/2, ∠D муртассьӧ ‿AC/2, сідзкӧ ∠AMC = ∠A + ∠D муртассьӧ (‿AC + ‿BD)/2.

2. Круг пытшкын йыла быд пельӧс вылӧ позьӧ видзӧдны кыдз кык хорда вомӧнасьӧмысь артман пельӧсъяс пиысь ӧти пельӧс вылӧ.

Сійӧ случайын, кор хордаяслӧн вомӧнасянін чут усьӧ шӧрчутӧ, круг пытшкын йыла пельӧс ӧттшӧтш лоӧ центральнӧй пельӧсӧн; сідзкӧ, позьӧ шуны, мый центральнӧй пельӧс муртассьӧ бокъяс костас да найӧс нюжӧдӧмъяс костас йӧртӧм дугаяс сумма джынӧн.

Кор хордаяслӧн вомӧнасянін чут матысмӧ кытшвизь дінӧ, сэк хордаяс костӧ йӧртӧм дугаяс пиысь ӧтиыс ичӧтмӧ; ичӧтмӧм мунӧ нульӧдз; тадз лоӧ сэк, кор хордаяслӧн вомӧнасянін чут воас кытшвизь вылӧ. Та вӧсна хордаясӧн артмӧм пельӧс йылысь теорема лоӧ справедливӧй тшӧтш и тайӧ случайын.

3 §. Пельӧс мурталӧм, кодлӧн йылыс куйлӧ круг ортсыын.

1. Теорема. Круг сайын йыла пельӧс муртассьӧ бокъяс костас йӧртӧм дугаяс разносьт джынӧн.

Сетӧма: круг сайын йыла пельӧс; MA да MD — вундысьяс (196-ӧд серпас).

__________________________________

Колӧ докажитны: ∠M муртассьӧ (‿AD − ‿BC)/2.

Докажитӧм. Видлалам куим случай: 1) ∠M артмӧма кык вундысьӧн — MA да MD. Нуӧдам отсасьысь AC хорда; лоӧ ∆AMC, кодлӧн ∠ACD — ортсыс пельӧс; татысь петӧ, мый ∠M = ∠ACD − ∠A; но ∠ACD муртассьӧ ‿AD/2 да ∠A муртассьӧ ‿BC/2; сідзкӧ, ∠M муртассьӧ (‿AD − ‿BC)/2.

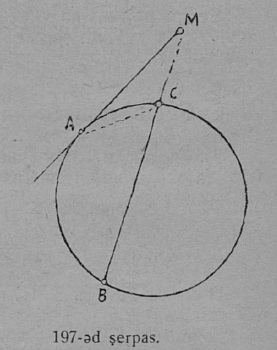
2) ∠M артмӧма MA касательнӧйӧн да MD вундысьӧн (197 серп.).

MA касательнӧй вылӧ видзӧдам кыдз вундысь вылӧ, кодлӧн кытшвизькӧд кык ӧтувъя чут ӧтлаасисны ӧти A чутӧ; та вӧсна водзын вӧчӧм кык вундысьӧн артман пельӧсӧс мурталӧм йылысь вывод лоӧ справедливӧй и тайӧ случай вылӧ: ∠M муртассьӧ (‿AB − ‿AC)/2.

Тайӧ случай позьӧ докажитны и самостоятельнӧя. Та могысь колӧ нуӧдны AC хорда (197-ӧд серпас) да видзӧдлыны ACM куимпельӧса вылӧ: ∠M = ∠ACB − ∠CAM.

3) ∠M артмӧма кык касательнӧйӧн — MA да MB (198-ӧд серпас).

Медым ME да MF вундысьяс M чут гӧгӧр бергӧдчигӧн воасны MA да MB касательнӧйяс положенньӧӧ; татшӧм случайын EF дуга содӧ ACB дугаӧдз, а E₁F₁ дуга — ADB дугаӧдз; сэк касательнӧйясӧн артман ∠M кутас муртассьыны (‿ACB − ‿ADB)/2.

Кык касательнӧйӧн артман пельӧс шусьӧ описаннӧй пельӧсӧн.

2. Круг сайын M йыла ∠AMC AC дугаӧн сиптыссян вписаннӧй ABC пельӧсысь ичӧтджык. Круг пытшкын N йыла ∠ANC сійӧ жӧ вписаннӧй пельӧсысь ыджыдджык (199-ӧд серпас).

1) ∠M муртассьӧ (‿AC − ‿KL)/2;

2) ∠B муртассьӧ ‿AC/2;

3) ∠N муртассьӧ (‿AC + ‿A₁C₁)/2;

4) (‿AC − ‿KL)/2 < ‿AC/2; ‿AC/2 < (‿AC + ‿A₁C₁)/2,

та вӧсна

∠M < ∠B < ∠N.

Юасянъяс да упражненньӧяс.

1. ABC куимпельӧсалӧн йывъяс куйлӧны кытшвизь вылын. Определитны сылысь пельӧсъяссӧ, кор тӧдам, мый ‿AB = 70° да ‿BC = 60°.

2. Кытшвизьӧс юкӧма 5 : 8 : 11 отношенньӧын. Юкан чутъясыс — куимпельӧсалӧн йывъяс. Определитны куимпельӧсалысь пельӧсъяссӧ.

3. Сетӧма ∠ABC = α. Вӧчны кытшвизь отсӧгӧн пельӧс, медым сійӧ вӧлі 1) сетӧм пельӧс джын ыджда; 2) кык сетӧм пельӧс ыджда.

4. Кык вписаннӧй B да B₁ пельӧсъяслӧн бокъясыс параллельнӧйӧсь (200-ӧд серпас). Докажитны, мый ‿AC = ‿A₁C₁.

5. Артавны, кутшӧм ёсь пельӧс улын кругын вомӧнасьӧны AB да CD хордаяс, кор A, B, C да D чутъяс кытшвизьӧс юкӧны 2 : 3 : 6 : 7 отношенньӧын.

6. Кык радиус костса пельӧс 110° ыджда. Определитны тайӧ радиусъяс помъяс пыр нуӧдӧм касательнӧйясӧн артман пельӧс.

XIII. КЫК КЫТШВИЗЬЛӦН ОТНОСИТЕЛЬНӦЙ ПОЛОЖЕННЬӦ.

1 §. Концентрическӧй да эксцентрическӧй кытшвизьяс.

1. Кык кытшвизьлӧн вермасны лоны либӧ ӧтувъя шӧрчут либӧ разнӧй шӧрчутъяс. Ӧтувъя шӧрчута кык кытшвизь шусьӧны концентрическӧйясӧн. Мӧда-мӧдысь найӧ торйӧдчӧны R да r радиусъяс кузьтананыс (201 серп.).

Кык концентрическӧй кытшвизь костса плоскосьтлӧн юкӧн шусьӧ кытшвизьса кольцоӧн. Концентрическӧй кытшвизьясса радиусъяслӧн разносьт (R − r) определяйтӧ круговӧй кольцолысь пасьта.

Разнӧй шӧрчута кык кытшвизь шусьӧны эксцентрическӧйясӧн.

2. Кык кытшвизьса шӧрчутъяс пыр мунысь OO₁ веськыд (202 серп.) шусьӧ шӧрчутъяс визьӧн.

Кык кытшвизьлӧн шӧрчутъяс визьыс лоӧ налӧн симметрия ось.

OO₁ вундӧг = d лоӧ O да O₁ шӧрчутъяс костса расстоянньӧӧн, кодӧс дженьдӧдӧм вылӧ унджыкыс шуӧны сідзжӧ шӧрчутъяс визьӧн.

Концентрическӧй кытшвизьясын шӧрчутъяслӧн визьыс нуль ыджда.

3. Кытшвизьяс, кодъяслӧн мӧда-мӧдкӧд эм сӧмын ӧти ӧтувъя чут, шусьӧны касательнӧйясӧн. Налӧн ӧтувъя чут шусьӧ касанньӧ чутӧн либӧ прикосновенньӧ чутӧн.

Кор кык кытшвизь касайтчӧны да ӧти кытшвизьыс мӧдыс сайын, сэк шуӧны, мый налӧн ортсыс касанньӧ; кор мӧда-мӧдкӧд касайтчан кык кытшвизь пиысь ӧтиыс мӧдыс пытшкын, сэк шуӧны, мый налӧн пытшкӧс касанньӧ.

Кытшвизьяс, кодъяслӧн эм кык ӧтувъя чут, вомӧнасьӧны; вомӧнасянін чутъясӧс ӧтлаалысь веськыд визь лоӧ налӧн ӧтувъя хорда.

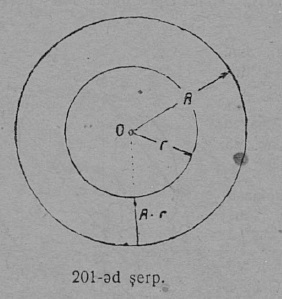
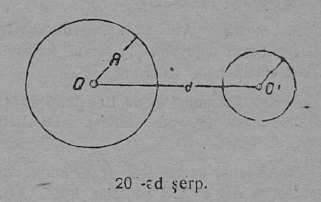
Кытшвизьяс, кодъяслӧн эм куим ӧтувъя чут, ӧтлаасьӧны.

Техникаын касательнӧй кругъясӧс используйтӧны фрикционнӧй да пиня кӧльӧсаясӧн движенньӧяс передайтӧм вылӧ. Ортсыс касанньӧ дырйи фрикционнӧй да пиня кӧльӧсаяс бергалӧны мӧда-мӧдлы воча направленньӧын, а пытшкӧс касанньӧ дырйи — ӧти сійӧ жӧ направленньӧын.

2 §. Кык кытшвизьлӧн мӧда-мӧдкӧд положенньӧ.

1. Теорема. Кык разнӧй кытшвизьлӧн кӧ эм ӧтувъя чут, коді куйлӧ найӧ шӧрчутъяс визьсянь ӧтарбокын, сэк налӧн эм и мӧд ӧтувъя чут, коді куйлӧ найӧ шӧрчутъяс визьсянь мӧдарбокас, либӧ мӧд ног кӧ, тайӧ кытшвизьясыс вомӧнасьӧны (203 серп.).

Збыльысь ӧд, шӧрчутъясныслӧн визьыс — кыкнан кытшвизьыслӧн симметрия ось. Пуктам A чутлы симметричнӧй B чут да ӧтлаалам сійӧс кытшвизьясса O да O₁ шӧрчутъяскӧд; сэк симметрия серти OA = OB да O₁A = O₁B, та вӧсна B лоӧ кыкнан кытшвизьыслӧн чут, кытшвизьясыс вомӧнасьӧны, да AB — налӧн ӧтувъя хорда.

Следствийӧ. Кык разнӧй кытшвизьлӧн кӧ ӧтувъя A чутныс куйлӧ шӧрчутъясса визь вылын, сэк кытшвизьясыс касайтчӧны, либӧ мӧд ног кӧ, налӧн эм сӧмын ӧти ӧтувъя A чут, коді куйлӧ шӧрчутъясса визьныс вылын.

Збыльысь ӧд, босьтны кӧ намӧдар, мый тайӧ кык кытшвизьлӧн эм нӧшта мӧд ӧтувъя чут, коді оз куйлы шӧрчутъясса визьныс вылын, сэк докажитӧм теорема серти налӧн колӧ лоны нӧшта коймӧд ӧтувъя чут, шӧрчутъясса визьныс серти мӧд чутыслы симметричнӧй; сэк тайӧ кытшвизьяслӧн колӧ лоны куим ӧтувъя чут, но тайӧ оз вермы лоны сы вӧсна, мый 3 ӧтувъя чута кытшвизьяс вевсяасьӧны, а тайӧ оз нин лӧсяв условийӧлы. Сідзкӧ,

кык кытшвизь касайтчӧны, кор налӧн эм ӧти ӧтувъя чут, коді куйлӧ шӧрчутъясса визь вылын (204 да 205 серп.).

2. Сетӧма кык кытшвизь, кодъяслӧн разнӧй R да r радиусъяс. Кытшвизьяс оз касайтчыны да куйлӧны мӧда-мӧд сайын. R радиуса кытшвизьӧс кӧ эновтны вӧрзьытӧг, а r радиуса кытшвизьлысь шӧрчут кӧ новлӧдлыны шӧрчутъяс визь кузяыс, кытшвизьяслӧн мӧда-мӧдыскӧд вермасны лоны разнӧй положенньӧяс.

1. Кытшвизьяс оз вомӧнасьны, оз касайтчыны, ӧтиыс куйлӧ мӧд сайын (202 серп.). Сэк найӧ шӧрчутъяс костса OO₁ = d расстоянньӧ найӧ радиусъяс суммаысь ыджыдджык: d > R + r.

2. Кытшвизьяслӧн A чутын ортсыс касанньӧ (204 серп.). Сэк OO₁ = d расстоянньӧ найӧ радиусъяс сумма ыджда: d = R + r.

3. Кытшвизьяс вомӧнасьӧны; налӧн ӧтувъя чутъяс A да B (203 серп.). OO₁ = d да R да r радиусъяс костысь зависимосьт корсьӧм вылӧ видлалам AOO₁ куимпельӧсаӧс, кӧн OO₁ = d, AO = R да AO₁ = r. Куимпельӧсаын любӧй бок 1) мӧд кык бок суммаысь ичӧтджык, 2) мӧд кык бок разносьтысь ыджыдджык; та вӧсна шӧрчутъяс костса расстоянньӧ кытшвизьяс радиусъяс суммаысь ичӧтджык да найӧ разносьтысь ыджыдджык: d < R + r да d > R − r.

4. Кытшвизьяслӧн пытшкӧс касанньӧ (205 серп.). Шӧрчутъяс костса расстоянньӧ OO₁ = d радиусъяс разносьт ыджда: d = R − r.

5. Ӧти кытшвизь куйлӧ мӧдыс пытшкын да налӧн шӧрчутъяс абу ӧтлаын (206 серп.). OO₁ = d расстоянньӧ радиусъяс разносьтысь ичӧтджык: d < R − r.

6. Ӧти кытшвизь куйлӧ мӧдыс пытшкын, шӧрчутъяс налӧн ӧтлаын (207 серп.). Шӧрчутъяс костса расстоянньӧ нуль ыджда: d = 0.

3 §. Кык вомӧнасян кытшвизьса ӧтувъя хордалӧн свойство.

Теорема. Кык вомӧнасян кытшвизьлӧн ӧтувъя хорда шӧрчутъяс визьлы перпендикулярнӧй да сійӧн юксьӧ шӧри.

Сетӧма: O кытшвизь да O₁ кытшвизь (203, 208 серп.).

AB — ӧтувъя хорда; OO₁ — шӧрчутъяс визь.

_________________________________

Колӧ докажитны: 1) AB ⊥ OO₁ да 2) AC = CB.

Докажитӧм. Кытшвизьяслысь вомӧнасянін A да B чутъяссӧ ӧтлаалам O да O₁ шӧрчутъяскӧд; лоӧны кык ӧткузя бока куимпельӧсаяс — AOB да AO₁B — да кык ӧтыджда куимпельӧса — AOO₁ да BOO₁, кодъяслӧн OO₁ — ӧтувъя бок, OA = OB = R да O₁A = O₁B = r.

Куимпельӧсаяс равенствоысь петӧ пельӧсъяслӧн равенство: 1) ∠AOO₁ = ∠BOO₁ да 2) ∠AO₁O = ∠BO₁O; сідзкӧ, OO₁ — ∠O да ∠O₁-лӧн биссектриса.

Кык ӧткузя бока AOB да AO₁B куимпельӧсаясын OO₁ шӧрчут визь лоӧ биссектрисаӧн; та вӧсна: 1) AB ⊥ OO₁ да 2) AC = CB.

4 §. Кык кытшвизь бердса ӧтувъя касательнӧйяс да найӧс вӧчӧм.

I. Кымын ӧтувъя касательнӧйӧс позьӧ нуӧдны кык кытшвизь бердӧ, тайӧтор зависитӧ сыысь, кутшӧмджык кытшвизьясыслӧн мӧда-мӧдыскӧд положенньӧыс. І — ІV серпас вылын (209-ӧд серпас) мыччӧдӧма став случай, кутшӧмъяс вермасны лоны кык кытшвизь бердӧ ӧтувъя касательнӧйясӧс нуӧдігӧн.

Татчӧ вайӧдан табличаын индыссьӧ кык кытшвизь шӧрчутъяс костса расстоянньӧяслӧн да найӧ касательнӧйяс лыдлӧн зависимосьт, коді лоӧ кык кытшвизьлӧн мӧда-мӧдыскӧд торъя положенньӧяс дырйи.

Пӧрадок №№	d — кык кытшвизь шӧрчутъяс костса расстоянньӧ	Кык кытшвизьлӧн мӧда-мӧдкӧд положенньӧ	Касательнӧйяслӧн лыд
1	d > R + r	Кытшвизьяс оз вомӧнасьны, оз касайтчыны да ӧтиыс куйлӧ мӧдыс сайын	4
2	d = R + r	Кытшвизьяслӧн ортсыс касанньӧ	3
3	d < R + r, d > R − r	Кытшвизьяс вомӧнасьӧны	2
4	d = R − r	Кытшвизьяслӧн пытшкӧс касанньӧ	1
5	d < R − r	Ӧти кытшвизьыс куйлӧ мӧдыс пытшкын; налӧн шӧрчутъяс абу ӧтлаын	0
6	d = 0	Ӧти кытшвизь куйлӧ мӧдыс пытшкын; налӧн шӧрчутъяс ӧтлаын	0

2. Задача. Разнӧй радиусъяса, R да r, кык кытшвизь бердӧ вӧчны ӧтувъя касательнӧйясӧс, кор d > R + r.

Видзӧдлам кык сетӧм кытшвизь серти касательнӧйяс положенньӧяслысь лоны вермана кык случай.

1) Построенньӧ. Нуӧдам (R − r) ыджда радиусӧн сетӧм кытшвизьяс пиысь ыджыдджыкыскӧд концентрическӧй отсасьысь кытшвизь (210 серп.) да сы бердӧ O₁ шӧрчутысь — O₁C касательнӧйӧс. C касанньӧ чут пыр нуӧдам OC радиус да нюжӧдам сійӧс сетӧм кытшвизьыскӧд A чутын вомӧнасьтӧдз; O₁ шӧрчутысь нуӧдам O₁B ∥ OA; A да B чутъясӧс ӧтлаалам AB веськыдӧн; AB веськыд — корсян касательнӧй. Татшӧм жӧ построенньӧӧн артмӧ A₁B₁ касательнӧй.

Докажитӧм. CA = O₁B да CA ∥ O₁B построенньӧ серти; таысь ӧтдор, ∠C = d; сідзкӧ, ABO₁C нёльпельӧса — веськыднёльпельӧса, та вӧсна ∠A да ∠B — веськыд пельӧсъяс; та ногӧн OA да O₁B радиусъяс, кодъясӧс нуӧдӧма касанньӧ чутъясӧ, AB веськыдкӧд вӧчӧны веськыд пельӧсъяс; сідзкӧ, AB — ӧтувъя касательнӧй кыкнан кытшвизь бердӧ.

2) Построенньӧ. Нуӧдам (R + r) ыджда радиусӧн кытшвизь, коді мед вӧлі сетӧм кытшвизьяс пиысь ыджыдджыкыслы концентрическӧй (211-ӧд серпас). Тайӧ кытшвизьыс бердӧ нуӧдам O₁C касательнӧйӧс; C касанньӧ чут пыр нуӧдам OC радиус, коді сетӧм кытшвизьысӧс вундас A чутын; сэсся O₁ шӧрчутысь нуӧдам радиус O₁B ∥ OC; A да B чутъясӧс ӧтлаалӧм бӧрын сюрӧ корсян AB касательнӧй.

Татшӧм жӧ построенньӧӧн артмӧ мӧд ӧтувъя A₁B₁ касательнӧй.

Докажитӧм. CA = O₁B да CA ∥ O₁B построенньӧ серти; таысь ӧтдор, ∠C = d; мый вӧсна ABO₁C нёльпельӧса — веськыдпельӧса; ∠A да ∠B — веськыд пельӧсъяс; сідзкӧ O₁B да OA радиусъяс, кодъясӧс нуӧдӧма A да B чутъясӧ, AB веськыдлы перпендикулярнӧйӧсь, кытысь петӧ, мый AB — кыкнан кытшвизь бердӧ ӧтувъя касательнӧй.

Воддза случайын касательнӧйяс шусьӧны ортсысса касательнӧйясӧн, а мӧдын — пытшкӧсса касательнӧйясӧн.

3. Ортсысса да пытшкӧсса касательнӧйяс паныдасьӧны шкивъяс кост тасмаа передача дырйи (212 серп.). Помтӧм тасма кӧ мунӧ ортсыс касательнӧйяс кузя, шкивъяс бергалӧны ӧти направленньӧӧн; тасма кӧ мунӧ пытшкӧс касательнӧйяс кузя, шкивъяс бергалӧны воча направленньӧӧн.

Юасянъяс да упражненньӧяс.

1. Кыдзи нуӧдны ӧтувъя касательнӧйясӧс ӧтыджда радиусъяса кык кытшвизь бердӧ?

2. Сетӧма R = 6 см радиуса кытшвизь. Мый лоӧ r = 2 см радиусъяса кытшвизьяс шӧрчутъяслӧн геометрическӧй местаыс, радиусъясыс^кытшвизьясыс?/^ кор касайтчӧны сетӧм кытшвизяс? Кутшӧм случайяс вермасны лоны?

3. Нуӧдны 8 см да 5 см радиусъяса кык концентрическӧй кытшвизь, сэсся вӧчны некымын кытшвизь сідз, медым найӧ касайтчисны кыкнан кытшвизяс. Ыджыдӧсь-ӧ радиусъяс выльӧн вӧчӧм кытшвизьяслӧн? Мый ыджда круговӧй кольцолӧн пасьта?

4. Докажитны, мый кык неӧтыджда кытшвизь бердӧ ӧтувъя пытшкӧс (либӧ ортсыс) касательнӧйяс ӧтыдждаӧсь да вомӧнасьӧны шӧрчутъяс визь вылын.

5. Докажитны, мый кык кытшвизь ортсыс касанньӧ дырйи ӧтувъя ортсыс касательнӧйяс да на костӧ йӧртӧм ӧтувъя пытшкӧс касательнӧйлӧн вундӧг ӧтыдждаӧсь.

XIV. ГЕОМЕТРИЧЕСКӦЙ МЕСТАЯС МЕТОДӦН ПОСТРОЕННЬӦ ВЫЛӦ ЗАДАЧАЯС.

1 §. Построенньӧ вылӧ задачаясӧс видлалӧм.

1. Построенньӧ вылӧ задача тшӧктӧ циркуль да линейка отсӧгӧн вӧчны геометрическӧй фигураӧс, коді мед кутіс задача условийӧын индӧм определённӧй свойствояс.

Построенньӧ вылӧ задачаӧс сполнӧя решитӧм артмӧ нёль юкӧнысь: 1) анализысь, либӧ разборысь, да, сідзкӧ, задача решитӧм вылӧ план вӧчӧмысь; 2) построенньӧсӧ вӧчӧмысь; 3) докажитӧмысь, мый вӧчӧм фигураыс задачаса став условийӧяскӧд ладмӧ; 4) условийӧяссӧ исследуйтӧмысь, кор задачасӧ решитны позьӧ да кымын ногӧн.

2. Задача 1. Вӧчны куимпельӧсаӧс, кор сылысь сетӧма a бок, сы бердса B пельӧс да b бок, коді куйлӧ B пельӧс водзын (213 серп.).

Решитӧм. 1) Задачалӧн анализ. Ми кужам, кыдз вӧчны B пельӧс куимпельӧсаса бок ыджда BC вундӧг помӧ: ми тӧдам куимпельӧсалысь кык йыв — B да C — да ∠B. Коймӧд A йывлы колӧ куйлыны B пельӧс BA бок вылын да C чутын шӧрчута AC = b бок ыджда радиуса кытшвизь вылын.

2) Построенньӧ. MN веськыд визь вылӧ пуктам a ыджда BC вундӧг да B помас вӧчам B пельӧс. Сэсся нуӧдам b ыджда радиусӧн C чутын шӧрчута кытшвизь, коді B пельӧслысь BA боксӧ вундас A да A₁ чутъясын. Та ногӧн A йывлӧн сюрӧ кык положенньӧ: A да A₁. Сідзкӧ, лоӧны кык куимпельӧса: ABC да A₁BC.

3) Докажитӧм. Кыкнан куимпельӧсаыс задача условийӧяслы удовлетворяйтӧны.

4) Исследуйтӧм. B пельӧс BA боклы C чутсянь нуӧдам CA₂ перпендикуляр. C чутын шӧрчута кытшвизь, кор сылӧн радиус CA₂ ыджда, кутас касайтчыны BA бокӧ; сэк лоӧ сӧмын ӧти решенньӧ; та дырйи b < a. BA бокӧс кытшвизь вермас вундыны кык чутын — A да A₁ (кор b < a); сэк лоӧ кык решенньӧ:

1) ∆ABC, сылӧн бокъяс: a, b да AB = c, пельӧсъяс: B, BAC да ACB;

2) ∆A₁BC, сылӧн бокъяс: a, b да A₁B = c₁, пельӧсъяс: B, BA₁C = 180° − A; сы вӧсна, мый ∠A = ∠AA₁C (кык ӧткузя бока куимпельӧсаын подувтас бердса пельӧсъяс; тайӧ куимпельӧсаын ∠A₁CB = ∠A − ∠B). Кор b = a, лоӧ сӧмын ӧти решенньӧ, а корсян куимпельӧса лоӧ кык ӧткузя бока. Кор b > a, кытшвизь BA бокӧс вундас ӧти A₃ чутын; корсян куимпельӧса лоӧ A₃BC.

Если кӧ b < CA₂, мӧд ног кӧ шуны, кор b ичӧтджык B пельӧсса BA боксянь C чутӧдз коластысь, сэк кытшвизь оз каснитчы BA бокӧ дай оз вомӧнав сійӧс, сы вӧсна тайӧ случайын оз ло ньӧти решитӧм.

Задача 2. Вӧчны куимпельӧса, кор сылысь сетӧма a подувтас, m_a медиана да подувтаслы воча куйлысь ∠A = α (214 серп.).^Тані пельӧсыс ёсь. — А. В./^

Решитӧм. Задача анализ. Шуам, медым задача решитӧма да ∆ABC вӧчӧма. AD — сылӧн медиана, BC — подувтас. Сетӧм BC = a подувтас ABC куимпельӧсалысь определяйтӧ кык йыв — B да C. Коймӧд A йывсянь сетӧм BC = a подувтас тыдалӧ сетӧм α пельӧс улын. Чутъяслӧн, кодъяссянь сетӧм BC вундӧг тыдалӧ сетӧм α пельӧс улын, геометрическӧй местаӧн лоӧ сетӧм BC = a вундӧг вылын вӧчӧм да сетӧм α пельӧсӧс тӧрӧдысь BAC сегментлӧн дуга. Та ногӧн A чутлы колӧ куйлыны BAC сегмент дуга вылын. A йылӧдз BC подувтас D шӧрсянь расстоянньӧ AD = m_a ыджда. D чутсянь ӧтылнаӧ ылысмӧдӧм чутъяслӧн геометрическӧй местаӧн лоӧ D чутын шӧрчута AD = m_a радиусӧн нуӧдӧм кытшвизь. Та ногӧн, A чутлы колӧ куйлыны тайӧ кытшвизь вылын. Тадз, A чутлы, ∆ABC коймӧд йывлы, колӧ куйлыны кыкнан геометрическӧй места вылын: BAC сегмент дуга вылын да D чутын шӧрчута кытшвизь вылын; A йыв — тайӧ геометрическӧй местаяслӧн вомӧнасянін чут.

Построенньӧ. Сетӧм BC = a вундӧг вылӧ кыдз хорда вылӧ вӧчам сетӧм ∠A = α тӧрӧдысь BAC сегмент. Сэсся нуӧдам сетӧм m_a медиана ыджда радиусӧн D чутын — BC вундӧг шӧрын — шӧрчута кытшвизь. BAC сегмент дугалӧн да m_a радиуса кытшвизьлӧн вомӧнасянін чут — куимпельӧсалӧн коймӧд йыв — A. Ӧтлаалам C да B чутъясӧс A-кӧд, лоӧ корсян ABC куимпельӧса.

Докажитӧм. Вӧчӧм ∆ABC задачаса условийӧлы удовлетворяйтӧ: BC = a — сылӧн подувтас, ∠BAC = α да AD = m_a.

Исследуйтӧм. A чут лоӧ кытшвизьлӧн да сегмент дугалӧн вомӧнасянін чут, та вӧсна колӧ видзӧдлыны, век-ӧ сетӧм условийӧяс дырйи кытшвизьяс вомӧнасясны.

Сы бӧрын, кор лоӧ вӧчӧма BAC сегмент дуга, ми нуӧдам DA = m_a радиусӧн D чутын шӧрчута кытшвизь (214 серп.); та дырйи вермасны лоны куим случай: 1) кытшвизь да сегментлӧн дуга касайтчӧны A₂ чутын — налӧн эм сӧмын ӧти ӧтувъя чут; сідзкӧ позьӧ вӧчны сӧмын ӧти ∆A₂BC, коді лоӧ кык ӧткузя бока, да A₂D медиана — сылӧн судта; 2) сетӧм m_a медиана кӧ A₂D-ысь ичӧтджык, но ыджыдджык BD-ысь, то кытшвизь да сегментлӧн дуга вомӧнасясны кык чутын — A да A₁ чутъясын, лоӧны ӧтыджда кык куимпельӧса: ABC да A₁BC; 3) сетӧм m_a медиана кӧ A₂D-ысь ыджыдджык, кытшвизьяс оз вомӧнасьны, та вӧсна куимпельӧсаӧс вӧчны оз позь: задачалӧн решенньӧ абу.

Колӧ индыны, мый и BC мӧдарбокын позьӧ вӧчны сегмент, коді тӧрӧдас ∠α, да куимпельӧсаӧс, коді лоас сетӧмаыслы симметричнӧй.

Задача 3. Корсьны чут, кодӧс ӧтылнаӧ ылысмӧдӧма ABC куимпельӧсаса AB, AC да CB бокъяссянь (215 серп.).

Решитӧм. AB да AC артмӧдӧны A чут бердын паныда кык гоз пельӧс. Куимпельӧса бокъясысь ӧтылнаӧ ылысмӧдӧм чут куйлӧ ӧти пельӧс гозса ӧтувъя биссектриса вылын, либӧ мӧд пельӧс гоз биссектриса вылын. Водзын сувтлам сетӧм куимпельӧсаса A пытшкӧс пельӧс биссектриса вылын.

Нуӧдам AA₁ биссектриса, код вылын колӧ куйлыны корсян чутлы; сэсся нуӧдам B пельӧсын BB₁ биссектриса, код вылын колӧ куйлыны BA да BC бокъяссянь ӧтылнаӧ ылысмӧдӧм корсян чутлы. Корсян чут ӧттшӧтш куйлӧ кыкнан биссектриса вылын; сідзкӧ корсян чут — налӧн вомӧнасянін O чут.

Биссектриса свойство серти OM = ON да OM = OK, кытысь ON = OK.

Куимпельӧсаса бокъяссянь ӧтылнаӧ ылысмӧдӧм чут куйлӧ куимпельӧса пытшкын да вевсяасьӧ любӧй кык биссектриса вомӧнасянін чуткӧд.

C чут ӧтлаалам O чуткӧд; сы вӧсна, мый веськыдпельӧса CON да COK куимпельӧсаясын OC — ӧтувъя гипотенуза да докажитӧм серти ON = OK, тайӧ куимпельӧсаяс ӧтыдждаӧсь, кытысь: ∠OCN = ∠OCK, а тайӧ лоӧ, мый CO веськыдӧн ∠C юксьӧ шӧри, мый вӧсна CO — биссектриса. Та ногӧн, коймӧд CO биссектриса мунӧ O чут пыр.

Куимпельӧсалӧн биссектрисаяс вомӧнасьӧны ӧти чутын.

ABC куимпельӧсаса бокъяссянь ӧтылнаӧ ылысмӧдӧм O чут кындзи эм нӧшта куим чут, кодъяс кутӧны сійӧ жӧ свойство.

Збыльысь ӧд, нюжӧдны кӧ, шуам, B да C пельӧсъяслысь бокъяс да куимпельӧсаас артмӧм ортсыс кык гоз пельӧсъяслысь нуӧдны кӧ биссектрисаяс, то налӧн вомӧнасян чутыс, O₁ чут, лоӧ ӧтылнаын BC боксянь да AB да AC бокъяс нюжӧдӧмъяссянь.

Татшӧм сяма построенньӧӧн жӧ тӧдмавсьӧны, кыдзи тыдалӧ 215 серп. вылын, нӧшта кык чут — O₂ да O₃.

2 §. Задачаяс.

1. Сетӧма кык чут — A да B. Корсьны коймӧд сэтшӧм C чут, медым сійӧ вӧлі A-сянь a расстоянньӧ ылнаын, а B-сянь b расстоянньӧ ылнаын.

2. Нуӧдны кытшвизь сідз, медым сійӧ муніс сетӧм A чут пыр да медым сетӧм MN веськыд вылын босьтӧм B чутӧ касайтчис.

3. Вӧчны куимпельӧса, кор сетӧма сылысь a бок да h_b да h_c судтаяс.

4. Вӧчны куимпельӧса, кор сетӧма a подувтас, h_a судта да ∠A.

5. Корсьны геометрическӧй места: 1) сетӧм кытшвизь вывса ӧти сійӧ жӧ чутысь петан став хордаяс шӧръяслысь; 2) круг пытшкӧсса ӧти сійӧ жӧ чут пыр мунысь став хордаяс шӧръяслысь.

XV. ПРОПОРЦИОНАЛЬНӦЙ ВУНДӦГЪЯС.

1 §. Кык вундӧглӧн ӧтувъя мера.

Сетӧм кык вундӧглӧн ӧтувъя мераӧн шусьӧ сэтшӧм вундӧг, кодӧс позьӧ кыкнан сетӧм вундӧгас пуктыны быдса лыд пӧв.

Сетӧма кык вундӧг — AB да CD (216-ӧд серпас); a вундӧг AB вундӧгӧ тӧрӧ 5-ысь, а CD вундӧгӧ — 3-ысь:

AB = 5a да CD = 3a;

a эм AB да CD сетӧм вундӧгъяслӧн ӧтувъя мера. Кык вундӧглы ӧтувъя мералӧн быд юкӧн, пример вылӧ, 1/2, 1/3, 1/5, ... 1/10 ..., сідзжӧ лоӧ налы ӧтувъя мераӧн; тайӧ сы вӧсна, мый быд татшӧм юкӧн быд сетӧм вундӧгӧ пуктыссяс быдса лыдысь; татысь петӧ, мый кык вундӧглӧн вермас лоны помтӧм уна ӧтувъя мера, кодъяс пиысь ӧти медся ыджыд.

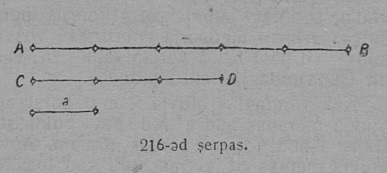
Кык вундӧг, кодъяслӧн эм ӧтувъя мера, коді (тайӧ мераыс) быд вундӧгӧ пуктыссьӧ быдса лыд пӧв, шусьӧны муртассяна вундӧгъясӧн.

Задача. Муртассяна кык вундӧглысь корсьны ӧтувъя мерасӧ.

Сетӧма кык вундӧг, AB да CD, такӧд тшӧтш AB > CD (217-ӧд серпас).

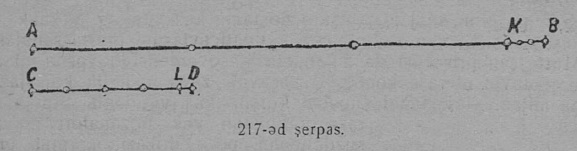
Решитӧм. Пукталам AB ыджыдджык вундӧгыс вылӧ некымын пӧв ичӧтджык CD вундӧг. Шуам, сійӧ пуктыссьӧ AB вылӧ куим пӧв да кольӧ вундӧг KB < CD. Тадзнад артмӧ:

AB = 3CD + KB. (1)

CD вундӧг кӧ AB вундӧг вылӧ пуктыссис буретш куим пӧв, то CD вундӧг эськӧ лои ӧтувъя мераӧн кыкнан вундӧгыслы да AB вундӧгӧ эськӧ тӧрис куим пӧв, а CD вундӧгӧ — ӧтиысь.

Мед сэсся KB вундӧг, медводдза колясыс, CD вундӧгӧ пуктыссьӧ нёль пӧв да, таысь кындзи, лоӧ коляс LD < KB, сэк

CD = 4KB + LD. (2)

Водзӧ пукталам LD вундӧгӧс, мӧд коляссӧ, KB вундӧг вылӧ; мед LD вундӧгыс KB вундӧг вылӧ пуктыссьӧ буретш куим пӧв, сэк

KB = 3LD, (3)

и LD лоӧ кыкнан вундӧгыслы ӧтувъя мераӧн.

(3) равенствоысь KB значенньӧсӧ (2) равенствоӧ пуктӧмӧн (подстановка вӧчӧмӧн), а сэсся CD значенньӧӧс (1) равенствоӧ пуктӧмӧн, лоас:

CD = 4∙3 LD + LD = 13 LD,

AB = 3∙13 LD + 3 LD = 42 LD.

Тадз, AB = 42 LD да CD = 13 LD; сідзкӧ, LD лоӧ ӧтувъя мераӧн AB да CD вундӧгъяслы.

LD вундӧг кӧ эськӧ эз быдса лыд пӧв пуктыссьы KB вундӧг вылын, сэк эськӧ ӧтувъя мера корсян операциясӧ лоӧ нюжӧдны сэтчӧдз, кытчӧдз артман медбӧръя колясыс сы водзвывса колясас оз пуктыссьы быдса лыд пӧв; тадзсӧ вермӧ лоны сы вӧсна, мый условийӧ серти AB да CD вундӧгъяс муртассянаӧсь.

Кык вундӧглысь ӧтувъя мера корсигӧн ми казялам, мый налӧн ӧтувъя мераныс быдса лыд пӧв пуктыссьӧ кыдзи асьныс вундӧгъясас, сідз жӧ и быд колясас, кодъяс артмӧны ӧтувъя мерасӧ корсигӧн, сідзкӧ, ӧтувъя мераыс оз вермы лоны быд лоан колясысь ыджыдджыкӧн.

Но вермасны сюрны сэтшӧм кык вундӧг, кодъяслӧн абу ӧтувъя мераныс; вундӧгъяс, кодъяслӧн ӧтувъя мераныс абу, шусьӧны муртассьытӧмъясӧн.

Колӧ пасйыны, мый кутшӧмсюрӧ босьтӧм кык вундӧг векджык абу муртассянаӧсь. Сӧмын зэв нин шоча удайтчывласны муртассянаясӧн.

Муртассян приборъяс да миян син несовершенство вӧсна ми огӧ вермӧй ӧтувъя мерасӧ корсигӧн казявны зэв посньыдик колясъяс, та вӧсна миянлы лӧсялана точносьтӧн корсьны кык вундӧглы ӧтувъя мерасӧ практикаын век позянатор; но рассужденньӧӧн позьӧ докажитны, мый эмӧсь муртассьытӧм вундӧгъяс.

Пример. Квадратлӧн бокыс да диагональыс муртассьытӧмӧсь.

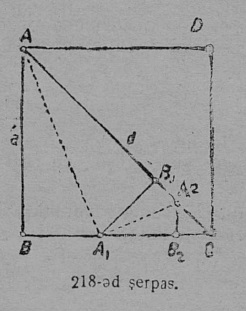
Сетӧма ABCD квадрат, кодлӧн бокыс a ыджда да диагональыс d ыджда (218 серп.).

Кык ӧткузя бока веськыдпельӧса ABC куимпельӧсаысь петӧ, мый

a < d < 2a.

AB = a пуктыссьӧ AC = d диагональӧ ӧти пӧв да лоӧ коляс B₁C = a₁, тадзнас,

d = a + a₁.

Нуӧдам B₁A₁ ⊥ AC да ӧтлаалам A да A₁, лоас A₁B₁ = A₁B; куимпельӧса A₁B₁C — веськыдпельӧса дай ӧткузя бокъяса, тадзсӧ сы вӧсна, мый ∠С = 45°. A₁B₁C куимпельӧсаысь петӧ, мый

B₁C = a₁ = B₁A₁ = BA₁.

B₁C = a₁ коляс пуктыссьӧ BC = a-ӧ кык пӧв, тадзсӧ сы вӧсна, мый BA₁ = a₁ да a₁ < A₁C < 2a₁, да, таысь кындзи, лоӧ коляс B₂C = a₂. Тадзнад,

a = 2a₁ + a₂.

A₂B₂C куимпельӧса тшӧтш жӧ веськыдпельӧса да кык ӧткузя бокъяса, та вӧсна сійӧ жӧ рассужденньӧясӧн пӧльзуйтчӧмӧн миян лоӧ:

a₁ = 2a₂ + a₃ да с. в.

Тадзнад артмӧ, мый ни ӧти коляс оз пуктыссьы быдса лыд пӧв ас водзвывса колясас, та вӧсна a да d вундӧгъяс абу муртассянаяс.

2 §. Вундӧгъяслӧн отношенньӧ.

1. Вундӧг мурталӧмыд лоӧ сылысь отношенньӧсӧ мӧд вундӧг дорӧ корсьӧм, кодӧс босьтӧма мера единица пыдди; вундӧгӧс мурталӧм результатын лоӧ лыд, коді мыччӧдлӧ, кымын пӧв мера единица пыдди босьтӧм вундӧгыс пуктыссьӧ мурталан вундӧгӧ.

Сідз, a вундӧг кӧ босьтны мера единица пыдди (216 серпас), AB вундӧгӧс мурталысь лыд лоӧ 5; CD вундӧгӧс мурталысь лыд лоӧ 3; гӧгӧрвоана, мый a вундӧгӧс мурталысь лыд лоӧ 1.

2. Кык вундӧгӧс, кыдзи и кык лыдӧс, позьӧ ӧтлааститны кык ногӧн. Позьӧ тӧдмавны, унаӧн-ӧ ӧти вундӧгыс ыджыдджык либӧ ичӧтджык мӧдысь, либӧ тӧдмавны, кымын пӧв ӧти вундӧгыс ыджыдджык либӧ ичӧтджык мӧдысь, мӧд ногӧн — тӧдмавны, кымынысь ӧти вундӧгыс тӧрӧ мӧдас.

Бӧръя способӧн кык вундӧгӧс ӧтластитігӧн ми корсям кык вундӧг костысь кратнӧй отношенньӧ либӧ прӧста отношенньӧ.

Ӧти вундӧглӧн мӧд дінӧ отношенньӧӧн шусьӧ отношенньӧыс сэтшӧм лыдлӧн, коді мурталӧ ӧти вундӧгӧс кутшӧмкӧ мера единицаясӧн, лыд дінӧ, коді мурталӧ мӧдсӧ сэтшӧм жӧ лыда единицаясӧн.

3. Кык вундӧглысь отношенньӧ корсигӧн вермас лоны кык случай.

I. Муртассяна вундӧгъяслӧн отношенньӧ — быдса либӧ дроба лыд. Тадз:

AB/CD = 5/3, либӧ AB : CD = 5 : 3.

Кык вундӧглӧн гижӧм отношенньӧ лыддьыссьӧ тадз. AB вундӧг CD вундӧг дінӧ относитчӧ сідз, кыдз 5 относитчӧ 3 дінӧ; либӧ: AB вундӧглӧн CD вундӧг дінӧ отношенньӧ 5/3 ыджда.

II. Муртасьтӧм вундӧгъяслӧн отношенньӧ — матыстӧм лыд. Сетӧма AB да CD вундӧгъяс (219 серп.). Ичӧтджык CD вундӧгсӧ босьтам мера единица пыдди. CD вундӧгсӧ пукталам AB вылӧ; медым сійӧ пуктыссяс AB вундӧг вылӧ 3 пӧв да нӧшта лоӧ CD-ысь ичӧтджык FB коляс. Гижам кӧ, мый AB/CD ≈ 3, AB да CD вундӧгъяс костын отношенньӧ лоӧ неточнӧй, а матыстӧм, да тырмытӧм: результатӧс гӧгрӧстӧм вылӧ ми эновтім FB коляс.

AB да CD вундӧгъяс костысь точнӧйджык отношенньӧ корсьӧм вылӧ CD вундӧгсӧ юкам ӧтыджда 10 юкӧнӧ да 0,1 CD босьтам выль мера единица пыдди. Медым тайӧ выль мера единица AB вундӧгӧ пуктыссьӧ 34 пӧв да нӧшта лоӧ 0,1 CD-ысь ичӧтджык KB коляс.

Гижам: 3,4 CD < AB < 3,5 CD, либӧ AB/CD ≈ 3,4 тырмытӧмӧн да AB/CD ≈ 3,5 лишкаӧн. 3,4 да 3,5 отношенньӧясӧс арталӧма босьтӧм мераысь 0,1-ӧдз точносьтӧн. Кыдз лыдъясӧс юкигӧн, сідз жӧ и вундӧгъяс костысь отношенньӧ арталігӧн отношенньӧсӧ босьтӧны нетырӧн (с недостатком) сэк, кор колясыс босьтӧм мера единица джынысь ичӧтджык, а кор колясыс босьтӧм мера единица джынысь ыджыдджык, сэк отношенньӧсӧ босьтӧны лишкаӧн (с избытком).

AB да CD вундӧгъяс костысь нӧшта точнӧйджык отношенньӧ корсьӧм вылӧ CD вундӧгсӧ юкам ӧтыджда 100 юкӧнӧ. Медым 0,01 CD пуктыссьӧ KB коляс вылӧ 3-ысь да бара лоӧ 0,01 CD дорысь ичӧтджык кутшӧмкӧ коляс.

Гижам: 3,43 CD < AB < 3,44 CD, либӧ AB/CD ≈ 3,43 нетырӧн, либӧ AB/CD ≈ 3,44 лишкаӧн.

3,43 да 3,44 лыдъяс AB да CD вундӧгъяс костын отношенньӧяс, кодъясӧс арталӧма 0,01 точносьтӧн, ӧтиыс — нетыра, а мӧдыс — лишкаа.

Бӧрйӧм мера единицаӧс кӧ юкны нӧшта посниджык десятичнӧй юкӧнъясӧ, пример вылӧ, 1000 либӧ 10000 да с. в. юкӧнӧ, лоӧ вундӧгъяслӧн помтӧм, непериодическӧй десятичнӧй дробӧн мыччӧдӧм отношенньӧ.

Тадзнас, муртассьытӧм кык вундӧглӧн отношенньӧыс лоӧ иррациональнӧй лыдӧн.

4. Кык вундӧг, кодъяслӧн эм ӧтувъя мера, коді на пиысь кыкнанас пуктыссьӧ быдса лыдысь, шусьӧны соизмеримӧй вундӧгъясӧн; вундӧгъяс, кодъяслӧн ӧтувъя мера абу, шусьӧны несоизмеримӧйясӧн. Несоизмеримӧй вундӧгъяслысь отношенньӧсӧ мыччӧдӧны матыстӧмӧн определённӧй точносьтӧдз.

Несоизмеримӧй вундӧгъяслӧн кык отношенньӧ лыддьыссьӧны ӧтыдждаӧн сэк, кор тайӧ отношенньӧяслӧн ӧтыдждаӧсь матыстӧм лыда значенньӧясыс, кодъясӧс арталӧма любӧй ӧткодь точносьтӧн да босьтӧма кыкнансӧ нетырӧн либӧ лишнӧйӧн. Пример вылӧ, кор

a/b ≈ 7,5 да c/d ≈ 7,5;

a/b ≈ 7,52 да c/d ≈ 7,52;

a/b ≈ 7,524 да c/d ≈ 7,524 да с. в.,

сэк a/b = c/d.

Сідзкӧ, кык вундӧглӧн отношенньӧ лоӧ рациональнӧй либӧ иррациональнӧй лыд, код вылӧ колӧ ӧктыны мӧд вундӧгсӧ, медым эськӧ лоис воддза вундӧгыс.

3 §. Пропорциональнӧй вундӧгъяс. Геометрическӧй пропорция.

Сетӧма нёль вундӧг: AB = a = 4 см, CD = b = 2 см, MN = c = 6 см да KL = d = 3 см (219 a серп.). Босьтам кӧ на пиысь кыклысь AB да CD-лысь отношенньӧ да мӧд кыклысь MN да KL-лысь отношенньӧ, лоӧ AB/CD = 4/2 = 2 да MN/KL = 6/3 = 2. Кыкнан отношенньӧыс 2 ыджда; сідзкӧ найӧ ӧтыдждаӧсь; та вӧсна AB/CD = MN/KL.

Равенство пасӧн ӧтлаалӧм кык ӧтыджда отношенньӧ шусьӧны геометрическӧй (кратнӧй) пропорцияӧн.

AB/CD = MN/KL равенство — геометрическӧй пропорция.

Бӧръя гижӧд лыддьыссьӧ тадз: AB вундӧг, либӧ прӧста AB, относитчӧ CD дінӧ, кыдз MN относитчӧ KL дінӧ, либӧ AB да CD вундӧгъяслӧн отношенньӧ сы ыджда жӧ, мый ыджда MN да KL вундӧгъяслӧн.

Геометрическӧй пропорция артмӧ нёль членысь. Геометрическӧй пропорцияӧс артмӧдӧны оз быдсяма нёль вундӧг; пример вылӧ, вундӧгъяс 4 см, 5 см, 8 см да 10 см геометрическӧй пропорция вӧчӧны; тадзсӧ сы вӧсна, мый 8/4 = 10/5; а вундӧгъяс: 4 см, 5 см, 6 см да 7 см геометрическӧй пропорция оз вӧчны: наысь он вермы вӧчны кык ӧтыджда отношенньӧ.

Вундӧгъясӧс мурталысь лыдъяс кӧ вӧчӧны геометрическӧй пропорция, татшӧм нёль вундӧг йылысь шуӧны, мый найӧ пропорциональнӧйӧсь.

Нёль вундӧг шусьӧны пропорциональнӧйӧн, кор найӧс мурталысь лыдъяс вӧчӧны геометрическӧй пропорция.

Тадз, кор 4 вундӧг: a, b, c да d пропорциональнӧйӧсь, сэк эм равенство:

a/b = c/d, либӧ a : b = c : d.

4 §. Геометрическӧй пропорциялӧн свойствояс. Пропорцияяслӧн сикасъяс.

1. Геометрическӧй пропорциялӧн основнӧй свойствоыс сэтшӧми, мый пропорцияын шӧрса членъяслӧн произведенньӧ равняйтчӧ дорса членъяс произведенньӧлы.

2. Геометрическӧй пропорцияын местаясӧн позьӧ вежны: 1) дорса членъясӧс, 2) шӧрса членъясӧс, 3) ӧттшӧтш дорса да шӧрса членъясӧс.

3. Геометрическӧй пропорцияын позьӧ шӧрса членъясӧс пуктыны дорса членъяс местаӧ да дорса членъясӧс шӧрса членъяс местаӧ.

4. Непрерывнӧй пропорция. Геометрическӧй пропорция, кодлӧн дорса членъясыс либӧ шӧрса членъясыс ӧтыдждаӧсь, шусьӧ непрерывнӧйӧн. Непрерывнӧй геометрическӧй пропорциялӧн ӧткодь членыс шусьӧ средньӧй геометрическӧйӧн, либӧ мӧд кык членъяслӧн средньӧй пропорциональнӧйӧн.

a : b = b : c, либӧ b : a = c : b — непрерывнӧй пропорцияяс.

Пропорциялӧн основнӧй свойство серти лоӧ: b² = ac, кытысь .

Кык лыдлӧн средньӧй геометрическӧйыс равняйтчӧ найӧ произведенньӧысь квадратнӧй кореньлы.

5. Производнӧй пропорцияяс. a/b = c/d пропорцияын кыкнан пай дінас кӧ содтыны (либӧ чинтыны) 1-ӧн, равенство оз торксьы.

либӧ

либӧ

(I) производнӧй пропорцияӧс кӧ членӧн-членӧн юкны (II) вылӧ, лоӧ нӧшта производнӧй пропорция:

Первой отношенньӧса членъяслӧн сумма относитчӧ найӧ разносьт дінӧ сідз, кыдз мӧд отношенньӧса членъяслӧн сумма найӧ разносьт дінӧ.

6. Равнӧй отношенньӧяс радлӧн свойство.

Теорема. Сетӧма кӧ ӧтыджда отношенньӧяслӧн рад, воддза членъяслӧн сумма относитчӧ бӧръя членъяс сумма дінӧ сідз, кыдз воддза (предыдущӧй) членъяс пиысь быд ӧти относитчӧ ас бӧръя (последующӧй) дінӧ.

Сетӧма:

Колӧ докажитны:

Докажитӧм. Мед a/b = k, сэк сідзжӧ c/d = k, m/n = k да p/q = k да a = bk, c = dk, m = nk, p = qk. Бӧръя равенствояслысь членӧн-членӧн содтам веськыдвыв да шуйгавыв пайяссӧ да веськыдвыв пайысь ӧтувъя k босьтанлыд петкӧдам скобкаяс сайӧ; лоӧ:

a + c + m + p = k(b + d + n + q),

кытысь

но

та вӧсна

5 §. Пельӧслысь бокъяссӧ вомӧналысь параллельнӧй веськыд визьяслӧн свойство.

BAC пельӧслысь бокъяссӧ вомӧналам параллельнӧй веськыдъясӧн: BC, DE, KL да с. в. (220 серп.); ӧти сійӧ жӧ параллельнӧйяс серти пельӧс бокъяс вылӧ ӧткодя пукталӧм вундӧгъяс шусьӧны соответственнӧя пукталӧм вундӧгъясӧн.

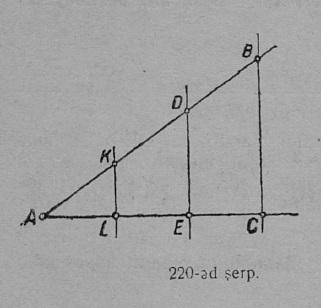
Вундӧгъяс AK да AL, KD да LE, AB да AC, KB да LC — соответственнӧя пукталӧм вундӧгъяс; вундӧгъяс AK да EC, либӧ KB да DB, либӧ KL да AL оз лоны соответственнӧя пукталӧмаясӧн.

Теорема. Пельӧслысь бокъяссӧ кӧ вомӧнавны кык параллельнӧй веськыдӧн, ӧти бок вывса любӧй кык вундӧглӧн отношенньӧ сы ыджда жӧ, мый ыджда мӧд бок вывса соответственнӧя пуктӧмаяслӧн; сідзкӧ, пельӧс бокъяс вылын артман нёль вундӧг — пропорциональнӧйӧсь.

Сетӧма: ∠BAC пельӧсын BC ∥ ED (221 серп.).

__________________________________

Колӧ докажитны:

1) AE/EC = AD/DB; 2) AC/EC = AB/DB; 3) AC/AE = AB/AD.

Докажитӧм. Медым кутшӧмкӧ q вундӧг лоӧ AC бок вывса AE да EC вундӧгъяслӧн ӧтувъя мера, сэк AE = mq, EC = nq да

AC = (m + n)q.

AC боксӧ юкан чутъяс пыр нуӧдам BC-лы, сідзкӧ и DE-лы, параллельнӧй веськыдъясӧс; AB боклӧн AD да DB вундӧгъяс юксясны сідзжӧ ӧтыджда юкӧнъясӧ: AD-ын сэтшӧм юкӧн лоӧ m, а DB-ын — n; на пиысь быд юкӧнлысь кузьта пасъям p пыр; сэк AD = mp, DB = np да AB = (m + n)p. Та ногӧн:

да

да

да

Теоремаыс лоӧ дзик веськыд тшӧтш и муртассьытӧм вундӧгъяслы.

Теорема (мӧдара). Пельӧслысь бокъяссӧ кык веськыд визьӧн вомӧналігӧн кӧ любӧй кык вундӧг ӧтар бок вывсьыс относитчӧны кыдзи кык соответственнӧй вундӧг мӧдар бок вылас, то сэтшӧм веськыдъясыс параллельнӧйӧсь.

Сетӧма:

BC да DE вомӧналӧны ∠BAC-лысь доръяс;

AE/EC = AD/DB (222 серп.).

__________________________________

Колӧ докажитны: BC ∥ DE.

Докажитӧм. Шуам, мый BC абу параллельнӧй DE-лы, а сылы параллельнӧй кутшӧмкӧ мӧд CF веськыд, коді мунӧ C пыр да AB бокӧс вомӧналӧ F чутын. Сэк веськыд теорема серти BAC пельӧс бокъяс вылын артмӧны пропорциональнӧй вундӧгъяс, мый вӧсна AE/EC = AD/DF. Артмӧм пропорцияӧс сетӧм AE/EC = AD/DB пропорциякӧд ӧтластитігӧн аддзам, мый, кор кык пропорцияын куим член ӧтыдждаӧсь, колӧ лоны ӧтыдждаӧн нёльӧд членъяслы: DF = DB. Тайӧ вермас лоны сӧмын сэк, кор F да B чутъяс ӧтлаасьӧны. Тайӧ петкӧдлӧ, мый миян шуӧм, мый BC абу параллельнӧй DE-лы, оз туй. Колӧ лоны BC ∥ DE.

Теорема. Параллельнӧй веськыдъяс кӧ вомӧналӧны пельӧслысь бокъяссӧ, то параллельнӧй визьяслӧн вундӧгъясыс относитчӧны, кыдзи найӧ соответственнӧй помъяслӧн пельӧс йывсянь расстоянньӧяс.

Сетӧма: ∠BAC; BC ∥ DE (223 серп.).

_____________________________

Колӧ докажитны:

BC/DE = AB/AD = AC/AE.

Докажитӧм. Нуӧдам отсасьысь веськыдӧс DF ∥ AC (223-ӧд серпас), сэк DE = FC. Видзӧдлам ∠ABC; сійӧс вомӧналӧны параллельнӧй AC да DF веськыдъяс, мый вӧсна BC/FC = BA/DA; FC-ӧс вежам сыкӧд ӧтыджда DE вундӧгӧн да лоӧ BC/DE = BA/DA, но AB/AD = AC/AE; та вӧсна BC/DE = AC/AE. Сідзкӧ,

BC/DE = AB/AD = AC/AE.

Теоремаыс лоӧ веськыд и сэтшӧм случайлы, кор вундӧгъясыс муртассьытӧмӧсь.

6 §. Пучоклысь лучьяссӧ вомӧналысь параллельнӧй веськыдъяслӧн свойствояс.

Теорема. Лучьяса пучок кӧ вомӧнавны параллельнӧй веськыд визьясӧн, то лучьяс вылас соответственнӧй вундӧгъяс да параллельнӧйяслӧн соответственнӧй вундӧгъяс пропорциональнӧйӧсь.

Сетӧма: O шӧрчута пучоклӧн лучьяс;

AM ∥ BN (224-ӧд серпас).

______________________________

Колӧ докажитны:

1) OA/AB = OC/CD = OE/EF = OM/MN;

2) BD/AC = DF/CE = FN/EM = ON/OM.

Докажитӧм. Быд кык луч вӧчӧны пельӧсъяс: BOD, DOF да FON; тайӧ пельӧсъясӧс вомӧналӧма кык параллельнӧй BN да AM веськыдъясӧн, кодъяс пельӧсъяс бокъяс вылын вундалӧны пропорциональнӧй вундӧгъясӧс; та вӧсна:

OA/AB = OC/CD; OC/CD = OE/EF; OE/EF = OM/MN.

Тайӧ пропорцияясӧс ӧтластитӧмысь петӧ, мый

OA/AB = OC/CD = OE/EF = OM/MN.

Теоремалысь лои докажитӧма первой юкӧнсӧ; мӧд юкӧн докажитӧм вылӧ вӧчам пропорцияяс, кодъясӧ пырасны BOD, DOF да FON пельӧсъяслысь доръяссӧ вундалысь параллельнӧй веськыдъяслӧн вундӧгъяс:

BD/AC = OB/OA = OD/OC;

DF/CE = OD/OC = OF/OE;

FN/EM = OF/OE = ON/OM.

Тайӧ пропорцияясӧс ӧтластитӧмысь петӧ, мый

BD/AC = DF/CE = FN/EM = ON/OM.

Теоремалысь лои докажитӧма мӧдӧд юкӧнсӧ.

7 §. Куимпельӧсаса пытшкӧс пельӧс биссектрисалӧн свойство.

Теорема. Куимпельӧсаын пытшкӧс пельӧс биссектриса юкӧ воча куйлысь боксӧ мӧд кык бокъяскӧд пропорциональнӧй юкӧнъясӧ.

Сетӧма: ∆ABC; BD — биссектриса;

∠α = ∠β (225-ӧд серп.).

____________________________

Колӧ докажитны: AD : DC = AB : BC.

Докажитӧм. C йыв пыр нуӧдам веськыдӧс CF ∥ BD AB бокӧс нюжӧдӧмкӧд F чутын вомӧнасьтӧдз.

Параллельнӧй BD да CF веськыдъяс вомӧналӧны A пельӧслысь бокъяссӧ да вундӧны найӧс пропорциональнӧй юкӧнъясӧ; та вӧсна AD : DC = AB : BF. BCF куимпельӧсаын ∠F = ∠α кыдз BD да FC параллельнӧйяс да AF вундысь бердын соответственнӧй пельӧсъяс да ∠β = ∠BCF сійӧ жӧ параллельнӧйяс да BC вундысь бердын пытшкӧс крестӧнкуйлысь пельӧсъяс. Но ∠α = ∠β; сідзкӧ, ∠F = ∠C; тайӧ пельӧсъяс BCF куимпельӧсаын CF подувтас бердса пельӧсъяс; найӧ ӧтыдждаӧсь, мый вӧсна ∆BCF — кык ӧткузя бока да BF = BC. Артмӧм пропорцияысь BF вундӧгӧс вежам сыкӧд ӧтыдждаӧн — BC вундӧгӧн, лоӧ: AD : DC = AB : BC.

8 §. Нёльӧд пропорциональнӧй вундӧгӧс вӧчӧм.

Задача. Сетӧма куим вундӧг: a, b да c (226-ӧд серпас). Вӧчны нёльӧд вундӧг, налы пропорциональнӧйӧс.

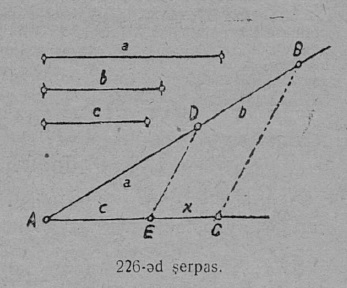
Построенньӧ. Колӧ вӧчны сэтшӧм вундӧг x, коді мед удовлетворяйтіс a : b = c : x пропорциялы.

Босьтам произвольнӧй ∠BAC; ӧти бок кузяыс A йывсянь водзысь-водзӧ пуктам вундӧгъяс: AD = a, DB = b, а мӧдыс кузя — вундӧг: AE = c; D да E чутъяссӧ ӧтлаалам DE веськыдӧн, нуӧдам BC ∥ DE, сэк EC = x лоӧ корсян нёльӧд пропорциональнӧй вундӧгӧн. Тадзсӧ сы вӧсна, мый BC ∥ ED, та вӧсна a : b = c : x.

9 §. Сетӧм отношенньӧын вундӧгӧс юкӧм.

Задача. AB = a вундӧгӧс юкны сэтшӧм кык вундӧгӧ: AC да CB, кодъяслӧн отношенньӧ мед вӧлі кык сетӧм m да n лыдъяслӧн отношенньӧ ыджда (227-ӧд серпас).

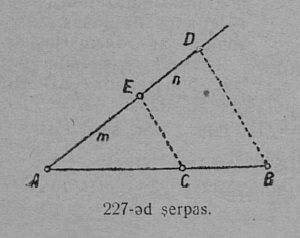
Построенньӧ. Задача условийӧ серти AC : CB = m : n.

Медым m = 4 да n = 3. Вӧчам произвольнӧй ∠BAD; ӧти бокыс кузя йывсяньыс пуктам AB = a вундӧг, а мӧдыс кузя водзысь-водзӧ вундӧгъяс: AE = m да ED = n. B да D чутъяс ӧтлаалам веськыд визьӧн, E юкан чут пыр нуӧдам веськыдӧс EC ∥ BD, коді AB-ӧс вундас C чутын. Тайӧ C чут AB вундӧгӧс юкас m : n отношенньӧын. Тайӧ сы вӧсна, мый EC ∥ BD, та вӧсна

AC/CB = AE/ED = m/n.

Юасянъяс да упражненньӧяс.

1. Пропорциональнӧйӧсь-ӧ вундӧгъяс, кор на пиысь кыклӧн отношенньӧ = 62,1 : 18, а мӧд кыклӧн = 41,1 : 12?

2. ABC куимпельӧсаын кутшӧмкӧ ӧти бок вылысь корсьны сэтшӧм M чут, медым сійӧн сійӧ юксис мукӧд кык боклы пропорциональнӧй юкӧнъясӧ.

3. Кык ӧткузя бока ABC куимпельӧсаын бокъяс относитчӧны кыдз 1 : 4; сылӧн периметр P = 4,5 см. Корсьны бокъяслысь кузьтасӧ.

4. Вӧчны став лоны вермана пропорцияяс произведенньӧяс равенствоясысь: 1) x∙y = m∙n; 2) 12∙8 = 16∙6.

5. Сетӧма a = 5 см да b = 8 см бокъяса веськыднёльпельӧса. Вӧчны сыкӧд ӧтгырся c = 6 см дора веськыднёльпельӧсаӧс. Сылысь мӧд боксӧ корсьны построенньӧӧн.

6. Сетӧма a = 16 см подувтаса куимпельӧса. Сылысь ӧтарбокса боксӧ юкӧма подувтассянь пондӧмӧн 3 юкӧнӧ 2 : 3 : 5 отношенньӧын. Юкан чутъяс пыр нуӧдӧма подувтаслы параллельнӧйясӧс. Артавны бокъяс костӧ йӧртӧм тайӧ параллельнӧй вундӧгъяслысь кузьтаяс.

XVI. ФИГУРАЯСЛӦН ПОДОБИЙӦ.

1 §. Подобнӧй унапельӧсаяс.

1. Участоклысь плансӧ чертитігӧн либӧ машина детальяс техническӧй чертёжъяс выполняйтігӧн вӧчӧны участоклысь либӧ машина детальяслысь ичӧтмӧдӧм контуръяс, фигуралысь формасӧ став подробносьтъяснас ньӧти вежлавтӧг кольӧмӧн.

Фигуралысь став линейнӧй размеръяссӧ ӧтмында пӧв ичӧтмӧдӧмӧн да пельӧсъясыслысь величинаяссӧ вежтӧг кольӧмӧн фигуралӧн форма оз вежсьы, артмӧ сылӧн ичӧтмӧдӧм изображенньӧ; изображенньӧыс фигурасьыс торъялӧ сӧмын ас размеръяснас.

2. 228 серпас вылын сетӧма ӧтмытта бока ABCDE да A₁B₁C₁D₁E₁ унапельӧсаяс; налӧн пельӧсъяс ӧтыдждаӧсь: ∠A = ∠A₁; ∠B = ∠B₁; ∠C = ∠C₁; ∠D = ∠D₁; ∠E = ∠E₁; таысь ӧтдор, соответственнӧй бокъяслӧн отношенньӧяс сідзжӧ ӧтыдждаӧсь:

A₁B₁/AB = B₁C₁/BC = C₁D₁/CD = D₁E₁/DE = E₁A₁/EA = k.

Татшӧм кык унапельӧса шусьӧны подобнӧйясӧн.

Кык унапельӧса шусьӧны подобнӧйясӧн, кор налӧн ӧтмында бок, соответственнӧй пельӧсъяс ӧтыдждаӧсь да сходственнӧй бокъясыс пропорциональнӧйӧсь.

Унапельӧсаяслӧн сходственнӧй бокъясӧн шусьӧны сэтшӧм бокъяс, кодъяс бердын куйлӧны соответственнӧй ӧтыджда пельӧсъяс. Подобийӧ пасйыссьӧ ∼ пасӧн.

Гижӧд A₁B₁C₁D₁E₁ ∼ ABCDE лыддьӧны тадз: A₁B₁C₁D₁E₁ унапельӧса подобнӧй ABCDE унапельӧсалы.

Кык подобнӧй унапельӧса сходственнӧй бокъяслӧн отношенньӧ шусьӧ подобийӧ коэффициентӧн.

Кор унапельӧсаяслӧн подобие коэффициентыс, либӧ мӧд ног кӧ, отношенньӧ A₁B₁/AB = k = 1, сэк унапельӧсаяс ӧтыдждаӧсь. Татысь петӧ, мый равенство лоӧ подобиелӧн частнӧй случай.

2 §. Куимпельӧсаяслӧн подобие.

Куимпельӧсаяс шусьӧны подобнӧйясӧн, кор налӧн соответственнӧя ӧтыдждаӧсь пельӧсъяс да сходственнӧй бокъяс пропорциональнӧйӧсь.

Куимпельӧсаясын сходственнӧй бокъяс куйлӧны ӧтыджда пельӧсъяс водзын.

Теорема. Куимпельӧсаын кутшӧмкӧ ӧти боклы параллельнӧй веськыд визь вундӧ куимпельӧсаысь сылы подобнӧй куимпельӧса.

Сетӧма:

ABC куимпельӧсаын вундӧг C₁A₁ ∥ CA

(229-ӧд серпас).

______________________________________

Колӧ докажитны: ∆A₁BC₁ ∼ ∆ABC, мӧд ногӧн:

1) ∠A = ∠A₁; ∠C = ∠C₁;

2) BA₁/BA = BC₁/BC = C₁A₁/CA.

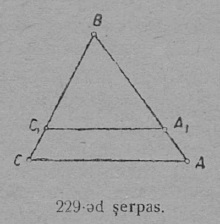
Докажитӧм. Нуӧдам C₁A₁ ∥ CA. Лоӧ ∆A₁BC₁. Сылӧн да ∆ABC-лӧн пельӧсъяс ӧтыдждаӧсь: ∠B — ӧтувъя, ∠A₁ = ∠A да ∠C₁ = ∠C кыдз соответственнӧйяс. Лучьяс пучок йылысь теорема серти лоӧ:

BA₁/BA = BC₁/BC = C₁A₁/CA;

сідзкӧ, куимпельӧсаяс подобнӧйӧсь,

∆A₁BC₁ ∼ ∆ABC.

3 §. Куимпельӧсаяс подобийӧ йылысь куим признак.

1. Куимпельӧсаяслӧн подобийӧ йылысь первой признак.

Теорема. Ӧти куимпельӧсалӧн кӧ кык пельӧс мӧд куимпельӧса кык пельӧскӧд соответственнӧя ӧтыдждаӧсь, куимпельӧсаяс подобнӧйӧсь.

Сетӧма: ABC куимпельӧсаын да A₁B₁C₁ куимпельӧсаын

∠A₁ = ∠A да ∠B₁ = ∠B (230 серп.).

_________________________

Колӧ докажитны: ∆A₁B₁C₁ ∼ ∆ABC.

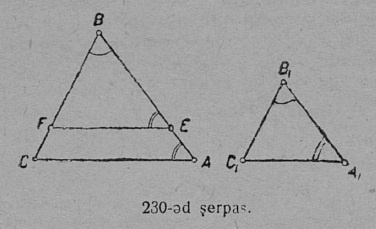
Докажитӧм. Условийӧ серти ∠A = ∠A₁ да ∠B = ∠B₁, сідзкӧ и ∠C = ∠C₁ кыдз 2d-ӧдз сетӧм пельӧсъяс суммалӧн содтӧд. B йывсянь BA бок кузя пуктам вундӧг BE = B₁A₁ да нуӧдам FE ∥ CA, лоӧ ∆EBF ∼ ∆ABC; сы вӧсна, мый BE = B₁A₁ да ∠B = ∠B₁ условийӧ серти да ∠E = ∠A = ∠A₁, ∆EBF = ∆A₁B₁C₁; но ∆EBF ∼ ∆ABC, сідзкӧ и сыкӧд ӧтыджда ∆A₁B₁C₁ ∼ ∆ABC.

Следствийӧяс. 1) Веськыдпельӧса куимпельӧсаяс подобнӧйӧсь, кор налӧн эмӧсь ӧти ӧтыджда ёсь пельӧсӧн.

2) Кык ӧткузя бока куимпельӧсаяс подобнӧйӧсь, кор налӧн йыв бердса пельӧсъяс либӧ подувтас бердса пельӧсъяс ӧтыдждаӧсь.

3) Ӧткузя бокъяса куимпельӧсаяс подобнӧйӧсь.

2. Куимпельӧсаяс подобийӧ йылысь мӧд признак.

Теорема. Ӧти куимпельӧсалӧн кӧ кык бокыс пропорциональнӧйӧсь мӧд куимпельӧса кык боклы да тайӧ бокъяс костса пельӧсъясыс ӧтыдждаӧсь, куимпельӧсаяс подобнӧйӧсь.

Сетӧма: ∆ABC да ∆A₁B₁C₁;

A₁B₁/AB = A₁C₁/AC; ∠A₁ = ∠A (231 серпас).

________________________________

Колӧ докажитны: ∆A₁B₁C₁ ∼ ∆ABC.

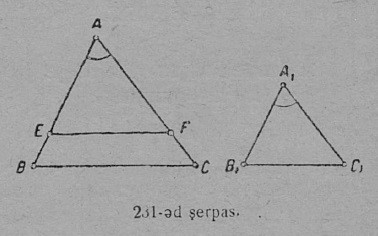
Докажитӧм. A йывсянь AB бок кузя пуктам вундӧг AE = A₁B₁ да нуӧдам EF ∥ BC, лоӧ ∆AEF ∼ ∆ABC. Куимпельӧсаяс подобийӧысь петӧ: AE/AB = AF/AC (1); (1) пропорцияын AE-ӧс A₁B₁-ӧн вежӧм бӧрын лоӧ: A₁B₁/AB = AF/AC (2).

(2) равенствоӧс условийӧын сетӧм пропорциякӧд ӧтластитігӧн аддзам, мый налӧн куим член ӧткодьӧсь; та вӧсна колӧ и нёльӧд членъяслы лоны ӧтыдждаӧн: AF = A₁C₁; сы вӧсна, мый ∠A₁ = ∠A условийӧ серти, AE = A₁B₁ построенньӧ серти да AF = A₁C₁ докажитӧм серти, ∆A₁B₁C₁ = ∆AEF. ∆AEF ∼ ∆ABC, сідзкӧ и сыкӧд ӧтыджда ∆A₁B₁C₁ ∼ ∆ABC.

Следствийӧ. Веськыдпельӧса куимпельӧсаяс подобнӧйӧсь, кор найӧ катетъяслӧн отношенньӧяс ӧтыдждаӧсь.

3. Куимпельӧсаяс подобийӧ йылысь коймӧд признак.

Теорема. Ӧти куимпельӧсалӧн кӧ куимнан бокыс пропорциональнӧйӧсь мӧд куимпельӧсаса куим боклы, куимпельӧсаяс подобнӧйӧсь.

Сетӧма: ∆ABC да ∆A₁B₁C₁;

A₁B₁/AB = B₁C₁/BC = C₁A₁/CA (232 серп.).

_______________________________

Колӧ докажитны: ∆A₁B₁C₁ ∼ ∆ABC.

Докажитӧм. A йывсянь AB бок кузя пуктам вундӧг AE = A₁B₁ да нуӧдам EF ∥ BC, сэк ∆AEF ∼ ∆ABC. Куимпельӧсаяс подобийӧысь петӧ, мый

AE/AB = AF/AC = EF/BC. (1)

Первой отношенньӧысь AE-ӧс вежам A₁B₁-ӧн да лоӧ:

A₁B₁/AB = AF/AC = EF/BC. (2)

(2) пропорцияӧс условийӧын сетӧм пропорциякӧд ӧтластитӧмысь петӧ, мый AF/AC = A₁C₁/AC, кытысь AF = A₁C₁ да EF/BC = B₁C₁/BC, кытысь EF = B₁C₁. Тадз, AEF куимпельӧсалӧн 3-нан бокыс A₁B₁C₁ куимпельӧсаса куимнан бок ыджда; та вӧсна, ∆AEF = ∆A₁B₁C₁, но ∆AEF ∼ ∆ABC, сідзкӧ сыкӧд ӧтыджда ∆A₁B₁C₁ ∼ ∆ABC.

Следствийӧ. Кык ӧткузя бока куимпельӧсаяс подобнӧйӧсь, кор ӧтиыслӧн подувтас да боквывса бокыс пропорциональнӧйӧсь мӧд куимпельӧсаса подувтаслы да боквывса боклы.

4. Теорема. Кык веськыдпельӧса куимпельӧса подобнӧйӧсь, кор ӧтиыслӧн гипотенуза да катет пропорциональнӧйӧсь мӧд куимпельӧсаса гипотенузалы да катетлы.

Сетӧма: ∆ABC да ∆A₁B₁C₁; A₁B₁/AB = B₁C₁/BC (233 серп.).

___________________________

Колӧ докажитны: ∆A₁B₁C₁ ∼ ∆ABC.

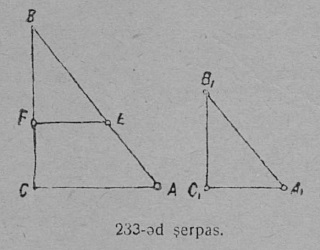
Докажитӧм. B йывсянь BA гипотенуза кузя пуктам вундӧг BE = B₁A₁ да нуӧдам EF ∥ AC. ∆BEF ∼ ∆ABC, мый вӧсна BE/BA = BF/BC; артмӧм пропорцияӧс сетӧмкӧд ӧтластитӧмысь петӧ, мый BF = B₁C₁; сідзкӧ, ∆EBF = ∆A₁B₁C₁ гипотенуза да катет серти. Но ∆EBF ∼ ∆ABC, сідзкӧ и сыкӧд ӧтыджда ∆A₁B₁C₁ ∼ ∆ABC.

4 §. Подобнӧй куимпельӧсаясса судтаяслӧн да доръяслӧн пропорциональносьт.

1. Теорема. Подобнӧй куимпельӧсаяслӧн судтаяс пропорциональнӧйӧсь сходственнӧй бокъяслы.

Сетӧма:

∆ABC ∼ ∆A₁B₁C₁; BD да B₁D₁ — судтаяс (234-ӧд серп.).

_____________________________________________

Колӧ докажитны:

B₁D₁/BD = A₁B₁/AB = B₁C₁/BC = C₁A₁/CA.

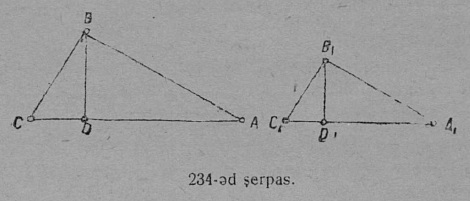
Докажитӧм. ABD да A₁B₁D₁ веськыдпельӧса куимпельӧсаяс подобнӧйӧсь сы вӧсна, мый налӧн кыкнаныслӧн эмӧсь ӧтыджда ёсь пельӧсӧн ∠A = ∠A₁. Подобийӧысь петӧ: B₁D₁/BD = A₁B₁/AB, но A₁B₁/AB = B₁C₁/BC = C₁A₁/CA, та вӧсна

B₁D₁/BD = A₁B₁/AB = B₁C₁/BC = C₁A₁/CA, м. л.,

подобнӧй куимпельӧсаяслӧн судтаяс пропорциональнӧйӧсь сходственнӧй бокъясысь любӧй гозлы.

2. Подобнӧй куимпельӧсаясын сходственнӧй биссектрисаяс да медианаяс пропорциональнӧйӧсь сходственнӧй бокъяслы.

3. Кор геометрическӧй задачаӧс решитігӧн пӧльзуйтчам куимпельӧсаяс подобийӧӧн, бурджык вӧчны пропорциясӧ сідз, медым ӧти отношенньӧын членъясӧн вӧліны линейнӧй элементъяс ӧти куимпельӧсаысь, а мӧдын — сходственнӧй элементъяс мӧд куимпельӧсаысь.

5 §. Подобнӧй куимпельӧсаяслӧн свойствояс вылын подувтасассян приборъяс.

1. Юкысь циркуль. Юкысь циркульӧн пӧльзуйтчӧны чертёжнӧй уджъяс вӧчигӧн (235-ӧд серп.). Сійӧн юклӧны вундӧгъясӧс ӧтыджда юкӧнъясӧ. Сійӧс вӧчӧма куимпельӧсаяс подобийӧ подувтас вылын. Юкысь циркульӧс вӧчӧма кык ёсь помъяса AD да CB планкаясысь; планкаяс кузяыс вӧчӧма коласъяс (прорезъяс); планкаясыс мӧда-мӧдыскӧд ӧтлаасьӧны подвижнӧй O шарнирӧн. Шуам, медым колӧ PQ вундӧгӧс юкны куим ӧтыджда юкӧнӧ. Та могысь O шарнирсӧ колӧ сідзи крепитны, медым BO лои 3 пӧв ыджыдджык OC серти; арталӧмъяс кокньӧдӧм могысь AD да CB кокъяс вылын эм деленньӧяс. O шарнирсӧ крепитӧм бӧрын планкаяслысь B да D помъяссӧ пуктӧны вундӧгса P да Q чутъясӧ; сэк C да A костса расстоянньӧ лоӧ ⅓PQ ыджда. Тайӧ сы вӧсна, мый ∆COA ∼ ∆BOD, кытысь CA/BD = OC/OB, но CO = ⅓OB; сідзкӧ, CA/BD = 1/3; та вӧсна CA = ⅓BD, либӧ CA = ⅓PQ, сы вӧсна, мый BD = PQ.

2. Вомӧна масштаб. Визя масштабӧн он вермы точнӧя пуктавны масштаб единицалысь посни юкӧнъяссӧ; тайӧ неудобствоысь позьӧ мынтӧдчыны вомӧна масштабӧн, код отсӧгӧн позьӧ пуктавны масштабнӧй единицалысь дасӧд да сёӧд юкӧнъяс. Кыдз вӧчсьӧ вомӧна масштаб, тыдалӧ 236-ӧд серпас вылысь.

Сыын масштаб единицаӧн лоӧ BA; CA = 0,1BA. AOC куимпельӧсаысь, код пытшкӧсті нуӧдӧма AC-лы веськыд параллельнӧйясӧс, петӧ, мый KL = 0,1CA, либӧ KL = 0,01BA; AOC куимпельӧсаын мукӧд параллельнӧйяс соответственнӧя ӧтыдждаӧсь BA мера единицаса 0,02; 0,03, ... 0,10-кӧд.

Кыдзи пользуйтчӧны вомӧна масштабӧн. Шуам, колӧ пуктыны вундӧг x = 2,35 AB. Циркульлысь ӧти ёсь помсӧ пуктам M чутӧ, а мӧдсӧ — N чутӧ; сэк NM = x = 2,35.

Збыльысь ӧд, MN = DM + ED + NE, кӧн DM = 2BA, NE = 0,3BA, ED = 0,05BA, тадзсӧ сы вӧсна, мый ∆OAC ∼ ∆ODE, кытысь OD/OA = ED/CA = 5/10; сідзкӧ, ED = CA∙5/10, но CA = 0,1BA; та вӧсна ED = 0,05BA.

Тадз, NM = 2 + 0,3 + 0,05 = 2,35.

6 §. Веськыдвизя подобнӧй фигураясӧс вӧчӧм.

Задача 1. Сетӧма ABC куимпельӧса. Колӧ вӧчны сылы подобнӧй куимпельӧса сідз, медым сылӧн доръясыс вӧліны сетӧма куимпельӧсаса бокъясысь куим пӧв ичӧтджыкӧсь (237-ӧд серп.).

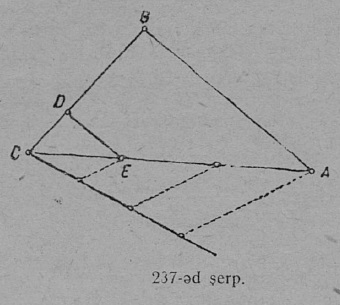
Построенньӧ. ABC куимпельӧсалысь кутшӧмкӧ ӧти боксӧ, шуам, AC, юкам куим ӧтыджда юкӧнӧ да E юкан чут пыр нуӧдам ED веськыдӧс ABC куимпельӧсаса AB боклы параллельнӧя; артман ∆EDC сетӧмкӧд подобнӧй.

∆EDC ∼ ∆ABC кыдз ӧтыджда пельӧсаяс.

Задача 2. Сетӧма ABC куимпельӧса да a вундӧг, a вундӧг вылӧ колӧ вӧчны куимпельӧса, медым сійӧ вӧлі сетӧмлы подобнӧй (238-ӧд серп.).

Построенньӧ. a вундӧгыс ABC куимпельӧсаса CA боккӧд сходственнӧй вундӧг. MN веськыд визь вылӧ пуктам C₁A₁ = a вундӧг да A₁ чут бердӧ вӧчам ∠A₁ = ∠A да C₁ чут бердӧ ∠C₁ = ∠C; артмас ∆A₁B₁C₁ ∼ ∆ABC. Тайӧ сы вӧсна, мый куимпельӧсаяслӧн эмӧсь кык ӧтыджда соответственнӧй пельӧсъясӧн.

Задача 3. Сетӧм ABC куимпельӧсаӧ впишитны квадрат сідз, медым сылӧн кык йыв куйлісны куимпельӧсаса подувтас вылын, а мӧд кык йыв — боквывса бокъяс вылын (239 с.).

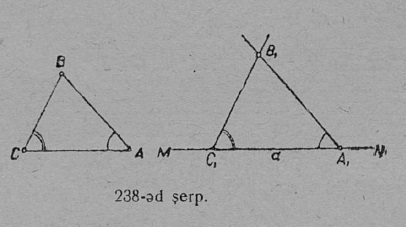
Решитӧм. Куимпельӧсаса AB боквывса произвольнӧй N чутысь нуӧдам AC боклы перпендикуляр NK да вӧчам KLMN квадрат, кодлӧн бокыс NK ыджда. Куимпельӧсаса A йылысь квадратса M йыв пыр BC боккӧд M₁ чутын вомӧнасьтӧдз нуӧдам AM₁ веськыдӧс; сэсся нуӧдалам M₁L₁ ⊥ AC, M₁N₁ ∥ AC да N₁K₁ ⊥ AC; лоӧ корсян квадрат — K₁N₁M₁L₁.

Докажитӧм. K₁L₁M₁N₁ — веськыднёльпельӧса. AL₁M₁ да ALM куимпельӧсаяс подобийӧысь лоӧ: M₁L₁/ML = M₁A/MA; AM₁N₁ да AMN куимпельӧсаяс подобиеысь лоӧ: M₁N₁/MN = M₁A/MA, сідзкӧ, M₁L₁/ML = M₁N₁/MN; ML = MN кыдз квадратлӧн бокъясыс построенньӧ серти, та вӧсна M₁L₁ = M₁N₁; лоӧ, мый K₁L₁M₁N₁ веськыднёльпельӧсаыс — квадрат.

7 §. Подобнӧя пукталӧм унапельӧсаяс. Подобийӧлӧн шӧрчут.

Задача. Вӧчны сетӧм унапельӧсалы подобнӧй унапельӧсаӧс.

Построенньӧ. ABCDE унапельӧса пытшкын кӧнкӧ босьтам S чут да сысянь йывъяс пырысь нуӧдалам лучьяс (240 серп.). Кутшӧмкӧ ӧти луч вылын, шуам SA вылын, босьтам A₁ чут (тайӧ чут позьӧ босьтны унапельӧса ортсын дай сы бок вылын) да нуӧдам веськыдӧс A₁B₁ ∥ AB SB лучкӧд B₁ чутын вомӧнасьтӧдз; B₁ чут пыр нуӧдам B₁C₁ ∥ BC SC лучкӧд C₁ чутын вомӧнасьтӧдз; сэсся C₁D₁ ∥ CD, D₁E₁ ∥ DE да ӧтлаалам E₁ A₁-кӧд; артмас A₁B₁C₁D₁E₁ унапельӧса, коді сетӧм ABCDE унапельӧсакӧд лоӧ подобнӧй.

Тайӧ тадз сы вӧсна, мый лучьяс пучок йылысь теорема серти лоӧ:

SA₁/SA = SB₁/SB = SC₁/SC = SD₁/SD = SE₁/SE.

Сы вӧсна, мый SA₁/SA = SE₁/SE, E₁A₁ ∥ EA.

A₁B₁ ∥ AB, B₁C₁ ∥ BC да с. в.; сідзкӧ, ∠A₁ = ∠A, ∠B₁ = ∠B, ∠C₁ = ∠C да с. в. кыдз параллельнӧй бокъяса пельӧсъяс, да

SA₁/SA = A₁B₁/AB = SB₁/SB = B₁C₁/BC = SC₁/SC =

= C₁D₁/CD = SD₁/SD = D₁E₁/DE = SE₁/SE = E₁A₁/EA.

Тайӧ отношенньӧяс равенствоысь петӧ, мый

A₁B₁/AB = B₁C₁/BC = C₁D₁/CD = D₁E₁/DE = A₁E₁/AE.

A₁B₁C₁D₁E₁ да ABCDE унапельӧсаяслӧн соответственнӧй пельӧсъяс ӧтыдждаӧсь да сходственнӧй бокъясыс пропорциональнӧйӧсь; сідзкӧ A₁B₁C₁D₁E₁ ∼ ABCDE. S чут шусьӧ подобийӧ шӧрчутӧн, а асьныс унапельӧсаясыс — подобнӧя пукталӧмъясӧн.

Ӧти унапельӧсаӧс кӧ мӧд серти вӧрзьӧдам, шуам, бергӧдам сійӧс, подобийӧ оз торксьы, а подобнӧя пукталӧмыс торксяс: сходственнӧй бокъяс оз лоны параллельнӧйӧсь да ӧтыджда пельӧсъяслысь йывъяс ӧтлаалысь лучьяс оз кутны мунны ӧти сійӧ жӧ чут пыр; унапельӧса воштас подобийӧлысь шӧрчутсӧ.

Медым унапельӧсаяс вӧліны подобнӧйӧсь, колӧ, медым налӧн: 1) соответственнӧй пельӧсъяс вӧліны ӧтыдждаӧсь да 2) сходственнӧй бокъяс вӧліны пропорциональнӧйӧсь. Подобнӧя пукталӧма унапельӧсаяслӧн, таысь ӧтдор, мед нӧшта вӧлі подобийӧлӧн шӧрчут.

8 §. Подобнӧй унапельӧсаяслӧн свойство.

Разнӧй масштабъясӧн планъяс вӧчалігӧн (перечерчивайтігӧн) бурджык овлӧ сетӧм плансӧ торйӧдавны торъя участокъясӧ да сэсся вӧчавны найӧс ӧтисӧ мӧдыс бӧрын. Унджыкысь плансӧ торйӧдавлӧны куимпельӧсаясӧ. Тадзик вӧчӧмсӧ (перечерчиванньӧ) подулалӧма со кутшӧм кык теорема вылын.

1. Теорема. Подобнӧй да подобнӧя пукталӧм унапельӧсаясса соответственнӧй ӧтыджда пельӧсъяс йывъяс пыр нуӧдӧм диагональяс торйӧдӧны найӧс ӧтмында подобнӧй да подобнӧя пукталӧм куимпельӧсаясӧ.

Сетӧма: A₁B₁C₁D₁E₁ ∼ ABCDE (241 серп.), м. л.

1) ∠A₁ = ∠A, ∠B₁ = ∠B да с. в.

2) A₁B₁/AB = B₁C₁/BC = C₁D₁/CD да с. в.

3) A₁D₁ да AD, A₁C₁ да AC — сходственнӧй диагональяс.

________________________________

Колӧ докажитны: 1) ∆A₁B₁C₁ ∼ ∆ABC;

2) ∆A₁C₁D₁ ∼ ∆ACD;

3) ∆A₁D₁E₁ ∼ ∆ADE.

Докажитӧм. Сы вӧсна, мый условие серти ∠B₁ = ∠B да A₁B₁/AB = B₁C₁/BC, ∆A₁B₁C₁ ∼ ∆ABC; найӧ подобийӧысь петӧ, мый ∠A₁C₁B₁ = ∠ACB; но ∠C₁ = ∠C, та вӧсна ∠A₁C₁D₁ = ∠ACD, таысь ӧтдор, B₁C₁/BC = A₁C₁/AC; а сы вӧсна, мый B₁C₁/BC = C₁D₁/CD, A₁C₁/AC = C₁D₁/CD. ∠A₁C₁D₁ = ∠ACD да A₁C₁/AC = C₁D₁/CD, та вӧсна ∆A₁C₁D₁ ∼ ∆ACD.

Тадз жӧ докажитӧны, мый ∆A₁D₁E₁ ∼ ∆ADE.

Следствие. Подобнӧй унапельӧсаяслӧн сходственнӧй диагональяс пропорциональнӧйӧсь сходственнӧй бокъяслы:

A₁B₁/AB = B₁C₁/BC = A₁C₁/AC = C₁D₁/CD = A₁D₁/AD да с. в.

2. Теорема (мӧдара). Кык унапельӧса кӧ сходственнӧй диагональясӧн торйӧдчӧны ӧтмында подобнӧй да подобнӧя пукталӧма куимпельӧсаясӧ, татшӧм унапельӧсаяс подобнӧйӧсь.

Сетӧма: ∆A₁B₁C₁ ∼ ∆ABC

∆A₁C₁D₁ ∼ ∆ACD

∆A₁D₁E₁ ∼ ∆ADE

да подобнӧя пукталӧмаӧсь (241-ӧд серпас).

______________________________

Колӧ докажитны: A₁B₁C₁D₁E₁ ∼ ABCDE, м. л.

1) ∠A = ∠A₁; ∠B = ∠B₁ да с. в.

2) A₁B₁/AB = B₁C₁/BC = C₁D₁/CD да с. в.

Докажитӧм. A₁B₁C₁ да ABC куимпельӧсаяс подобийӧысь петӧ, мый ∠B₁ = ∠B да ∠A₁C₁B₁ = ∠ACB (1). A₁C₁D₁ да ACD куимпельӧсаяс подобийӧысь петӧ, мый ∠A₁C₁D₁ = ∠ACD (2); (1) да (2) равенствоясӧс членӧн-членӧн содтӧмысь лоӧ ∠C₁ = ∠C; тадз жӧ докажитӧны унапельӧсаясса мукӧд пельӧсъяслысь равенство.

A₁B₁C₁ да ABC куимпельӧсаяс подобийӧысь петӧ: A₁B₁/AB = B₁C₁/BC = A₁C₁/AC; A₁C₁D₁ да ACD куимпельӧсаяс подобийӧысь: A₁C₁/AC = C₁D₁/CD; бӧръя кык равенствоӧс ӧтластитӧмысь артмас: A₁B₁/AB = B₁C₁/BC = C₁D₁/CD. Тадз жӧ докажитӧны унапельӧсаясса мукӧд бокъяслысь пропорциональносьт.

Та ногӧн, A₁B₁C₁D₁E₁ ∼ ABCDE.

9 §. Подобнӧй фигураяслӧн периметръяс костын отношенньӧ.

Теорема. Подобнӧй унапельӧсаяслӧн периметръяс относитчӧны кыдз унапельӧсаяслӧн сходственнӧй бокъяс.

Сетӧма: A₁B₁C₁D₁E₁ ∼ ABCDE (241-ӧд серпас).

_____________________________

Колӧ докажитны:

Докажитӧм. ABCDE да A₁B₁C₁D₁E₁ унапельӧсаяс подобийӧысь петӧ:

A₁B₁/AB = B₁C₁/BC = C₁D₁/CD = D₁E₁/DE = E₁A₁/ EA = k.

Ӧтыджда отношенньӧяс рад свойство серти лоӧ:

либӧ P₁/P = A₁B₁/AB, кӧн P₁ да P — сетӧм унапельӧсаяслӧн периметръяс.

Теорема справедливӧй любӧй лыда n бокъяса подобнӧй унапельӧсаяс йылысь; теорема справедливӧй сэтшӧм случай дырйи, кор n = 3, — подобнӧй куимпельӧсаяс йылысь.

10 §. Подобнӧй куимпельӧсаяслӧн да унапельӧсаяслӧн площадьяс костын отношенньӧ.

1. Кык куимпельӧсалӧн, кодъясын эм ӧти ӧтыджда пельӧсӧн, площадьясныс относитчӧны, кыдз тайӧ пельӧсъясӧс йӧртысь бокъяслӧн произведенньӧяс.

Сетӧма: ∆ABC да ∆A₁B₁C₁; ∠A = ∠A₁ (242-ӧд серп.)

_____________________________________

Колӧ докажитны:

Докажитӧм. Сетӧм куимпельӧсаясын нуӧдам CD да C₁D₁ судтаяс; лоӧ:

Сы вӧсна, мый ∆ACD да ∆A₁C₁D₁ веськыдпельӧсаӧсь да налӧн эм ӧтыджда ёсь пельӧсӧн: ∠A = ∠A₁, найӧ подобнӧйӧсь, кытысь петӧ, мый

CD/C₁D₁ = AC/A₁C₁. (2)

(1) равенствоысь CD/C₁D₁ отношенньӧсӧ вежам сыкӧд ӧтыджда AC/A₁C₁ отношенньӧӧн да лоӧ:

либӧ

Бӧръя гижӧдногнас сэк пӧльзуйтчӧны, кор бокъяссӧ петкӧдлӧма лыдъяс пыр.

Теорема лоӧ справедливӧй тшӧтш сэтшӧм случай дырйи, кор ∠A + ∠A₁ = 2d.

2. Теорема. Подобнӧй куимпельӧсаяслӧн площадьяс относитчӧны, кыдз сходственнӧй бокъяслӧн квадратъяс.

Сетӧма: ∆ABC ∼ ∆A₁B₁C₁ (243-ӧд серп.).

_________________________

Колӧ докажитны:

S/S₁ = AB²/A₁B₁² = AC²/A₁C₁² = BC²/B₁C₁².

Докажитӧм. ∆ABC ∼ ∆A₁B₁C₁, сідзкӧ, ∠A = ∠A₁, ∠B = ∠B₁, та вӧсна

Куимпельӧсаяс подобийӧысь петӧ, мый

AB/A₁B₁ = AC/A₁C₁ = BC/B₁C₁ (2)

(1) равенствоысь кутшӧмкӧ ӧти отношенньӧ вежам (2) равенствоса любӧй отношенньӧӧн; сэк лоӧ:

но

(AB/A₁B₁)² = (AC/A₁C₁)² = (BC/B₁C₁)²,

та вӧсна

S/S₁ = AB²/A₁B₁² = AC²/A₁C₁² = BC²/B₁C₁².

3. Теорема. Подобнӧй унапельӧсаяслӧн площадьяс относитчӧны кыдз сходственнӧй бокъяслӧн квадратъясыс.

Сетӧма: ABCDE ∼ A₁B₁C₁D₁E₁ (243 a-ӧд серп.).

_______________________________

Колӧ докажитны: S/S₁ = AB²/A₁B₁² = BC²/B₁C₁² = ...

Докажитӧм. Соответственнӧй A да A₁ йывъясысь нуӧдӧм диагональясӧн сетӧм унапельӧсаяс торйӧдчӧны ӧтмында соответственнӧя подобнӧй куимпельӧсаясӧ: ABC да A₁B₁C₁, ACD да A₁C₁D₁, ADE да A₁D₁E₁. Куимпельӧсаяс подобийӧысь петӧ:

ABC пл./A₁B₁C₁ пл. = AB²/A₁B₁² = BC²/B₁C₁²;

ACD пл./ A₁C₁D₁ пл. = CD²/C₁D₁²;

AED пл./A₁E₁D₁ пл. = ED²/E₁D₁² = AE²/A₁E₁². (1)

Унапельӧсаяс подобийӧысь петӧ:

AB/A₁B₁ = BC/B₁C₁ = CD/C₁D₁ = DE/D₁E₁ = EA/E₁A₁,

либӧ

AB²/A₁B₁² = BC²/ B₁C₁² = CD²/C₁D₁² =

=DE²/D₁E₁² = EA²/E₁A₁². (2)

(1) да (2) радса отношенньӧясӧс ӧтластитӧмысь лоӧ:

ABC пл./A₁B₁C₁ пл. = ACD пл./ A₁C₁D₁ пл. =

=AED пл./A₁E₁D₁ пл. = AB²/A₁B₁² = ...

Ӧтыджда отношенньӧяс рад свойство серти лоӧ:

= ABCDE пл./A₁B₁C₁D₁E₁ пл. =

=AB²/A₁B₁² =BC²/B₁C₁² = ...

Юасянъяс да упражненньӧяс.

1. Мый вӧсна соответственнӧя параллельнӧй да перпендикулярнӧй бокъяса куимпельӧсаяс подобнӧйӧсь?

2. Мый вӧсна квадрат да веськыднёльпельӧса абу подобнӧйӧсь, кӧть налӧн пельӧсъясыс, кыдз веськыдъяс, ӧтыдждаӧсь?

3. Мый вӧсна a бока квадрат да 2a бока ромб абу подобнӧйӧсь, кӧть налӧн бокъясыс пропорциональнӧйӧсь?

4. Медым куимпельӧсаяс вӧліны подобнӧйӧсь, сӧмын колӧ, мед налӧн пельӧсъясыс вӧліны ӧтыдждаӧсь либӧ бокъясыс пропорциональнӧйӧсь. Тырмӧ-ӧ кодыскӧ тайӧ ӧти условийӧыс сы вылӧ, медым ӧтмында бока кык унапельӧса вӧліны подобнӧйӧсь?

5. Вӧчны произвольнӧй формаа ABC куимпельӧсаӧс да лучьяс пучок способӧн вӧчны сылы подобнӧйӧс; подобийӧлӧн коэффициент k = 1,5.

6. ABC куимпельӧсаын бокъяс AB = 6 см, BC = 8 см да AC = 9 см. Артавны подобнӧй куимпельӧсалысь бокъяс, кор k = 2,5.

7. Трапециялӧн диагональяс мӧда-мӧдӧн юксьӧны торъясӧ, кодъяс пропорциональнӧйӧсь подувтасъяслы. Докажитны.

8. ABC куимпельӧсаын A да C пельӧсъяс йывъясысь нуӧдӧма AA₁ да CC₁ медианаяс (244-ӧд серпас). Докажитны, мый C₁A₁ веськыд сетӧм куимпельӧсаысь вундӧ сылы подобнӧй куимпельӧсаӧс да AA₁ да CC₁ мӧда-мӧдӧн юксьӧны 2 : 1 отношенньӧын.

9. Сетӧма куим куимпельӧса, кодъяслӧн бокъяс: 1) 10; 8 да 12; 2) 7,5; 6 да 7,2; 3) 25; 20 да 24. Определитны, кутшӧм куимпельӧсаяс на пиын подобнӧйӧсь.

10. a = 10 см подувтаса да h = 15 см судтаа куимпельӧсаӧ впишитӧма квадрат, кодлӧн кык йыв куйлӧны куимпельӧсаса подувтас вылын, а мӧд кык йыв — боквывса бокъяс вылас. Тӧдмавны квадрат боклысь кузьта.

11. Пельӧсӧ впишитӧма ортсысянь касайтчысь кык кытшвизь, кодъяслӧн шӧрчутъясыс пельӧс йывсянь 9 см да 3 см ылнаынӧсь. Тӧдмавны тайӧ кытшвизьяс радиусъяслысь кузьтаяссӧ.

12. ABCD веськыднёльпельӧса пытшкӧ пуктӧма мӧд A₁B₁C₁D₁ веськыднёльпельӧса, кодлӧн бокъясыс параллельнӧйӧсь сетӧм веськыднёльпельӧса бокъяслы да насянь ӧтылнаынӧсь. Подобнӧйӧсь-ӧ тайӧ веськыднёльпельӧсаясыс?

XVII. КУИМПЕЛЬӦСАЛӦН ЭЛЕМЕНТЪЯС КОСТЫН МЕТРИЧЕСКӦЙ СООТНОШЕННЬӦЯС.

1 §. Куимпельӧсалӧн элементъяс костын зависимосьт.

1. Любӧй куимпельӧсаын пельӧсъяс костын зависимосьт определяйтчӧ равенствоӧн:

∠A + ∠B + ∠C = 2d.

2. Куимпельӧса бокъяс костын эм со кутшӧм зависимосьт: куимпельӧсалӧн любӧй бок мӧд кык бок суммаысь ичӧтджык, а найӧ разносьтысь ыджыдджык:

a < b + c да a > b − c, либӧ b − c < a < b + c.

3. Куимпельӧсаын бокъяс да пельӧсъяс костын эм татшӧм зависимосьт:

а) ыджыдджык бок водзын куйлӧ ыджыдджык пельӧс да, мӧдарӧ, ыджыдджык пельӧс водзын куйлӧ ыджыдджык бок: кор AC > BC, сэк ∠B > ∠A; кор ∠B > ∠A, сэк AC > BC.

Тайӧ теоремаяс оз устанавливайтны определённӧй лыда зависимосьтъяс куимпельӧсаса бокъяс костысь да накӧд йитчана элементъяс костысь — судта, бокъяслӧн проекция, медиана да с. в. — да сідзжӧ бокъяс да пельӧсъяс костысь.

Водзынджык вайӧдӧм теоремаяс тыртӧны тайӧ пробел да урчитӧны лыда зависимосьтсӧ куимпельӧса линейнӧй элементъяс костын; куимпельӧсаса бокъяс да пельӧсъяс костса лыда зависимосьтсӧ велӧдӧ математикалӧн особӧй юкӧн — тригонометрия.

2 §. Веськыдпельӧса куимпельӧсаын элементъяс костын метрическӧй соотношенньӧяс.

1. Теорема. Судта, кодӧс нуӧдӧма куимпельӧсаын веськыд пельӧс йывсянь гипотенуза вылӧ, юкӧ куимпельӧсасӧ кык подобнӧй куимпельӧсаӧ, кодъяс лоӧны подобнӧйӧсь сетӧм куимпельӧсаыскӧд.

Сетӧма:

ABC куимпельӧсаын ∠ACB = d; CD ⊥ AB

(245-ӧд серпас).

__________________________________

Колӧ докажитны: ∆ADC ∼ ∆BDC ∼ ∆ABC.

Докажитӧм. Видлалам веськыдпельӧса куимпельӧсаяс:

1) ∆ACD да ∆ABC. Налӧн ∠1 — ӧтувъя, сідзкӧ найӧ ӧтыдждапельӧсаӧсь, та вӧсна подобнӧйӧсь. ∆ACD ∼ ∆ABC.

2) ∆BCD да ∆ABC. Налӧн ∠4 — ӧтувъя, сідзкӧ, найӧ ӧтыдждапельӧсаӧсь, та вӧсна подобнӧйӧсь. ∆BCD ∼ ∆ABC.

3) ∆ACD да ∆CBD. Тайӧ куимпельӧсаяс кыкнаныс подобнӧйӧсь сетӧм ABC куимпельӧсалы, сідзкӧ асьныс найӧ мӧда-мӧдыскӧд подобнӧйӧсь.

∆ACD ∼ ∆ABC да ∆CBD ∼ ∆ABC;

сідзкӧ, ∆ACD ∼ ∆CBD.

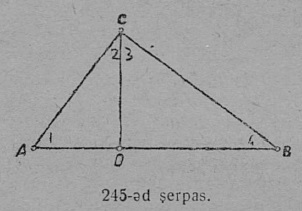
2. Теорема. Веськыд пельӧс йывсянь гипотенуза дорӧ нуӧдӧм судта эм катетъяслӧн гипотенуза вылӧ проекцияяс костын средньӧй пропорциональнӧй.

Сетӧма:

ABC куимпельӧсаын ∠ACB = d, CD ⊥ AB

(245-ӧд серпас).

______________________________

Колӧ докажитны: AD : CD = CD : DB.

Докажитӧм. ∆ACD да ∆CBD подобийӧысь петӧ, мый сходственнӧй бокъяс пропорциональнӧйӧсь; AD/CD = CD/DB, либӧ CD² = AD∙DB, кытысь ; та дырйи кыдз тан, сідз и водзӧ босьтны кутам сӧмын арифметическӧй корень, сы вӧсна, мый кутам босьтны вундӧглысь сӧмын кузьтасӧ, а огӧй направленньӧсӧ.

3. Теорема. Быд катет эм гипотенуза костын да гипотенуза вылӧ ас проекцияыс костын средньӧй пропорциональнӧй.

Докажитӧм. 1) ACD да ABC куимпельӧсаяс подобийӧысь (245-ӧд серп.) петӧ: AB : AC = AC : AD, либӧ AC² = AB∙AD, кытысь

2) CDB да ABC куимпельӧсаяс подобийӧысь петӧ:

AB : CB = CB : DB, либӧ CB² = AB∙DB, кытысь

Следствие. Катетъяслӧн квадратъяс относитчӧны, кыдзи гипотенуза вылӧ налӧн проекцияяс.

AC² = AB∙AD да CB² = AB∙DB.

Членӧн-членӧн юкам ӧти равенствосӧ мӧдыс вылӧ, да лоӧ:

4. Теорема (Пифагорлӧн). Гипотенузалӧн квадрат равняйтчӧ катетъясса квадратъяс суммалы.

Сетӧма:

ABC куимпельӧсаын ∠C = d.

________________________

Колӧ докажитны: AC² + CB² = AB².

Докажитӧм (коймӧд). 1) AC² = AB∙AD да 2) CB² = AB∙DB. Тайӧ равенствоясӧс содтам членӧн-членӧн, да лоӧ: AC² + CB² = AB∙AD + AB∙DB = AB∙(AD + DB), но AD + DB = AB, та вӧсна AC² + CB² = AB∙AB = AB².

Веськыдпельӧса куимпельӧсаяслысь кӧ бокъяссӧ пасйыны a, b да c пыр, тайӧ теоремасӧ дженьыдджыка гижӧны со кыдз: a² + b² = c², сполнӧя лыддьӧны тадз:

Катетъяслысь кузьтаяссӧ петкӧдлысь лыдъяслӧн квадратъяс сумма равняйтчӧ гипотенузалысь кузьтасӧ петкӧдлысь лыд квадратлы.

Следствие. Катетлӧн квадрат равняйтчӧ гипотенуза да мӧд катет квадратъяс разносьтлы.

a² + b² = c², кытысь a² = c² − b², либӧ:

да b² = c² − a², либӧ: .

5. Теорема (мӧдара). Кор куимпельӧсаын a, b да c бокъяс костын эм зависимосьт a² + b² = c², сэк куимпельӧсаыс веськыдпельӧса.

Сетӧма: a, b да c — куимпельӧсалӧн бокъяс да a² + b² = c².

______________________________

Колӧ докажитны: куимпельӧсаыс — веськыдпельӧса.

Докажитӧм. Вӧчам веськыдпельӧса куимпельӧсаӧс, кодлӧн катетъясыс лоӧны a да b; гипотенузасӧ пасъям m пыр. Сэк Пифагор теорема серти: a² + b² = m². Тайӧ равенствоӧс сетӧм равенствокӧд ӧтластитӧмысь аддзам, мый c² = m² либӧ c = m. Сідзкӧ, сетӧм куимпельӧса да вӧчӧм веськыдпельӧса куимпельӧса ӧтыдждаӧсь куим бок серти, та вӧсна сетӧм куимпельӧсаыс — веськыдпельӧса.

6. Тайӧ теорема (да сылы мӧдара теорема) став геометрияса теоремаяс костын кутӧ зэв ыджыд места; сійӧс арталӧны Пифагорӧн (греческӧй философ) вӧчӧмӧн, мый вӧсна и шусьӧ Пифагор теоремаӧн. Ӧні тӧдӧны, мый тайӧ теоремаӧн определяйтчан веськыдпельӧса куимпельӧсаса бокъяс костын лыда зависимосьтсӧ тӧдісны нин египтяна, Пифагорӧс велӧдысьяс. Веськыдпельӧса куимпельӧса, кодлӧн бокъясыс 3, 4 да 5, шусьӧ египетскӧйӧн. Веськыд пельӧс вӧчӧм могысь важ землемеръяс уджавлісны татшӧм способ кузя: гӧрӧдъясӧн найӧ вӧлі юкӧны гез 12 ӧтыджда юкӧнӧ, кӧрталӧны помъяссӧ да вӧчӧны куимпельӧсаӧс, кодлӧн бокъясыс 3, 4 да 5 юкӧн кузяӧсь, сэк 3 да 4 юкӧна бокъяс костын артмӧ веськыд пельӧс.

Веськыдпельӧса куимпельӧсаяс, кодъяслӧн бокъяс муртассьӧны быдса лыдъясӧн, шусьӧны Пифагор куимпельӧсаясӧн, а асьныс лыдъясыс — Пифагор лыдъясӧн. Сідз: 3, 4 да 5; 5, 12 да 13; 6, 8 да 10; 7, 24 да 25; 8, 15 да 17; 9, 12 да 15; 10, 24 да 26 да с. в. — Пифагорлӧн лыдъяс.

3 §. Пӧлӧспельӧса куимпельӧсаын элементъяс костын метрическӧй зависимосьт.

1. Теорема. Ёсь пельӧс водзын куйлысь боклӧн квадрат мӧд кык бок квадратъяс суммаысь ичӧтджык кыкысялӧм произведенньӧӧн, коді артмӧ кутшӧмкӧ ӧти тайӧ боксӧ сы вылӧ мӧд бок проекция вылӧ ӧктӧмысь.

Сетӧма:

ABC куимпельӧсаын ∠A — ёсь;

m — c-лӧн b вылӧ проекция (246-ӧд серп.)

______________________________

Колӧ докажитны: a² = b² + c² − 2bm.

Докажитӧм. B пельӧс йылысь нуӧдам BD = h судта; артмасны веськыдпельӧса кык куимпельӧса — ABD да BDC; AD = m — AB боклӧн AC бок вылӧ проекция.

BDC куимпельӧсаысь:

a² = h² + (b − m)². (1)

ABD куимпельӧсаысь:

h² = c² − m². (2)

(1) да (2) содтам членӧн-членӧн, вӧчам колана преобразованньӧяс да лоӧ:

a² + h² = h² + (b − m)² + c² − m²;

a² = (b − m)² + c² − m²;

a² = b² − 2bm + m² + c² − m²;

a² = b² + c² − 2bm.

2. Теорема. Куимпельӧсаын тшӧтшыд пельӧс водзын куйлысь боклӧн квадрат мӧд кык бок квадратъяс суммаысь ыджыдджык кыкысялӧм произведенньӧӧн, коді артмӧ кутшӧмкӧ ӧти тайӧ боксӧ да сы нюжӧдӧм вылӧ мӧд бок проекция вылӧ ӧктӧмысь.

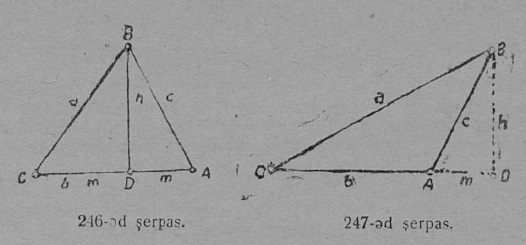
Сетӧма: ABC куимпельӧсаын ∠A — тшӧтшыд (247 серп.).

__________________________

Колӧ докажитны: a² = b² + c² + 2bm.

Докажитӧм. B йылысь AC подувтасӧс нюжӧдӧм вылӧ нуӧдам BD = h судта; артмӧны кык веськыдпельӧса куимпельӧса: BCD да ADB; AD = m — AC бокӧс нюжӧдӧм вылын AB боклӧн проекция; CD = b + m.

BCD куимпельӧсаысь:

a² = h² + (b + m)². (1)

ADB куимпельӧсаысь:

h² = c² − m². (2)

(1) да (2) содтам членӧн-членӧн, вӧчам колана преобразованньӧяс да лоӧ:

a² + h² = h² + (b + m)² + c² − m²;

a² = (b + m)² + c² − m²;

a² = b² + 2bm + m² + c² − m², либӧ

a² = b² + c² + 2bm.

3. Ёсь пельӧс водзын куйлысь бок квадрат йылысь формуласӧ тшӧтшыд пельӧс водзын куйлысь бок квадрат йылысь формулакӧд ӧтластитӧмысь аддзам, мый найӧ мӧда-мӧдысь торйӧдчӧны сӧмын бӧръя членнаныс. Кыкнан формуласӧ позьӧ ӧтлаавны ӧтиӧ; сэк лоӧ:

a² = b² + c² ± 2bm,

кӧн m — c боклӧн b бок вылӧ либӧ сійӧс нюжӧдӧм вылӧ проекция; минус пас босьтчӧ, кор определитан бокыс куйлӧ ёсь пельӧс водзын, а плюс пас — кор сійӧ куйлӧ тшӧтшыд пельӧс водзын.

4. Ёсьпельӧса ABC куимпельӧсаын (246 серп.) пондам кӧ A чут гӧгӧр гӧгӧртӧдны BA боксӧ часі стрелка движенньӧ направленньӧ кузя, ∠A кутас ыдждыны, а AB = c боклӧн AC = b бок вылӧ m проекцияыс кутас ичӧтмыны; кор, медбӧрын, ∠A пӧрӧ веськыд пельӧсӧ, проекция лоӧ нуль ыджда; миян лоӧ Пифагорлӧн теорема.

Збыльысь ӧд, a² = b² + c² − 2bm; m = 0 дырйи лоӧ: a² = b² + c².

Тшӧтшыдпельӧса ABC куимпельӧсаын (247 серп.) пондам кӧ A чут гӧгӧр гӧгӧртӧдны BA боксӧ часі стрелка движенньӧ направленньӧлы паныд, то ∠A да AB = с боклӧн m проекция кутасны ичӧтмыны; кор, медбӧрын, ∠A пӧрӧ веськыд пельӧсӧ, m проекция лоӧ нуль ыджда; миян лоӧ Пифагорлӧн теорема: a² = b² + c². Та ногӧн, Пифагорлӧн теорема — кык бӧръя теоремаяслӧн частнӧй случай.

5. Пифагор теорема серти да бӧръя кык теоремаяс серти позьӧ тӧдмавны сетӧм бокъяс кузя, кутшӧм пельӧса тайӧ куимпельӧсаыс.

ABC куимпельӧсаын кӧ:

1) a² < b² + c², куимпельӧсаыс — ёсьпельӧса;

2) a² = b² + c², куимпельӧсаыс — веськыдпельӧса;

3) a² > b² + c², куимпельӧсаыс — тшӧтшыдпельӧса.

Быд торъя случайын колӧ сӧмын ыджыдджык боклысь квадратсӧ ӧтластитны мӧд кык бок квадратъяс суммакӧд.

6. Задача. Кутшӧм сикаса куимпельӧса, кодлӧн бокъясыс 13 см, 9 см да 4 см кузяӧсь?

Решитӧм. 13² > 9² + 4², сідзкӧ, колӧ лоны, мый тайӧ куимпельӧсаыс — тшӧтшыдпельӧса.

Но задачаын сетӧмъяс кузя вӧчны куимпельӧсаӧс он вермы сы вӧсна, мый куимпельӧсаӧс вӧчӧм вылӧ условийӧ серти колӧ, медым ыджыдджык бок вӧлі мӧд кык бок суммаысь ичӧтджык; тан условийӧыс оз соблюдайтчы: 13 = 9 + 4, ыджыдджык бок мӧд кык бок сумма ыджда, та дырйи куимпельӧса оз артмы.

Тайӧ задачалӧн анализ петкӧдлӧ, мый, кутшӧм сикаса лоӧ сетӧм бокъяс серти куимпельӧса, шуӧм водзын колӧ видзӧдлыны, позьӧ-ӧ задачаын сетӧмъяс кузя вӧчны куимпельӧсасӧ.

Та ногӧн, 13² > 9² + 4² условийӧ — необходимӧй (колана) условийӧ, мый тшӧтшыдпельӧса куимпельӧса вермас лоны, но абу достаточнӧй (тырмана) условийӧ. Кыкнан условийӧ: 1) 13² > 9² + 5² да 2) 13 < 9 + 5, кор найӧс босьтан ӧттшӧтш, тырмӧны (достаточнӧйӧсь) шуны, мый куимпельӧсаыс — тшӧтшыдпельӧса.

4 §. Параллелограммлӧн бокъяс да диагональяс костын зависимосьт.

Теорема. Параллелограммын диагональяс квадратъяслӧн суммаыс равняйтчӧ доръясыс квадратъяс суммалы.

Сетӧма: ABCD — параллелограмм;

AB ∥ CD да AD ∥ BC (248-ӧд серпас).

__________________________________

Колӧ докажитны:

AC² + BD² = AB² + BC² + CD² + AD².

Докажитӧм. ABCD параллелограммын D да C йывъяссянь нуӧдам DE да CF судтаяс; лоӧны веськыдпельӧса DAE да CBF куимпельӧсаяс; налӧн DA = CB да ∠A = ∠CBF, сідзкӧ, найӧ ӧтыдждаӧсь, та вӧсна AE = BF.

∆ABC-ысь:

AC² = AB² + BC² + 2AB∙BF. (1)

∆ABD-ысь:

BD² = DA² + AB² − 2AB∙AE. (2)

Бӧръя равенствоысь AB² вежам CD²-ӧн да AE BF-ӧн; сэсся (1) да (2) равенствояссӧ членӧн-членӧн содтам, да лоӧ:

AC² + BD² = AB² + BC² + CD² + DA².

5 §. Куимпельӧсалысь судтасӧ да медианасӧ арталӧм.

Задача 1. Артавны куимпельӧсалысь m_a медианасӧ, кор сетӧма сылысь бокъяс: a, b да c (249-ӧд серпас).

Решитӧм. ABC куимпельӧсаын нуӧдам AD = m_a медиана, сійӧс нюжӧдӧм вылӧ пуктам DE = AD да E чутсӧ ӧтлаалам B да C чутъяскӧд; лоӧ ABEC параллелограмм, кодлӧн бокъясыс — b да c, диагональ BC = a да диагональ AE = 2m_a.

Параллелограммса диагональяс да бокъяс зависимосьт серти лоӧ:

(2m_a)² + a² = b² + b² + c² + c², либӧ

4m_a² + a² = 2b² + 2c²; либӧ 4m_a² = 2b² + 2c² − a², кытысь

m_a² = (2b² + 2c² − a²)/4, либӧ

Аналогия кузя:

да

Задача 2. Артавны куимпельӧсалысь h_b судтасӧ, кор сылысь сетӧма бокъяссӧ: a, b да c (250-ӧд серпас).

Решитӧм. Куимпельӧсаса B йывсянь нуӧдам BD = h_b судта да AD пасъям m-ӧн.

∆ABD-ысь:

h_b² = c² − m². (1)

m колӧ вежны сэтшӧм выраженньӧӧн, кытчӧ медым пырисны куимпельӧсалӧн a, b да c бокъяс. ∆ABC-ысь:

a² = b² + c² − 2bm,

кытысь корсям

m = (b² + c² − a²)/2b. (2)

m-лы сюрӧм (2) выраженньӧсӧ пуктам (1) равенствоӧ, лоӧ:

h_b² = c² − (b² + c² − a²)²/(2b)²,

либӧ

h_b² = ((2bc)² − (b² + c² − a²)²)/(2b)². (3)

(3) дроблысь числительсӧ прӧстӧй ӧктасъясӧ разложитӧм бӧрын лоӧ:

h_b² = (2bc + b² + c² − a²)∙(2bc − b² − c² + a²)/(2b)²,

либӧ

h_b² = [(b + c)² − a²]∙[a² − (b − c)²]/(2b)².

Сэсся разложитам ӧктасъясӧ квадратнӧй скобкаяс пытшкӧс выраженньӧяссӧ; лоӧ:

h_b² = (b + c + a)∙(b + c − a)∙(a + b − c)∙(a + c − b)/(2b)². (4)

Куимпельӧсалысь периметрсӧ пасъям 2p-ӧн: a + b + c = 2p, сэк:

b + c = 2p − a, b + c − a = 2p − a − a = 2(p − a);

a + b = 2p − c, a + b − c = 2p − c − c = 2(p − c);

a + c = 2p − b, a + c − b = 2p − b − b = 2(p − b). (5)

(4) равенствоын ӧктасъяссӧ вежам (5) равенствоын артмӧм выраженньӧясӧн, да лоӧ:

h_b² = 2p∙2(p − a)∙2(p − b)∙2(p − c)/4b²,

кытысь

Аналогия кузя:

Колӧ нӧшта докажитны, мый некутшӧм ӧктас p − a, p − b, p − c ӧктасъяс костысь оз ло отрицательнӧйӧн; лоӧ кӧ отрицательнӧйӧн наысь кодкӧ ӧти, h лоӧ мнимӧй лыдӧн.

Любӧй куимпельӧсаын ӧти бок мӧд кык бокъяс суммаысь ичӧтджык, та вӧсна a < b + c. Кыкнан пай дінӧ неравенствоӧ a-ӧн содтӧмысь лоӧ: 2a < b + c + a, либӧ 2a < 2p, кытысь a < p; та вӧсна p − a = положительнӧй лыд; дзик жӧ тадз p − b да p − c положительнӧй лыдъяс; та ногӧн, корень увса выраженньӧ — положительнӧй лыд.

6 §. Куим бок серти куимпельӧсалысь площадьсӧ тӧдмалӧм. Геронлӧн формула.

Задача. a, b да c бокъяс серти тӧдмавны ABC куимпельӧсалысь площадь.

Решитӧм. S∆ = ½a∙h_a, но

кӧн p — куимпельӧсалӧн периметр джын, сідзкӧ,

либӧ

квадрата единица.

Тайӧ формула шусьӧ Герон формулаӧн, Александрияса греческӧй математик Герон ним кузя.

Юасянъяс да упражненньӧяс.

1. Позьӧ-ӧ вӧчны веськыдпельӧса куимпельӧсаӧс, кор тӧдам: 1) сӧмын гипотенузалысь кузьта, 2) вундӧгъяс, кодъясӧ вундыссьӧ гипотенуза веськыд пельӧс йывсянь нуӧдӧм судтаӧн?

2. Кутшӧм сикас куимпельӧса лоӧ пельӧсъяс серти, кор сылӧн бокъясыс: 1) 4 см, 5 см, 6 см; 2) 10 см, 6 см, 4 см кузьтаӧсь?

3. Веськыдпельӧса куимпельӧсаын h судта 8 см кузьта да ӧти катетыслӧн гипотенуза вылӧ проекция 6 см ыджда. Тӧдмавны куимпельӧсалысь бокъяссӧ.

4. Кык вын — 3,2 кг да 2,4 кг — пуктӧма ӧти сійӧ жӧ чут бердӧ да направитӧма мӧда-мӧдлы веськыд пельӧс улын. Корсьны налысь равнодействующӧйсӧ.

5. Куимпельӧсалӧн бокъяс 8 см, 10 см да 11 см. Артавны медианаяссӧ да судтаяссӧ.

XVIII. КРУГЫН ПРОПОРЦИОНАЛЬНӦЙ ВУНДӦГЪЯС

1 §. Кытшвизьвывса чутысь диаметр вылӧ нуӧдӧм перпендикулярлӧн свойство.

1. Теорема. Кытшвизьвывса кутшӧмкӧ чутысь диаметр вылӧ нуӧдӧм перпендикуляр эм диаметр вундӧгъяс костын средньӧй пропорциональнӧй, а кык пиысь быд хорда, кодъяс тайӧ чутсӧ ӧтлаалӧны диаметр помъяскӧд, эм диаметр да сы вылӧ хорда проекция костын средньӧй пропорциональнӧй.

Сетӧма:

AB — диаметр; CD ⊥ AB; AC да CB — хордаяс

(251 серп.).

________________________________

Колӧ докажитны:

1) AD/CD = CD/DB; 2) AB/AC = AC/AD; 3) AB/CB = CB/DB.

Докажитӧм. Сы вӧсна, мый ∠C сиптыссьӧ диаметрӧн, ABC куимпельӧса — веськыдпельӧса; CD — сылӧн судта, AD да DB — хордаяслӧн (катетъяслӧн) диаметр (гипотенуза) вылӧ проекцияяс, та вӧсна:

1) AD/CD = CD/DB; 2) AB/AC = AC/AD; 3) AB/CB = CB/DB.

2. Задача 1. Вӧчны кык сетӧм a да b вундӧгъяс костса средньӧй пропорциональнӧй x вундӧгӧс (252-ӧд серпас).

Построенньӧ. MN веськыд визь вылӧ кутшӧмкӧ A чутсянь пукталам водзысь-водзӧ вундӧгъяс: AD = a да DB = b. AB босьтам диаметр пыдди, нуӧдам сы вылӧ кытшвизь джын да D чутын AB-лы DC перпендикуляр, кытшвизькӧд C чутын вомӧнасьтӧдз, коді лоӧ корсян x вундӧгӧн.

Збыльысь ӧд, a : x = x : b, либӧ x² = ab, кытысь .

Задача 2. Докажитны, мый кык абу ӧтыджда a да b лыдлӧн среднӧй арифметическӧй сійӧ жӧ лыдъяс средньӧй геометрическӧйысь ыджыдджык.

Решитӧм. Кык абу ӧтыджда вундӧгъяс мед соответствуйтӧны a да b лыдъяслы (252 серпас). Вӧчам a да b лыдъяслысь средньӧй геометрическӧй: .

a да b лыдъяслӧн (a + b)/2 средньӧй арифметическӧй, кыдз тыдалӧ серпас вылысь, (AD + DB)/2 = AO = r ыджда. Сідзкӧ,

Но CO сідзжӧ r ыджда. Веськыдпельӧса COD куимпельӧсаысь петӧ, мый CO > CD. CO = (a + b)/2 да , та вӧсна

— кык абу ӧтыджда лыдлӧн средньӧй арифметическӧй сійӧ жӧ лыдъясса средньӧй геометрическӧйысь ыджыдджык.

Кор b = a, CD = CO сы вӧсна, мый сэк

либӧ a = a.

2 §. Вомӧнасян хордаяс вундӧгъяслӧн свойство.

Теорема. Сетӧм кытшвизьлӧн кык хорда либӧ некымын хорда вомӧнасьӧны кӧ ӧти чутын, любӧй хордаса вундӧгъяслӧн произведенньӧ — постояннӧй величина, коді равняйтчӧ сійӧ жӧ чут пыр мунысь сетӧм кытшвизьса диаметр вундӧгъяс произведенньӧлы.

Сетӧма: AB да CD — хордаяс; EF — диаметр;

P — налӧн вомӧнасянін чут (253 серп.)

________________________________

Колӧ докажитны: PA∙PB = PC∙PD = PE∙PF.

Докажитӧм. Нуӧдам отсасьысь AC да BD хордаяс. Лоӧны кык куимпельӧса: APC да BPD; найӧ ӧтыджда пельӧсаӧсь: ∠A = ∠D да ∠C = ∠B кыдз ӧти сійӧ жӧ дугаясӧн муртассян вписаннӧй пельӧсъяс. Сідзкӧ тайӧ куимпельӧсаяс подобнӧйӧсь, кытысь петӧ, мый:

PA : PC = PD : PB,

либӧ

PA∙PB = PC∙PD.

Босьтны кӧ AB хордаӧс да EF диаметрӧс кыдз кык вомӧнасян хордаясӧс, докажитӧм серти лоӧ:

PA∙PB = PE∙PF.

Тадз жӧ лоӧ P чут пыр мунысь любӧй хордакӧд; та вӧсна сетӧм кытшвизьын сійӧ жӧ ӧти чут пыр мунысь быд хордаса вундӧгъяслӧн произведенньӧ — постояннӧй величина, коді сійӧ жӧ чут пыр мунысь диаметр вундӧгъяс произведенньӧ ыджда.

3 §. Круг сайын вомӧнасьысь вундысьяслӧн свойство.

1. Ортсыс A чутысь нуӧдӧма AB вундысьӧс (254 серп.). Вундысьлӧн кытшвизь пытшкӧсса юкӧныс — BC хорда; ортсыс A чутӧдз кытшвизь сайӧ сылӧн нюжӧдӧмыс шусьӧ вундысь визь ортсыс юкӧнӧн. Кыкнан вундӧглӧн сумма: BC + CA = AB — вундысьлӧн кузьта.

2. Теорема. Круг сайса ӧти сійӧ жӧ чутысь кӧ нуӧдӧма вундысьясӧс да касательнӧйӧс, быд вундысьлӧн ас ортсыс юкӧныс вылӧ произведенньӧ — постояннӧй величина, касательнӧй визь квадрат ыджда.

Сетӧма: PA да PC — вундысьяс; PK — касательнӧй;

P — налӧн вомӧнасянін чут (255 с.)

__________________________________

Колӧ докажитны: PA∙PB = PC∙PD = PK².

Докажитӧм. PA да PC — вундысьяс, PB да PD — налӧн ортсыс юкӧнъясыс. Нуӧдам отсасьысь AD да BC хордаяс, артмасны кык куимпельӧса — ADP да BCP. Тайӧ куимпельӧсаясын эмӧсь соответственнӧя ӧтыджда кык пельӧсӧн: ∠A = ∠C кыдз ӧти сійӧ жӧ BD дуга джынӧн муртассян вписаннӧй пельӧсъяс да ∠P — ӧтувъя; тайӧ куимпельӧсаяс, кыдз ӧтыджда пельӧсаяс, подобнӧйӧсь, мый вӧсна: PA/PD = PC/PB либӧ PA∙PB = PD∙PC.

PC вундӧгӧс кӧ P чут гӧгӧр кутам гӧгӧртӧдны сідз, медым сійӧ воас PK касательнӧй положенньӧӧ, вундысьлӧн кытшвизькӧд вомӧнасянін C да D чутъяс кутасны мӧда-мӧдыс дінӧ матысмыны, PC вундысь кутас ичӧтмыны, а ортсыс PD пайыс — ыдждыны; касанньӧ K чутын и вундысь и сылӧн ортсыс пайыс лоӧны PK касательнӧй ыджда, та вӧсна PA∙PB = PC∙PD равенствоын PC да PD вундӧгъясӧс PK вундӧгӧн вежӧм бӧрын лоӧ:

PA∙PB = PK∙PK либӧ PA∙PB = PK².

Та ногӧн:

PA∙PB = PC∙PD = PK².

Тадз жӧ лоӧ P чутысь нуӧдӧм любӧй вундыськӧд, та вӧсна круг сайса ӧти сійӧ жӧ чутысь нуӧдӧм став вундысьяслӧн ас ортсыс юкӧнныс вылӧ произведенньӧ лоӧ постояннӧй величинаӧн да равняйтчӧ сійӧ жӧ чутысь нуӧдӧм касательнӧй визь квадратлы.

3. Следствие. Круг сайса ӧти сійӧ жӧ чутысь кӧ нуӧдӧма касательнӧйӧс да вундысьӧс, касательнӧйыс эм дзоньнас вундысьыс да сылӧн ортсыс юкӧныс костын средньӧй пропорциональнӧй.

PA∙PB = PK²; сідзкӧ, PA : PK = PK : PB.

4 §. Крайней да средней отношенньӧын вундӧгӧс юкӧм.

1. Вундӧг крайней да средней отношенньӧын юкӧм лоӧ сійӧ, мый вундӧг вылысь колӧ корсьны сэтшӧм чут, кӧн медым вундӧг юксяс кык сэтшӧм юкӧнӧ, мед ыджыдджык юкӧныс лоас став вундӧг да ичӧтджык юкӧн костас средньӧй пропорциональнӧйӧн.

2. Задача. Сетӧм вундӧгӧс юкны крайней да средней отношенньӧӧн.

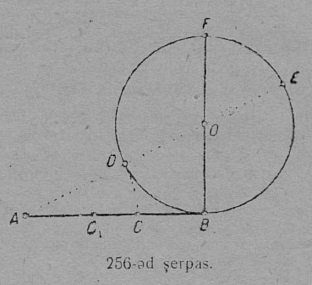
Решитӧм. AB = a — сетӧм вундӧг. Медым C чут — корсян чут (256-ӧд серпас). Вундӧглысь ыджыдджык юкӧнсӧ пасъям x-ӧн: AC = x, сэк ичӧтджык юкӧныс CB = a − x. Задача условийӧ серти колӧ лоны a/x = x/(a − x), либӧ x² = a(a − x), либӧ x² = a² − ax.

Гижам тайӧ равенствосӧ тадз: a² = x² + ax, кытысь a² = x(a + x).

AB = a вундӧгӧс босьтам кутшӧмкӧ кытшвизь бердса касательнӧй пыдди, a + x — вундысь пыдди, а x — сы ортсыс пайыс пыдди; таысь ӧтдор, шуам, вундысь медым мунӧ шӧрчут пыр, сэк AB = a — кытшвизьлӧн диаметр.

Построенньӧ. AB = a босьтам касательнӧй пыдди, а B чут — касанньӧ чут пыдди; B чутын AB-лы нуӧдам перпендикуляр да сы вылӧ пуктам a ыджда BF вундӧг — кытшвизьлысь диаметр; BF-ӧс юкам шӧри, сюрӧ O шӧрчут да OB радиусӧн нуӧдам кытшвизь, сэсся O шӧрчут пыр нуӧдам AE вундӧгӧс; сэк AE вундӧглӧн ортсыс AD юкӧныс лоӧ x ыджда. AB вылӧ пуктам AC = AD вундӧг, сэк AB вундӧг вылын сюрӧ корсян C чут, коді сійӧс юкӧ крайней да средней отношенньӧӧн.

Тайӧ та вӧсна, мый AE∙AD = AB²; но AE = a + x, AD = x да AB = a, та вӧсна (a + x)x = a², либӧ ax + x² = a², кытысь

x² = a² − ax = a(a − x),

мый сетӧ a : x = x : (a − x).

Отсасьысь кытшвизь кӧ вӧчны AB вундӧг бердӧ A чутын касайтчысьӧсь, AB вундӧг вылын лоӧ нӧшта ӧти C₁ чут, коді сідзжӧ AB вундӧгӧс юкас крайньӧй да средней отношенньӧӧн.

Тадз, AB вундӧг вылын эм кык чут, кодъяс сійӧс юкӧны крайней да средней отношенньӧӧн. Тайӧ C да C₁ чутъяс AB вундӧглӧн шӧр серти куйлӧны симметричнӧя. Вылын сюрӧм a² = x² + ax равенствоӧс позьӧ гижны тадз: x² + ax − a² = 0; тайӧ уравненньӧӧс x серти решитӧм бӧрын сюрӧ:

Сы вӧсна, мый ми босьтам сӧмын x вундӧглысь кузьта, а направленньӧсӧ огӧй, уравненньӧлысь отрицательнӧй кореньсӧ шыбитӧм бӧрын лоӧ:

либӧ

Тайӧ петкӧдлӧ, мый x вундӧг эм a/2 да a катетъяса веськыдпельӧса ABO куимпельӧсаса гипотенуза да сетӧм a вундӧглӧн джын (OD вундӧг) костса разносьт: x = AO − OD = AD = AC (256-ӧд серпас).

x-лы сюрӧм выраженньӧ пӧрӧ:

либӧ x ≈ 0,62a. Сідзкӧ, AC : CB ≈ 5 : 3.

Юасянъяс да упражненньӧяс.

1. Кытшвизьлӧн диаметр P чутӧн юксьӧ 4 см да 6 см ыджда юкӧнъясӧ. Мый вӧсна сійӧ жӧ чут пыр оз позь нуӧдны сэтшӧм хорда, мед сылӧн ӧти юкӧныс вӧлі 3 см ыджда?

2. Кытшвизьын вомӧнасьӧны кык хорда. Ӧтиыслӧн юкӧнъясыс 6 см да 25 см ыдждаӧсь; мӧд хордалӧн вундӧгъяс относитчӧны кыдз 1 : 2. Корсьны мӧд хордалысь кузьтасӧ.

3. Хорда 5 см ыджда. Кузя-ӧ колӧ сійӧс нюжӧдны, медым нюжӧдӧм вундӧг помсянь нуӧдӧм касательнӧй волі 6 см ыджда?

4. R радиуса кругын нуӧдӧма радиуслы перпендикулярнӧя да сы шӧрӧд мунысь хорда. Корсьны хордалысь кузьта да определитны, кутшӧм юкӧн лоӧ кытшвизьлӧн хордаӧн стягивайтан дуга.

XIX. ВПИСАННӦЙ ДА ОПИСАННӦЙ УНАПЕЛЬӦСАЯС.

1 §. Вписаннӧй да описаннӧй куимпельӧсаяс.

1. Унапельӧса, кодлӧн став йылыс куйлӧны кытшвизь вылын, шусьӧ вписаннӧйӧн, а ачыс кытшвизьыс — описаннӧйӧн. ABCDE — вписаннӧй витпельӧса (257-ӧд серпас). Сылӧн бокъясыс — AB, BC, CD... — сетӧм кытшвизьлӧн хордаяс.

Унапельӧса, кодлӧн став бокыс касайтчӧны кытшвизьӧ, шусьӧ описаннӧйӧн, а ачыс кытшвизьыс — вписаннӧйӧн. ABCDE — описаннӧй витпельӧса (258-ӧд серпас). Сылӧн бокъяс — AB, BC, CD... — кытшвизьӧ касательнӧйяс.

2. Теорема. Быд куимпельӧсаса куим йыв пыр позьӧ нуӧдны кытшвизь да сӧмын ӧтиӧс.

A, B да C — куим чут, кодъяс ABC куимпельӧсалӧн йывъяс, оз куйлыны ӧти веськыд визь вылын, та вӧсна на пыр позьӧ нуӧдны кытшвизь да сӧмын ӧтиӧс.

Описаннӧй кытшвизьлӧн шӧрчут куйлӧ куимпельӧсаса кык любӧй бок шӧр пыр нуӧдӧм перпендикуляръяслӧн вомӧнасянін чутын. Перпендикуляр, кодӧс нуӧдӧма коймӧд боклы шӧрыс пыр, сідзжӧ мунӧ описаннӧй кытшвизь шӧрчут пырыс.

Следствие. Перпендикуляръяс, кодъясӧс нуӧдӧма куимпельӧсаса бокъяслы шӧръяс пырыс, вомӧнасьӧны ӧти чутын — описаннӧй кытшвизь шӧрчутын.

Описаннӧй кытшвизьлӧн шӧрчут куйлӧ:

1) куимпельӧса пытшкын, кор куимпельӧсаыс ёсьпельӧса (259-д серпас); 2) гипотенуза вылын (шӧрас), кор куимпельӧсаыс — веськыдпельӧса (260 серп.); 3) куимпельӧса сайын, кор куимпельӧсаыс — тшӧтшыдпельӧса (261 серп.).

3. Теорема. Быд куимпельӧсаӧ позьӧ впишитны кытшвизь да сӧмын ӧтиӧс.

Сетӧма: ∆ABC (262 серп.)

________________________________

Колӧ докажитны: ∆ABC-ӧ позьӧ впишитны кытшвизь да сӧмын ӧтиӧс.

Докажитӧм. Куимпельӧсаӧ кытшвизьӧс впишитӧм лоӧ сійӧ, мый колӧ корсьны шӧрчутыслысь местасӧ да радиусыслысь кузьта. ABC куимпельӧса бокъяслы колӧ лоны корсян кытшвизьӧ касательнӧйясӧн; ӧти сійӧ жӧ кытшвизьын касательнӧйяс шӧрчутсянь радиус ылнаынӧсь, та вӧсна вписаннӧй кытшвизьлысь шӧрчутӧс корсьӧм вылӧ колӧ корсьны сэтшӧм чут, медым сійӧ вӧлі куимпельӧсаса бокъяссянь ӧтылнаын.

Куимпельӧса бокъяссянь ӧтылнаӧ ылӧсмӧм чут лоӧ куимпельӧсаын любӧй кык биссектриса вомӧнасянін O чут; O чутыс и лоӧ шӧрчутӧн кытшвизьын, кодӧс впишитӧма куимпельӧсаӧ; тайӧ кытшвизьлӧн радиусыс лоӧ любӧй перпендикуляр, кодӧс нуӧдӧма O шӧрчутсянь куимпельӧса боклы, — OK, OM либӧ ON. Куимпельӧсалӧн бокъяс, кодъяс OK, OM да ON радиусъяслы перпендикулярнӧйӧсь да мунӧны кытшвизь вылын куйлысь K, M да N помъясыс пыр, лоӧны кытшвизьлы касательнӧйясӧн.

Сійӧ жӧ ABC куимпельӧсаӧ вписаннӧй мӧд кытшвизь лоны оз вермы сы вӧсна, мый куимпельӧсаын кык пельӧслӧн биссектрисаяс вомӧнасьӧны сӧмын ӧти чутын. O чут, кыдз BC да AC бокъяссянь ӧтылнаӧ ылысмӧдӧм чут, куйлӧ сідзжӧ ∠C биссектриса вылын.

4. Тӧдана, мый O чут кындзи эм нӧшта куим чут, кодъяс ӧтылнаынӧсь куимпельӧса куимнан боксяньыс, да кодъяс куйлӧны куимпельӧса ортсыын. Тайӧ куим чутыс лоӧны шӧрчутъясӧн куим кытшвизьлы, кодъяс пиысь быдӧн касайтчӧ куимпельӧсаса ӧти бокӧ да мӧд кык бокъясса нюжӧдӧмъясӧ. Татшӧм кытшвизьяс шусьӧны вневписаннӧйясӧн (215 серпас 115 листбок).

Сідзкӧ, куимпельӧса дорӧ относитчӧм серти ми торйӧдалам: 1) ӧти описаннӧй кытшвизь, коді мунӧ куимпельӧсаса куимнан йыв пырыс; 2) ӧти вписаннӧй кытшвизь, коді касайтчӧ куимпельӧсаса куимнан бокас, да 3) куим вневписаннӧй кытшвизь.

2 §. Вписаннӧй нёльпельӧсаын пельӧсъяслӧн свойствояс.

1. Теорема. Быд вписаннӧй нёльпельӧсаын воча куйлысь пельӧсъяслӧн суммаыс кык веськыд пельӧс ыджда.

Сетӧма: ABCD — вписаннӧй нёльпельӧса (263 серпас).

_________________________________

Колӧ докажитны: ∠A + ∠C = 2d да ∠B + ∠D = 2d.

Докажитӧм. ∠A кыдз вписаннӧй муртассьӧ ‿DCB/2 да ∠C муртассьӧ ‿BAD/2, сідзкӧ A да C пельӧсъяслӧн сумма муртассьӧ суммаӧн: ‿DCB/2 + ‿BAD/2, либӧ (‿DCB + ‿BAD)/2 — кытшвизь джынӧн, та вӧсна ∠A + ∠C = 180° = 2d.

Тадзи жӧ докажитӧны, мый ∠B + ∠D = 2d.

2. Теорема (мӧдара). Нёльпельӧсаын кӧ воча куйлысь пельӧсъяслӧн сумма 2d ыджда, йывъяс пырыс позьӧ нуӧдны кытшвизь.

Сетӧма: ABCD — нёльпельӧса (263 серп.)

∠A + ∠C = 2d да ∠B + ∠D = 2d.

____________________________

Колӧ докажитны: ABCD нёльпельӧсаса A, B, C да D йывъяс пыр позьӧ нуӧдны кругкытш.

Докажитӧм. ABCD нёльпельӧсаса куим йыв пыр — A, B да C — нуӧдам кытшвизь. Докажитам, мый тайӧ кытшвизьыс мунас сідзжӧ нёльӧд D йыв пыр. Шуам кӧ, мый D чут оз куйлы кытшвизь вылын, а куйлӧ кӧнкӧ круг пытшкын либӧ круг сайын, ∠D оз понды муртассьыны ABC дуга джынӧн; сідзкӧ, сэк лоӧ, мый B да D пельӧсъяслӧн сумма абу 2d ыджда, тайӧ паныдасьӧ условийӧлы; та вӧсна D чутлы колӧ куйлыны кытшвизь вылын; а тайӧ лоӧ, мый A, B да C чутъяс пыр мунысь кытшвизь мунас сідзжӧ D чут пыр. ABCD нёльпельӧса — вписаннӧй нёльпельӧса.

3. Вписаннӧйясӧн вермасны лоны веськыднёльпельӧса, квадрат да кык ӧткузя бока трапеция сы вӧсна, мый тайӧ нёльпельӧсаяслӧн воча куйлысь пельӧсъяслӧн суммаыс 2d ыджда.

3 §. Описаннӧй нёльпельӧсаын бокъяслӧн свойствояс.

1. Теорема. Описаннӧй нёльпельӧсаын воча куйлысь кык боклӧн сумма равняйтчӧ мӧд кык бок суммалы.

Сетӧма: ABCD — описаннӧй нёльпельӧса (264 серп.).

_______________________________

Колӧ докажитны: AD + BC = AB + DC.

Докажитӧм. Описаннӧй нёльпельӧсалӧн бокъясыс — кытшвизьӧ касательнӧйяс. Ӧти сійӧ жӧ чутысь кытшвизь бердӧ нуӧдӧм 2 касательнӧй ӧтыдждаӧсь; та вӧсна AN = AK, BL = BK, CL = CM, DN = DM. Тайӧ равенствоясӧс членӧн-членӧн содтӧмысь петӧ:

AN + DN + BL + CL = AK + BK + CM + DM,

либӧ

AD + BC = AB + DC.

2. Нёльпельӧсаӧ впишитны кытшвизьӧс позьӧ сӧмын сэк, кор воча куйлысь кык боклӧн суммаыс равняйтчӧ мӧд кык бок суммалы.

Став параллелограммъяс пиысь кытшвизьӧс позьӧ впишитны сӧмын ромбӧ, сідзкӧ и квадратӧ тшӧтш.

4 §. Описаннӧй унапельӧсалӧн да куимпельӧсалӧн площадь.

1. Теорема. Описаннӧй унапельӧсалӧн площадь равняйтчӧ периметрыслӧн вписаннӧй кытшвизь радиус вылӧ произведенньӧ джынлы.

Сетӧма: ABCDE — описаннӧй n-пельӧса;

r — вписаннӧй кытшвизьлӧн радиус;

P_n — n-пельӧсалӧн периметр (265-ӧд серпас).

____________________________

Колӧ докажитны: сылӧн площадь S_n = ½P_n∙r.

Докажитӧм. Кытшвизьлысь O шӧрчутӧс ABCDE унапельӧсаса йывъяскӧд ӧтлаалӧмӧн унапельӧса торйӧдчӧ n куимпельӧсаяс вылӧ.

∆ABO пл. = ½AB∙r; ∆BOC пл. = ½BC∙r

................................

................................

______________________________

∆ABO пл. + ∆BOC пл. + ... = ½r∙(AB + BC + ...);

сідзкӧ, S_n = ½r∙P_n, либӧ S_n = ½P_n∙r.

2. Следствие. Описаннӧй куимпельӧсалӧн площадь S∆ = p∙r, кӧн p — куимпельӧсалӧн периметр джын.

3. Задача. Куимпельӧсалӧн бокъяс a, b да c. Тӧдмавны вписаннӧй кытшвизьлысь r радиус.

Решитӧм. S∆ = p∙r, сідзкӧ, r = S∆/p, но Герон формула кузя

та вӧсна

Юасянъяс да упражненньӧяс.

1. Мый вӧсна оз позь кытшвизьӧс нуӧдны нёльпельӧсаса став бокъяс пыр, кор бокъясыс мӧда-мӧдыскӧд относитчӧны, кыдз 2 : 3 : 4 : 5?

2. Мый вӧсна оз позь нёльпельӧсаӧ впишитны кытшвизь, кор бокъяс мӧда-мӧдыскӧд относитчӧны, кыдз 1 : 2 : 3 : 4?

3. Вӧчны ABC куимпельӧсаӧс, кор сетӧма b да c бокъяс да R — описаннӧй кытшвизьлӧн радиус.

4. Вӧчны ABC куимпельӧсаӧс, кор сетӧма: a бок, ∠B да R — описаннӧй кытшвизьлӧн радиус.

5. Вӧчны ABC куимпельӧсаӧс, кор сетӧма: c бок, ∠A да r — вписаннӧй кытшвизьлӧн радиус.

6. Вӧчны ABC куимпельӧсаӧс, кор сетӧма: ∠A да ∠B да r — вписаннӧй кытшвизьлӧн радиус.

7. Вӧчны кык ӧткузя бока куимпельӧсаӧс, кор сетӧма: a подувтас да R — описаннӧй кытшвизьлӧн радиус.

8. Вӧчны ромб a бок да вписаннӧй кытшвизьса r радиус серти.

9. Описаннӧй нёльпельӧсалӧн последовательнӧй пӧрадокӧн босьтӧмӧн куим бокыс — 6 см, 4 см да 5 см ыдждаӧсь. Тӧдмавны нёльӧд боксӧ.

10. Любӧй куимпельӧсаын a∙b = 2R∙h_c, кӧні R — описаннӧй кытшвизьлӧн радиус. Докажитны.

11. ab = 2R∙h_c формулаӧн пӧльзуйтчӧмӧн петкӧдлыны, мый R = abc/4S, либӧ S = abc/4R, кӧні S — куимпельӧсалӧн площадь.

XX. ПРАВИЛЬНӦЙ УНАПЕЛЬӦСАЯС.

1 §. Правильнӧй унапельӧсаяс.

1. Унапельӧса, кодлӧн 1) став бокыс ӧтыджда да 2) став пельӧсыс ӧтыджда, шусьӧ правильнӧйӧн.

Ӧткузя бокъяса куимпельӧса да квадрат — правильнӧй унапельӧсаяс вылӧ примеръяс. Веськыднёльпельӧсаӧс либӧ ромбӧс правильнӧй унапельӧсаӧн шуны оз позь, — веськыднёльпельӧсалӧн став пельӧсыс ӧтыджда, а бокъясыс абу ӧтыдждаӧсь, ромблӧн став бокыс ӧтыджда, а пельӧсъясыс абу ӧтыдждаӧсь.

2. n-пельӧсаын пытшкӧс пельӧсъяслӧн сумма 2d(n − 2) ыджда, сідзкӧ правильнӧй n-пельӧсаын быд пытшкӧс пельӧс 2d(n − 2)/n ыджда. Любӧй n-пельӧсаын ортсыс пельӧсъяслӧн суммаыс 4d ыджда, та вӧсна правильнӧй n-пельӧсаын быд ортсыс пельӧс 4d/n ыджда.

Правильнӧй n-пельӧсалысь пытшкӧс пельӧссӧ позьӧ артавны орчча пельӧсыс кузя:

пытшкӧс пельӧс = 2d − 4d/n =2d(1 − 2/n).

3. Правильнӧй n-пельӧсалӧн кӧ бокыс a ыджда, периметрыс лоӧ P = an.

Ӧтлыда бокъяса унапельӧсаяс шусьӧны ӧтинимаясӧн.

Правильнӧй ӧтинима унапельӧсаяс равнӧйӧсь, кор налӧн бокъясыс равнӧйӧсь.

2 §. Правильнӧй вписаннӧй да описаннӧй унапельӧсаясӧс вӧчӧм.

1. Теорема. Кытшвизьӧс кӧ юкӧма ӧтыджда юкӧнъясӧ произвольнӧй лыд вылӧ, 1) юкан чутъясӧс водзысь-водзӧ ӧтлаалысь хордаяс вӧчӧны правильнӧй вписаннӧй унапельӧсаӧс; 2) юкан чутъяс пыр нуӧдӧм касательнӧйяс артмӧдӧны правильнӧй описаннӧй унапельӧса.

Сетӧма: O кытшвизьӧс A, B, C... чутъясын юкӧма n ӧтыджда юкӧнӧ (266 серпас).

___________________________

Колӧ докажитны: 1) AB, BC, CD... хордаяс артмӧдӧны правильнӧй вписаннӧй унапельӧсаӧс да

2) KL, LM, MN... — правильнӧй описаннӧй унапельӧса.

Докажитӧм. 1) Кытшвизьӧс юкан чутъясӧс водзысь-водзӧ хордаясӧн ӧтлаалӧм бӧрын лоӧ вписаннӧй ABCDEF унапельӧса. AB, BC, CD... дугаяс ӧтыдждаӧсь, та вӧсна найӧс стягивайтан хордаяс сідзжӧ ӧтыдждаӧсь: AB = BC = CD... Таысь ӧтдор, ∠A = ∠B = ∠C = ... кыдз ӧтыджда дугаясӧн муртассян вписаннӧй пельӧсъяс, та вӧсна вписаннӧй ABCDEF унапельӧса, кодлӧн бокъясыс да пельӧсъясыс ӧтыдждаӧсь, — правильнӧй.

2) Кытшвизьӧс юкан A, B, C, D... чутъяс пыр касательнӧйясӧс нуӧдӧм бӧрын артмас описаннӧй KLMNPQ унапельӧса. AKB, BLC, CMD... куимпельӧсаяслӧн AB, BC, CD... подувтасъяс ӧтыдждаӧсь, подувтас бердса KAB, KBA, LBC, LCB... пельӧсъяс кыдз ӧтыджда дугаясӧн муртасян пельӧсъяс сідзжӧ ӧтыдждаӧсь; сідзкӧ, куимпельӧсаяс 1) кык ӧткузя бокаӧсь да 2) ӧтыдждаӧсь.

Куимпельӧсаяс равенствоысь петӧ:

KA = KB = BL = LC = MC = MD =..., либӧ KL = LM = MN = ..., а сідзжӧ ∠K = ∠L = ∠M = ...

Та ногӧн описаннӧй KLMNPQ унапельӧсалӧн бокъясыс да пельӧсъясыс ӧтыдждаӧсь; сідзкӧ сійӧ — правильнӧй.

2. Правильнӧй вписаннӧй да описаннӧй унапельӧсаӧс вӧчӧм пӧрӧ кытшвизьӧс ӧтмында юкӧнъясӧ юкӧмӧ.

3. Теорема. Быд правильнӧй унапельӧсаӧ позьӧ впишитны кытшвизь да 2) йывъяс пырыс нуӧдны описаннӧй кытшвизь.

Сетӧма: ABCDEF — правильнӧй унапельӧса (267 серпас).

∠A = ∠B = ∠C = ... да AB = BC = CD = ...

_________________________________

Колӧ докажитны: 1) правильнӧй унапельӧсаӧ позьӧ впишитны кытшвизь,

2) йывъяс пырыс позьӧ нуӧдны описаннӧй кытшвизь.

Докажитӧм. 1) Медым унапельӧсаӧ впишитны кытшвизьӧс, колӧ тӧдны радиусыслысь кузьтасӧ да шӧрчутыслысь положенньӧсӧ. Вписаннӧй кытшвизьлӧн шӧрчут — унапельӧсаса став бокъяссянь ӧтылнаӧ ылысмӧдӧм чут. AB да BC бокъяссянь ӧтылнаӧ ылысмӧдӧм чутъяс куйлӧны ∠B биссектриса вылын; BC да CD бокъяссянь ӧтылнаӧ ылысмӧдӧм чутъяс куйлӧны ∠C биссектриса вылын, сідзкӧ, кыкнан биссектрисалӧн вомӧнасянін O чут ӧтылнаын AB, BC да CD бокъяссянь.

Докажитам, мый O чутӧс сідзжӧ ӧтылнаӧ ылысмӧдӧма унапельӧсаса CD да DE бокъяссянь, сідзкӧ сійӧ куйлӧ ∠D биссектриса вылын. Та могысь O чутӧс ӧтлаалам D йывкӧд да видзӧдлам ∆COD да ∆BOC. Сы вӧсна, мый налӧн OC бок — ӧтувъя, BC = CD да ∠OCB = ∠OCD, найӧ ӧтыдждаӧсь, мый вӧсна ∠OBC = ∠ODC, но ∠OBC = ∠B/2, сідзкӧ и ∠ODC = ∠B/2; сы вӧсна, мый ∠D = ∠B кыдзи правильнӧй унапельӧсалӧн пельӧсъяс, то ∠ODC = ∠D/2, сідзкӧ и OD лоӧ D пельӧслӧн биссектриса.

Тадз жӧ докажитӧны, мый OE, OF, OA — унапельӧсаса пельӧсъяслӧн биссектрисаяс, а тайӧ лоӧ, мый унапельӧсаса быд пельӧслӧн биссектрисаяс вомӧнасянін O чут став боксянь ӧтылнаын, сідзкӧ сійӧ вписаннӧй кытшвизьлӧн шӧрчут. OK = OL = OM = r, корсян кытшвизь r радиуслы.

2) BOC, COD... куимпельӧсаяс равенствоысь петӧ, мый OB = OC = ...; тайӧ лоӧ, мый O чутыс унапельӧсаса став йывсянь ӧтылнаын да лоӧ R = OB = OC... радиуса описаннӧй кытшвизьлӧн шӧрчут.

Правильнӧй унапельӧсаын описаннӧй да вписаннӧй кытшвизьяслӧн шӧрчутъяс ӧти чутынӧсь. Налӧн ӧтувъя шӧрчутыс шусьӧ правильнӧй унапельӧсаса шӧрчутӧн. O чутсянь правильнӧй унапельӧсаса бокъясӧдз OK, OL... расстоянньӧ шусьӧ апофемаӧн. Унапельӧсалӧн апофема ӧттшӧтш лоӧ вписаннӧй кытшвизьса радиусӧн.

3 §. Ӧтинима правильнӧй унапельӧсаяслӧн свойствояс.

1. Правильнӧй ӧтинима унапельӧсаяс подобнӧйӧсь, сы вӧсна, мый налӧн пельӧсъясыс ӧтыдждаӧсь, а бокъясыс пропорциональнӧйӧсь.

2. Теорема. Ӧтинима правильнӧй унапельӧсаяслӧн бокъяс относитчӧны кыдз описаннӧй либӧ вписаннӧй кытшвизьяслӧн радиусъяс.

Сетӧма: n — унапельӧсалӧн бок лыд (268-ӧд серпас);

AB да A₁B₁ — унапельӧсаяслӧн бокъяс;

OA да OB, ..., OA₁ да OB₁, ... — описаннӧй кытшвизьяслӧн радиусъяс;

OM да O₁M₁ — вписаннӧй кытшвизьяслӧн радиусъяс либӧ апофемаяс.

______________________________

Колӧ докажитны: AB/A₁B₁ = OA/O₁A₁ = OM/O₁M₁.

Докажитӧм. Кык ӧткузя бока A₁O₁B₁ да AOB куимпельӧсаясын ∠O₁ = ∠O сы вӧсна, мый на пиысь быд пельӧс 4d/n ыджда; сідзкӧ тайӧ куимпельӧсаяс подобнӧйӧсь, ∆AOB ∼ ∆A₁O₁B₁, мый вӧсна:

AB/A₁B₁ = OA/O₁A₁ = OM/O₁M₁,

правильнӧй ӧтинима унапельӧсаяслӧн бокъяс пропорциональнӧйӧсь описаннӧй кытшвизьяс радиусъяслы да апофемаяслы.

3. Следствие. Правильнӧй ӧтинима унапельӧсаяслӧн периметръяс относитчӧны, кыдз описаннӧй кытшвизьяслӧн радиусъяс либӧ апофемаяс.

Правильнӧй ӧтинима ABCDEF да A₁B₁C₁D₁E₁F₁ унапельӧсаяс подобнӧйӧсь, сідзкӧ налӧн сходственнӧй бокъясыс сідзжӧ пропорциональнӧйӧсь:

AB/A₁B₁ = BC/B₁C₁ = CD/C₁D₁ = ...,

но

(AB + BC + CD + ...)/(A₁B₁ + B₁C₁ + C₁D₁ + ...) = AB/A₁B₁,

либӧ P/P₁ = AB/A₁B₁, а сы вӧсна, мый AB/A₁B₁ = AO/A₁O₁ = OM/O₁M₁, то

P/P₁ = AO/A₁O₁ = OM/O₁M₁.

4 §. Правильнӧй унапельӧсалӧн площадь.

Теорема. Правильнӧй унапельӧсалӧн площадь равняйтчӧ периметрыслӧн апофема вылӧ произведенньӧ джынлы.

Сетӧма: a_n — правильнӧй n-пельӧсалӧн бок;

n — бокъясыслӧн лыд; OM = h — апофема;

p_n — сылӧн периметр (268-ӧд серпас).

_____________________________

Колӧ докажитны: n-пельӧсалӧн площадьыс S_n = ½p_n∙h.

Докажитӧм. Правильнӧй n-пельӧсалысь йывъяссӧ шӧрчутыскӧд ӧтлаалӧм мысти лоӧны n мында куимпельӧсаяс; найӧ — кык ӧткузя бокаӧсь да ӧтыдждаӧсь; на пиысь быд ӧтилӧн площадь S∆ = ½a_nh, кӧн h — куимпельӧсалӧн судта да ӧттшӧтш унапельӧсалӧн апофема; татысь быдса унапельӧсалӧн площадь:

S_n = n∙S∆ = ½na_nh;

но a_n∙n = p_n, та вӧсна S_n = ½p_n∙h.

Следствийӧяс. 1. Правильнӧй вписаннӧй унапельӧсалӧн площадь равняйтчӧ периметрыслӧн апофема вылӧ произведенньӧ джынлы (269 серп.):

S_n = ½p_nh.

2. Правильнӧй описаннӧй унапельӧсалӧн площадь равняйтчӧ периметрыс да кытшвизьса радиус произведенньӧ джынлы (269 серп.):

S_n = ½p_n∙h = ½p_n∙r.

3. Правильнӧй ӧтинима унапельӧсаяслӧн площадьяс относитчӧны кыдз бокъясыслӧн квадратъяс либӧ описаннӧй да вписаннӧй кытшвизьясса радиусъяслӧн квадратъяс (268 серп.).

ABCDEF да A₁B₁C₁D₁E₁F₁ — правильнӧй ӧтинима унапельӧсаяс; AO да A₁O₁ — налӧн радиусъясыс; OM да O₁M₁ — налӧн апофемаясыс; S да S₁ — налӧн площадьясыс.

Правильнӧй ӧтинима унапельӧсаяс подобнӧйӧсь, та вӧсна налӧн площадьясыс относитчӧны кыдз бокъясыслӧн квадратъяс:

S₁/S = A₁B₁²/AB². (1)

Правильнӧй ӧтинима унапельӧсаяслӧн бокъяс относитчӧны кыдз вписаннӧй либӧ описаннӧй кытшвизьяслӧн радиусъяс:

A₁B₁/AB = O₁A₁/OA = O₁M₁/OM. (2)

(1) да (2) равенствоясӧс ӧтластитӧмысь петӧ, мый

S₁/S = A₁B₁²/AB² = O₁A₁²/OA² = O₁M₁²/OM².

5 §. Кытшвизьӧ вписаннӧй квадрат. Сійӧс вӧчӧм да сылысь боксӧ радиус пыр петкӧдлӧм.

Задача. R радиуса кытшвизьӧ впишитны квадрат да сылысь a₄ боксӧ петкӧдлыны радиус пыр.

1) Построенньӧ. Кытшвизьын нуӧдам мӧда-мӧдлы перпендикулярнӧя кык диаметр — AC да BD (270 серпас); кытшвизьыс юксяс нёль ӧтыджда юкӧнӧ. Диаметръяслысь помъяссӧ ӧтлаалам водзысь-водзӧ да лоӧ правильнӧй вписаннӧй нёльпельӧса, мӧд ног кӧ, — квадрат: сы вӧсна, мый сылӧн бокъясыс ӧтыдждаӧсь кыдз ӧтыджда дугаясӧс стягивайтан хордаяс, а сылӧн быд пельӧс веськыд кыдз диаметр вылӧ пыксян пельӧс.

2) Арталӧм. Веськыдпельӧса AOB куимпельӧсаысь сюрӧ:

AB² = AO² + BO², либӧ AB² = 2R², кытысь .

Правильнӧй вписаннӧй нёльпельӧсалӧн бокыс: .

6 §. Вписаннӧй правильнӧй квайтпельӧса. Сійӧс вӧчӧм да боксӧ радиус пыр петкӧдлӧм.

Задача. R радиуса кытшвизьӧ впишитны правильнӧй квайтпельӧса да сылысь a₆ боксӧ мыччӧдны радиус пыр.

Решитӧм. Анализ. Мед AB лоӧ (271 серпас) правильнӧй вписаннӧй квайтпельӧсалӧн бок, сэк ∠AOB = 360°/6 = 60°. ∆AOB — кык ӧткузя бока, OA = OB = R да ∠A = ∠B; тайӧ кыкнан пельӧсыс 60° ыдждаӧсь. ∆AOB — ӧтыдждапельӧса, сідзкӧ, ӧткузя бокъяса; та вӧсна AB = AO = BO = R.

Правильнӧй вписаннӧй квайтпельӧсалӧн бок: a₆ = R.

Построенньӧ. Паськӧдам циркуль кокъяссӧ кытшвидз радиус ыдждаӧдз да вундалам кытшвизьсӧ квайт ӧтыджда дугаӧ; быд дугалысь помъяссӧ ӧтлаалам хордаясӧн да лоӧ правильнӧй квайтпельӧса.

7 §. Правильнӧй вписаннӧй куимпельӧса. Сійӧс вӧчӧм да боксӧ радиус пыр петкӧдлӧм.

Задача. R радиуса кытшвизьӧ впишитны правильнӧй куимпельӧсаӧс да сылысь a₃ боксӧ петкӧдлыны радиус пыр.

1) Построенньӧ. Юкам кытшвизьӧс квайт ӧтыджда юкӧнӧ. Быд ӧти чут вомӧн вуджӧмӧн юкан чутъяссӧ ӧтлаалам хордаясӧн да лоӧ корсян правильнӧй ABC куимпельӧса (272 серпас), кодлӧн AB = BC = CA кыдз ӧтыджда дугаясӧс стягивайтан хордаяс.

2) Боксӧ арталӧм. AD диаметр нуӧдӧм бӧрын да D чут B чуткӧд ӧтлаалӧм бӧрын лоӧ B йыв бердын веськыдпельӧса ABD куимпельӧса. Тайӧ куимпельӧсаысь лоӧ:

AB² = AD² − DB²; AD = 2R да DB = R,

та вӧсна

AB² = a₃² = 4R² − R² = 3R²,

кытысь

8 §. Правильнӧй куимпельӧсалысь судтасӧ да площадьсӧ да описаннӧй да вписаннӧй кытшвизьлысь радиусъяссӧ тайӧ куимпельӧсаса бок пыр петкӧдлӧм.

Сетӧма правильнӧй ∆ABC (273 серпас). Сылӧн бокыс AB = a; OM = r — вписаннӧй кытшвизьлӧн радиус; OA = OC = R — описаннӧй кытшвизьлӧн радиус; CM = h — судта; S — сылӧн площадьыс.

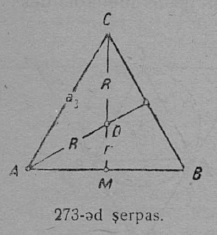
1) R арталӧм. Бок

татысь петӧ, мый

2) r арталӧм. Веськыдпельӧса AOM куимпельӧсаын гипотенуза AO = R лоӧ ABC куимпельӧсаса ∠A-лӧн биссектриса, сідзкӧ, ∠OAM = 30°, та вӧсна катет OM = r, кыдз 30° пельӧс водзын куйлысь, гипотенуза джын ыджда: r = R/2. Та ногӧн

R = 2r.

3) h арталӧм. Судта h = CM = CO + OM, но CO = R = 2r да OM = r = R/2; та вӧсна:

1) h = R + R/2 = 1,5R; 2) h = 2r + r = 3r;

3) h = 3r = 3∙a/6 = a/2.

4) S арталӧм. Площадь

S = ½ah = ½a∙a/2 = a² /4 кв. единица.

9 §. Описаннӧй квадратӧс да правильнӧй описаннӧй куимпельӧсаӧс вӧчӧм да налысь бокъяссӧ радиус пыр петкӧдлӧм.

Задача 1. Вӧчны описаннӧй квадрат да сылысь b₄ боксӧ мыччӧдны вписаннӧй кытшвизьса r радиус пыр.

Решитӧм. r радиуса кытшвизьӧ впишитам квадрат (274 серпас). Сійӧ йывъяс пырыс нуӧдалам касательнӧйясӧс мӧда-мӧдыскӧд вомӧнасьтӧдз; лоӧ описаннӧй KLMN квадрат. Сылӧн KL бокыс = b₄ лоӧ DB диаметр ыджда, та вӧсна:

b₄ = 2r.

Задача 2. Вӧчны правильнӧй описаннӧй куимпельӧсаӧс да сылысь b₃ боксӧ мыччӧдны вписаннӧй кытшвизь r радиус пыр.

Решитӧм. r радиуса кытшвизьӧ впишитам правильнӧй куимпельӧсаӧс (275 серпас). Сійӧ йывъяс пыр нуӧдалам касательнӧйясӧс мӧда-мӧдыскӧд вомӧнасьтӧдз; лоӧ правильнӧй описаннӧй KLM куимпельӧса. KLM куимпельӧсаын A да B касанньӧ чутъяс — KM да LM бокъяслӧн шӧръяс, сы вӧсна, мый KA = AM да LB = BM; татысь петӧ, мый AB = a₃ — KLM куимпельӧсалӧн шӧр визь. Но AB = KL/2, либӧ a₃ = b₃/2, татысь b₃ = 2a₃ —

правильнӧй описаннӧй куимпельӧсалӧн бокыс кык пӧв ыджыдджык сійӧ жӧ кытшвизьӧ вписаннӧй куимпельӧсалӧн бокысь:

10 §. Правильнӧй описаннӧй унапельӧсалысь боксӧ правильнӧй ӧтинима вписаннӧй унапельӧсаса бок пыр да радиус пыр петкӧдлӧм.

1. Задача. Правильнӧй вписаннӧй унапельӧсаса бок пыр да радиус пыр петкӧдлыны ӧтинима правильнӧй описаннӧй унапельӧсалысь боксӧ.

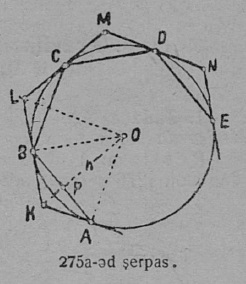
Решитӧм. ABCD... да KLMN... унапельӧсаяс (275a-ӧд серпас) — правильнӧйӧсь да ӧтинимаӧсь, сідзкӧ, найӧ подобнӧйӧсь. Бок KL = b_n, бок AB = a_n. Унапельӧсаяс подобийӧысь петӧ, мый

b_n/a_n = R/h, кытысь b_n = a_nR/h. (1)

Веськыдпельӧса OPB куимпельӧсалысь, кодлӧн катет PB = a_n/2, определитам h:

h-лы сюрӧм (2) выраженньӧсӧ (1) равенствоӧ пуктам да лоӧ:

2. Тайӧ формула кузя вермам тӧдмавны правильнӧй вписаннӧй унапельӧсаса a_n бок серти да R радиус серти ӧтинима описаннӧй правильнӧй унапельӧсалысь b_n боксӧ.

3. Артмӧм формулалысь кӧ кыкнан пайсӧ лэптыны квадратӧ да определитны a_n, лоӧ:

Тайӧ формула кузя вермам тӧдмавны правильнӧй описаннӧй унапельӧсаса b_n бок серти да R радиус серти ӧтинима вписаннӧй правильнӧй унапельӧсалысь a_n боксӧ.

4. Задача. Правильнӧй описаннӧй квайтпельӧсалысь b₆ боксӧ петкӧдлыны вписаннӧй кытшвизьса R радиус пыр.

Решитӧм. Задача решитӧм вылӧ босьтам формула:

Унапельӧсаса бокъяслӧн n лыд задача условийӧ серти — 6; сідзкӧ, a_n = a₆ = R; та вӧсна:

11 §. Правильнӧй вписаннӧй унапельӧсалысь бокъяс лыдсӧ кыкпӧлалӧм.

1. Задача. Правильнӧй вписаннӧй унапельӧсалысь кыкпӧлавны бокъяс лыдсӧ да сылысь a_2n боксӧ петкӧдлыны a_n да R пыр.

Решитӧм. 1) Мед AB = a_n лоӧ правильнӧй вписаннӧй n-пельӧсалӧн бок (276 серпас). Медым вӧчны сетӧм унапельӧсаысь кык мында бокъяса вписаннӧй унапельӧсаӧс, колӧ кытшвизьсӧ юкны 2n ӧтыджда юкӧнӧ. AB боклы соответствуйтысь AB дугаӧс юкам шӧри; сэк ‿AC = ‿CB да AC хорда лоӧ 2n бока вписаннӧй унапельӧсалӧн бокӧн.

2) AC = a_2n арталӧм вылӧ видзӧдлам ёсьпельӧса ∆AOC да гижам, ыджыд-ӧ тайӧ боклӧн квадрат:

AC² = AO² + OC² − 2OC∙OD, либӧ:

a_2n² = R² + R² − 2R∙OD = 2R² − 2R∙OD. (1)

Веськыдпельӧса ∆AOD-ысь:

(1) равенствоысь OD-ӧс вежам (2) равенствоын сылы артмӧм значенньӧӧн да лоӧ:

кытысь:

Тайӧ формула — правильнӧй вписаннӧй n-пельӧсалысь бокъяс лыдсӧ кыкпӧлалан формула. Тайӧ формула кузя вермам тӧдмавны правильнӧй вписаннӧй n-пельӧсаса a_n бок серти да R радиус серти правильнӧй вписаннӧй 2n-пельӧсалысь a_2n боксӧ.

2. Пример. Правильнӧй вписаннӧй даскыкпельӧсалысь боксӧ петкӧдлыны R пыр.

Решитӧм.

сы вӧсна, мый a₆ = R,

либӧ, сы вӧсна мый

Юасянъяс да упражненньӧяс.

1. R радиуса кругӧ впишитны правильнӧй кӧкъямыспельӧсаӧс да сылысь боксӧ мыччӧдны радиус пыр.

2. Правильнӧй вписаннӧй куимпельӧсаса, нёльпельӧсаса, кӧкъямыспельӧсаса сетӧм a бок серти тӧдмавны круглысь радиус.

3. R радиуса кругӧ впишитӧма правильнӧй кӧкъямыспельӧсаӧс, даскыкпельӧсаӧс. Определитны диагональясыслысь кузьтаяссӧ.

4. Правильнӧй описаннӧй квайтпельӧсалӧн бок b ыджда. Определитны круглысь радиус.

5. Правильнӧй кӧкъямыспельӧсалысь сетӧма боксӧ — a. Вӧчны сійӧс.

6. Круглӧн радиус R ыджда. Тӧдам, мый . Определитны правильнӧй вписаннӧй витпельӧсалысь боксӧ.

7. h апофема серти вӧчны: 1) правильнӧй куимпельӧсаӧс, 2) квадратӧс, 3) правильнӧй квайтпельӧсаӧс.

XXI. КЫТШВИЗЬЛӦН КУЗЬТА ДА КРУГЛӦН ПЛОЩАДЬ.

1 §. Кытшвизьлысь кузьтасӧ правильнӧй вписаннӧй да описаннӧй унапельӧсаяс периметръяскӧд ӧтластитӧм.

1. Сы вӧсна, мый линейнӧй мераӧс, кыдз веськыд визьлысь вундӧгӧс, он вермы ӧтлаавны нюкыля визькӧд, кытшвизьлысь кузьтасӧ сы вылӧ линейнӧй мераӧс пукталӧмӧн непосредственнӧя муртавны оз позь; та вӧсна кытшвизьлысь кузьтасӧ определитӧны косвеннӧй приёмӧн: правильнӧй вписаннӧй да описаннӧй унапельӧсаяслысь периметръяссӧ мурталан способӧн.

Кытшвизь кузьталы формула выводитан теоремаясӧс видлалӧм водзвылын тӧдмалам, кутшӧм эм зависимосьт разнӧй визьяс кузьта костын, кодъяслӧн помъясыс лоӧны кык чут A да B.

Мед сетӧма кык чегласьӧм визь AEDCB да AFGB, на пиысь AEDCB визьыс — объемлющӧй да AFGB-ыс — объемлемӧй чегласьӧм визь, кодъяслӧн помъясыс лоӧны кык чут A да B.

Петкӧдлам, мый AFGB объемлемӧй чегласьӧм визь дженьыдджык любӧй AEDCB объемлющӧй чегласьӧм визьысь, кодъяслӧн A да B помъясыс ӧтлаасьӧны.

Збыльысь ӧд, AFGB чегласьӧм визьлысь FG боксӧ кӧ кыкнанла дорӧ нюжӧдан, кытчӧдз оз вомӧнасьны AEDCB чегласьӧм визькӧд (277 серп.), сэк лоӧ:

AF < AK + KF; KF + FG + GL < KE + ED + DC + CL; GB < GL + LB.

Тайӧ неравенствояссӧ членӧн-членӧн содталӧмӧн миян лоас:

AF + KF + FG + GL + GB < AK + KF + KE + ED + DC + CL + GL + LB,

либӧ неравенствоса кыкнан юкӧнсьыс KF да GL чинтӧм бӧрын лоӧ

AF + FG + GB < AE + ED + DC + CB,

либӧ мӧд ног кӧ шуны, выпуклӧй объемлемӧй чегласьӧм визь дженьыдджык быд объемлющӧй чегласьӧм визьысь, кодлӧн помъясыс ӧтлаасьӧны объемлемӧй визь помъяскӧд.

Висьталӧмтор лоӧ веськыдӧн и сійӧ случайын, кор объемлющӧй либӧ объемлемӧй визьяс лоӧны кытшвизьса дугаясӧн, тадзсӧ сы вӧсна, мый кытшвизьса дугаӧс позьӧ видлавны кыдзи зэв дженьыдик зэв уна звеноысь тэчсьӧм чегласьӧм визьӧс.

Пример, DC₁F дуга (278 серпас, 172 листбок) дженьыдджык DCF чегласьӧм визьысь, коді тэчсьӧма CD да CF кык касательнӧйысь; дзик жӧ сідзи DC₁F дуга дженьыдджык DQPF чегласьӧм визьысь, мӧд ног кӧ, ‿DC + ‿CF < DQ + QP + PF.

2. Теорема. Правильнӧй вписаннӧй унапельӧсалӧн периметр кытшвизь кузьтаысь ичӧтджык да матысмӧ сы дінӧ, кымын кутам унапельӧсалысь бокъяс лыдсӧ кыкпӧлавны.

Сетӧма: p_n — n-пельӧсалӧн периметр;

C — кытшвизьлӧн кузьтаыс (277a-ӧд серпас).

________________________________________

Колӧ докажитны: p_n < C да бокъяслысь n лыдсӧ кыкпӧлалігӧн матысмӧ C дінӧ.

Докажитӧм. AB — правильнӧй вписаннӧй ABC куимпельӧсалӧн бок; сылӧн периметр p₃ = 3AB. AB, BC да CA дугаясӧс юкам шӧри да юкан D, E да F чутъясӧс тайӧ дугаясыс помъяскӧд ӧтлаалам; лоӧ правильнӧй вписаннӧй квайтпельӧса, кодлӧн периметр p₆ = 6AD правильнӧй вписаннӧй куимпельӧсаса периметрысь ыджыдджык. Тайӧ мый тадз, петӧ вот кыдзи: ADB куимпельӧсаысь лоӧ: AD + DB > AB, но AD = DB, та вӧсна 2AD > AB; тайӧ неравенстволысь кыкнан пайсӧ 3 вылӧ ӧктӧм мысти лоӧ: 6AD > 3AB, либӧ p₆ > p₃. AD, DB, BE, EC... дугаясӧс шӧри юкӧм бӧрын да юкан K, L, M, N... чутъяссӧ тайӧ дугаяс помъясыскӧд ӧтлаалӧм бӧрын лоӧ правильнӧй вписаннӧй даскыкпельӧса, кодлӧн периметрыс p₁₂ > p₆. Тайӧ сы вӧсна, мый ADK куимпельӧсаысь петӧ: AK + KD > AD, но KD = AK, та вӧсна 2AK > AD; неравенстволысь кыкнан пайсӧ 6 вылӧ ӧктӧм бӧрын лоӧ, мый 12AK > 6AD, либӧ p₁₂ > p₆.

Кутам кӧ водзӧ тадз жӧ быд выльӧн артмӧм унапельӧсалысь бокъяс лыдсӧ кыкпӧлавны, аддзам, мый правильнӧй вписаннӧй унапельӧсалӧн периметр сымын ыджыд, мый уна сылӧн бок.

Лоӧ: p₆ > p₃; p₁₂ > p₆... ӧтувйӧн p_2n > p_n, кӧн p_n — правильнӧй вписаннӧй n бока унапельӧсалӧн периметр, а p_2n лоӧ 2n бока унапельӧсалӧн периметр.

Та ногӧн, кымын унаысь кыкпӧлалам правильнӧй вписаннӧй унапельӧсалысь бокъяс лыдсӧ, сымын содӧ сылӧн периметрыс да матысмӧ кытшвизь кузьта дінӧ, но век лоӧ сыысь ичӧтджык. Тайӧ сы вӧсна, мый правильнӧй вписаннӧй унапельӧсалӧн бокъяс кыдз хордаяс ичӧтджыкӧсь наӧн стягивайтан дугаяссьыс; та вӧсна унапельӧсаса став бокъяслӧн сумма кытшвизьса став дугаяс суммаысь ичӧтджык, татысь петӧ, мый правильнӧй вписаннӧй унапельӧсалӧн, кӧть медым мыйта бока сійӧ эз вӧв, периметрыс век лоӧ кытшвизь кузьтаысь ичӧтджык.

Кытшвизьлысь кузьтасӧ пасъям C пыр, вӧчӧм вывод гижсяс тадз: p_n < C.

Правильнӧй вписаннӧй унапельӧсалысь бокъяс лыдсӧ помтӧм унаысь кыкпӧлалігӧн сылӧн периметрыс кытшвизь кузьта дінӧ сэтшӧма матысмас, мый кытшвизь кузьта да периметр костын C − p_n разносьт лоӧ помтӧм ичӧт.

3. Теорема. Правильнӧй описаннӧй унапельӧсалӧн периметр кытшвизь кузьтаысь ыджыдджык да матысмӧ сы дінӧ, кор унапельӧсалысь бокъяс лыдсӧ кутам водзысь-водзӧ кыкпӧлавны.

Сетӧма: P_n — унапельӧсалӧн периметр; C — кытшвизьлӧн кузьта (278-ӧд серпас).

_____________________________________

Колӧ докажитны: P_n > C да бокъяслысь n лыдсӧ кыкпӧлалігӧн матысмӧ C дінӧ.

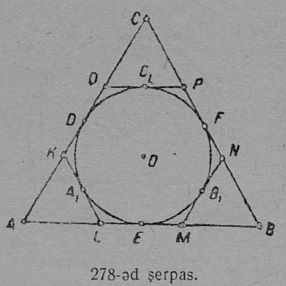
Докажитӧм. AB — правильнӧй описаннӧй ABC куимпельӧсалӧн бок; сылӧн периметр P₃ = 3AB. Описаннӧй ABC куимпельӧсаса бокъяслӧн кытшвизьӧ касанньӧ D, E да F чутъяс костса дугаясӧс юкам шӧри да юкан A₁, B₁ да C₁ чутъяс пыр нуӧдам касательнӧйясӧс; лоӧ правильнӧй описаннӧй KLMNPQ квайтпельӧса, кодлӧн периметр P₆ = 6KL P₃-ысь ичӧтджык; P₆ < P₃. Тайӧ тадз сы вӧсна, мый AKL, BMN, CQP куимпельӧсаясысь петӧ: KL < AK + AL; MN < BM + BN; PQ < CQ + CP, а тайӧ лоӧ, мый ABC куимпельӧсаса бокъясысь шыблассян AK да AL, BM да BN, CQ да CP вундӧгъяслӧн суммаяс вежсьӧны ичӧтджык KL, MN да PQ вундӧгъясӧн, та вӧсна P₆ < P₃. Правильнӧй описаннӧй квайтпельӧсалысь бокъяс лыдсӧ та ногӧн жӧ кыкпӧлалӧм бӧрын артмас правильнӧй описаннӧй даскыкпельӧса, кодлӧн периметр лоӧ описаннӧй квайтпельӧса периметрысь ичӧтджык: P₁₂ < P₆ да с. в.; вообще, P_2n < P_n.

Та ногӧн, кымын унаысь кыкпӧлалам правильнӧй описаннӧй унапельӧсалысь бокъяс лыдсӧ, сымын чинӧ сылӧн периметрыс да матысмӧ кытшвизь кузьта дінӧ, но век лоӧ сыысь ыджыдджык.

Тайӧ вывод гижсяс тадз: P_n > C.

Правильнӧй описаннӧй унапельӧсалысь бокъяс лыдсӧ помтӧм унаысь кыкпӧлалігӧн сылӧн периметрыс кытшвизь кузьта дінӧ сэтшӧма матысмас, мый периметр да кытшвизь кузьта костын P_n − C разносьт лоӧ помтӧм ичӧт.

4. Тайӧ кык бӧръя теоремалысь выводъяссӧ ӧтлаалӧмысь петӧ: p_n < C < P_n, мый лоӧ: кытшвизьлӧн кузьтаыс правильнӧй вписаннӧй унапельӧсаса периметрысь ыджыдджык, правильнӧй описаннӧй унапельӧсаса периметрысь ичӧтджык; та дырйи тайӧ унапельӧсаяслӧн периметръяс, кодъяс унапельӧсаяслысь бокъяс лыдсӧ кыкпӧлалігӧн вежсьӧны, водзысь-водзӧ матысмӧны кытшвизь кузьта дінӧ, коді век кольӧ вежсьытӧг.

2 §. Постояннӧй да переменнӧй величинаяс йылысь вежӧртас.

1. Правильнӧй вписаннӧй да описаннӧй унапельӧсаяслӧн периметръяс p_n да P_n, кор налысь бокъяссӧ кутам помтӧм унаысь кыкпӧлавны, вежласьӧны да водзысь-водзӧ матысмӧны кытшвизь кузьта дінӧ, кыдз быттьӧ стремитчӧны сыкӧд ӧтыдждаӧн лоны; та дырйи кытшвизьлӧн кузьта оз вежлась: век кольӧ ӧтыдждаӧн.

2. Величина, коді сетӧм задача условийӧяс серти босьталӧ различнӧй значенньӧяс, шусьӧ переменнӧй величинаӧн; сійӧ величина, кодлӧн сійӧ жӧ условийӧяс серти значенньӧыс оз вежлась, а кольӧ век ӧти, шусьӧ постояннӧй величинаӧн.

Переменнӧй величинаяс вылӧ примеръясӧн лоӧны вписаннӧй да описаннӧй унапельӧсаяслӧн помтӧм унаысь бокъяс лыдсӧ кыкпӧлалӧм дырйи p_n да P_n периметръяс, а кытшвизьлӧн C кузьта — постояннӧй величина.

3. Постояннӧй да переменнӧй величинаяс вылӧ ӧти сійӧ жӧ задачаса условийӧяс серти примеръяс:

1) Сетӧма ABC куимпельӧса (279 серп.). Кор кутам сылысь C йывсӧ местанас вежлавны AB подувтаслы параллельнӧй веськыд визь кузя, а AB подувтассӧ эновтам вӧрзьытӧг, переменнӧй величинаясӧн лоӧны: 1) боквывса бокъяслӧн кузьтаясыс; 2) периметрыс, 3) быд пельӧслӧн ыдждаыс; постояннӧй величинаясӧн — 1) подувтасыс, 2) пельӧсъясыслӧн суммаыс = 2d, 3) судтаыс да 4) площадьыс.

2) Сетӧма R радиуса кытшвизь (280 серп.); AB = a_n — правильнӧй вписаннӧй n-пельӧсалӧн бок; OM ⊥ AB вундӧг — апофема; пасъям сійӧс h_n-ӧн.

n-пельӧсалысь бокъяс лыдсӧ кыкпӧлалӧм бӧрын лоӧ AC = a_2n да ON ⊥ AC вундӧг — апофема, кодӧс пасъям h_2n-ӧн.

Веськыдпельӧса OMK куимпельӧсаысь аддзам, мый OK > OM, но OK ON-лӧн сӧмын юкӧн, та вӧсна ON нӧшта нин ыджыд OM-ысь. Та ногӧн, ON > OM либӧ h_2n > h_n; тайӧ петкӧдлӧ, мый кымын унаысь куимпельӧсалысь^унапельӧсалысь?/^ бокъяссӧ кыкпӧлалам, сымын апофема содӧ да матысмӧ R радиус кузьта дінӧ, но некор оз ло сы кузьта: век кольӧ сыысь ичӧтджыкӧн.

Та ногӧн унапельӧсалысь бокъяс лыдсӧ помтӧм унаысь кыкпӧлалігӧн h_n апофема — переменнӧй величина; кытшвизьлӧн радиус — постояннӧй величина да радиус кузьта да апофема кузьта костын R − h_n разносьт лоӧ век ичӧтджык да ичӧтджык да, кор унапельӧса лоӧ помтӧм уна бока, лоӧ бырана ичӧтӧн.

3 §. Предел йылысь вежӧртас. Кытшвизь кыдз вписаннӧй да описаннӧй унапельӧсаясса периметръяслӧн предел.

1. Правильнӧй вписаннӧй унапельӧсалӧн периметр помтӧм унаысь бокъяс лыдсӧ кыкпӧлалігӧн содӧ да матысмӧ кытшвизь кузьта дорӧ; та дырйи сетӧм кытшвизь кузьта да правильнӧй вписаннӧй унапельӧсалӧн периметр костын разносьтыс лоӧ сымын ичӧт, кымын уна лоӧ вписаннӧй унапельӧсалӧн бокыс, а бокъяссӧ помтӧг ыдждӧдігӧн стремитчӧ нульӧ.

2. Правильнӧй описаннӧй унапельӧсалӧн периметр помтӧм унаысь бокъяс лыдсӧ кыкпӧлалігӧн чинӧ да кузьтанас сідзжӧ стремитчӧ лоны кытшвизь кузьта ыдждаӧн; та дырйи сетӧм кытшвизь кузьта да правильнӧй описаннӧй унапельӧсалӧн периметр костын разносьтыс сымын ичӧт, кымын уна лоӧ описаннӧй унапельӧсалӧн бок.

3. Унапельӧсалысь бокъяс лыдсӧ помтӧм унаысь кыкпӧлалігӧн кыдз вписаннӧйлӧн периметр, коді водзысь-водзӧ содӧ, сідз и описаннӧйлӧн периметр, коді водзысь-водзӧ чинӧ, оз вермыны лоны кытшвизь кузьтакӧд ӧтыдждаӧн. Кытшвизь лоӧ налӧн пределӧн.

4. Постояннӧй величина, код дінӧ переменнӧй величина матысмӧ сідз, мый на костса разносьтсӧ абсолютнӧй величинанас позьӧ вӧчны кутшӧм колӧ водзвыв сетӧм величинаысь ичӧтджыкӧн да та бӧрын кольӧ сыысь ичӧтджыкӧн, шусьӧ переменнӧй величина пределӧн.

Та ногӧн, кытшвизь лоӧ правильнӧй вписаннӧй да описаннӧй унапельӧсаяслысь бокъяссӧ кыкпӧлалігӧн найӧ периметръяс пределӧн.

Тайӧ положенньӧыс гижсьӧ тадз: унапельӧсаса бокъяс лыд помтӧма содігӧн предел p_n = C либӧ P_n = C; либӧ lim p_n = C; lim P_n = C, кӧн lim мыччӧдлӧ предел; lim лоӧ латинскӧй кыв “limes” дженьыда пасйӧм (кыв “limes” — предел).

Унапельӧсаса бокъяс лыдӧс помтӧма кыкпӧлалігӧн C да p_n да P_n да C костын разносьт водзысь-водзӧ чинӧмӧн вермӧ лоны бырана ичӧтӧн; та серти кытшвизь кузьта пыдди приближённӧя босьтӧны зэв уна бока вписаннӧй либӧ описаннӧй унапельӧсалысь периметр.

5. Переменнӧй величина, коді век чинӧ да вермӧ лоны да водзӧ кольны кутшӧм колӧ водзвыв сетӧм величинаысь ичӧтджыкӧн, шусьӧ помтӧм ичӧт величинаӧн.

Шуӧны, мый помтӧм ичӧт величина вежласигас стремитчӧ нуль дінӧ, мый нуль — сылӧн предел. Помтӧм ичӧт величинаяс вылӧ примеръясӧн вермӧны лоны: описаннӧй кытшвизьлӧн радиус да правильнӧй вписаннӧй унапельӧсалӧн бокъяс лыдсӧ помтӧм унаысь кыкпӧлалігӧн апофема костын разносьт; кытшвизь кузьта да вписаннӧй унапельӧсалӧн периметр костын разносьт; описаннӧй унапельӧсалӧн периметр да вписаннӧй кытшвизь кузьта костын разносьт, кор унапельӧсаяслысь бокъяс лыдсӧ помтӧм унаысь кыкпӧлалӧны.

Гижӧд:

R − h_n помтӧм ичӧт ыджда

C − p_n помтӧм ичӧт ыджда

P_n − C помтӧм ичӧт ыджда

правильнӧй унапельӧсалысь бокъяс лыдсӧ помтӧм унаысь кыкпӧлалігӧн.

4 §. Кытшвизьлысь кузьтасӧ арталӧм. π лыд.

1. Кытшвизьлысь кузьтасӧ линейнӧй мераӧн непосредственнӧя муртавны оз позь. Сылысь кузьтасӧ определитӧны кыдз предел, код дінӧ стремитчӧ правильнӧй вписаннӧй либӧ описаннӧй унапельӧсалӧн периметр, кор сылысь доръяс лыдсӧ помтӧм унаысь кыкпӧлалӧны.

2. Татысь петӧмӧн арталӧны зэв уна бока правильнӧй вписаннӧй либӧ описаннӧй унапельӧсалысь периметрсӧ да сюрӧм результатсӧ босьтӧны кытшвизь кузьта пыдди. Сетӧм кытшвизь радиус серти, правильнӧй вписаннӧй да описаннӧй унапельӧсаса боклысь кузьтасӧ арталӧм вылӧ пӧльзуйтчӧны формулаясӧн:

да

Правильнӧй вписаннӧй да описаннӧй унапельӧсаяслысь, кодъяслысь бокъяс лыдсӧ водзысь-водзӧ кыкпӧлалӧма, сетӧм кытшвизь радиус серти бокъясыслысь кузьтаяссӧ да сідзжӧ периметръяссӧ арталӧмъяслысь результатсӧ мыччӧдӧма табличаын. Описаннӧй да вписаннӧй ӧтинима правильнӧй унапельӧсаяслӧн периметръяс костысь разносьт арталӧма 0,00001-ӧдз точносьтӧн.

n — бокъяслӧн лыд	an — вписаннӧй унапельӧсалӧн бок	pn — вписаннӧй унапельӧсалӧн периметр	bn — описаннӧй унапельӧсалӧн бок	Pn — описаннӧй унапельӧсалӧн периметр	Pn − pn — периметръяс костын разносьт
6	1,0000000R	6,00000R	1,1547006R	6,92820R	0,92820R
12	0,5176381R	6,21166R	0,5358984R	6,43078R	0,21912R
24	0,2610524R	6,26526R	0,2633050R	6,31932R	0,05406R
48	0,1308063R	6,27870R	0,1310869R	6,29217R	0,01347R
96	0,0654382R	6,28206R	0,0654732R	6,28543R	0,00337R
192	0,0327235R	6,28290R	0,0327278R	6,28375R	0,00085R
384	0,0163623R	6,28311R	0,0163628R	6,28333R	0,00022R
768	0,0081812R	6,28317R	0,0081813R	6,28322R	0,00005R
1536	0,0040906R	6,28318R	0,0040906R	6,28319R	0,00001R

Табличаысь тыдалӧ, мый унапельӧсаяслысь бокъяс лыд кыкпӧлалӧм серти: 1) a_n чинӧ да p_n содӧ; 2) b_n чинӧ да P_n чинӧ; 3) a_n да b_n, p_n да P_n-лӧн лыда значенньӧясыс водзысь-водзӧ матысмӧны мӧда-мӧд дінас; 4) описаннӧй да вписаннӧй унапельӧсаяслӧн периметръяс костса P_n − p_n разносьт водзысь-водзӧ ичӧтмӧ.

Тадз и колӧ лоны, — кыкнан периметрыс вочасӧн матыстчӧны ӧти сійӧ жӧ предел дінӧ — кытшвизь кузьта дінӧ, стремитчӧны сыкӧд ӧтлаасьны, лоны кузьтананыс сыкӧд ӧтыдждаӧн.

Гӧгӧрвоана, мый ӧтинима правильнӧй описаннӧй да вписаннӧй 768 бока унапельӧсаяслӧн периметръяс костын кӧ разносьтыс 0,00005R гӧгӧр ыджда, сетӧм кытшвизь кузьта да вписаннӧй унапельӧсалӧн периметр костын разносьт либӧ описаннӧй унапельӧсалӧн периметр да сетӧм кытшвизь кузьта костын разносьт лоӧ 0,00005R дорысь ичӧтджык, та вӧсна кытшвизь кузьта пыдди позьӧ приближённӧ босьтны зэв уна бока правильнӧй описаннӧй либӧ вписаннӧй унапельӧсалысь периметр; кымын уна лоӧ бок лыдыс, сымын стӧчджык лоӧ матыстӧмыс.

Сідз, босьтам кӧ 1 м кузя радиуса кытшвизь, то P_n − p_n разносьт n = 768 дырйи матӧ лоӧ 0,00005 м = 0,005 см = 0,05 мм: сӧмын миллиметр ӧти кызьӧд юкӧн ыджда. Гӧгӧрвоана, мый 1 м кузя радиуса кытшвизьлӧн кузьта кутас торъявны вписаннӧй либӧ описаннӧй унапельӧсалӧн периметрысь нӧшта ичӧтджык величинаӧн.

Тадз, R радиуса кытшвизьлӧн C кузьта 0,0001 точносьтӧн 6,2832R гӧгӧр ыджда; C = 6,2832R.

Тайӧ выраженньӧын кӧ кытшвизьлысь R радиуссӧ вежам D диаметр джыннас, R пыдди кӧ пуктам D/2, лоӧ:

C = 6,2832R = 6,2832∙D/2 = 3,1416D.

Тайӧ формула петкӧдлӧ, мый кытшвизьлӧн C кузьта артмӧ диаметрсӧ 3,1416 лыд вылӧ ӧктӧмӧн.

3. C ≈ 3,1416D лоӧ справедливӧй любӧй диаметра кытшвизьлысь кузьта корсьӧм вылӧ. Формулаысь петӧ: C/D ≈ 3,1416. Тайӧ отношенньӧ петкӧдлӧ, мый кытшвизьлӧн кузьта ас диаметрсьыс 3,1416 пӧв ыджыдджык.

Кытшвизь C кузьталӧн D диаметрыс дорӧ отношенньӧыс — постояннӧй лыд, приблизительнӧ 3,1416 ыджда.

Тайӧ постояннӧй лыдсӧ пасйӧны греческӧй шыпасӧн π (лыддьыссьӧ “пи”); сідзкӧ, π ≈ 3,1416. Формулаӧ тайӧс пыртӧмӧн кытшвизь C кузьталӧн формула лоӧ татшӧм вида: C/D = π, либӧ C = πD, либӧ C = 2πR —

кытшвизьлӧн кузьтаыс ас диаметрсьыс π пӧв ыджыдджык, либӧ ас радиуссьыс 2π пӧв ыджыдджык.

4. π лыд — иррациональнӧй лыд, та вӧсна сійӧс оз позь мыччӧдны некутшӧм рациональнӧй дробӧн. Кор ми кытшвизь C кузьта пыдди босьтім 768 бока правильнӧй описаннӧй унапельӧсалысь периметрсӧ, миян лои π-лы матысмӧдӧм лыд 3,1416 избытокӧн да 0,0001 точносьтӧн.

Практическӧй уджъяс дырйи C кузьтаӧс арталігӧн тырмымӧн лоӧ босьтны π = 3,14 (0,01 точносьтӧн).

Задачаясӧс решитігӧн ковмывлӧ пӧльзуйтчыны π лыдлы мӧдара лыдӧн: 1/π дробӧн; 1/π = 0,318 (0,001 точносьтӧн), 0,01 точносьтӧн 1/π лоӧ 0,32 ыджда.

5. Уна сюрс во чӧж математикъяс корсисны туйяс артавны кытшвизьлысь кузьтасӧ. Важ вавилоняна да еврейяс кытшвизьлысь кузьта арталісны 3 диаметр ыдждаӧн. Архимед, зэв ыджыд важся математик, π лыдлы корсис 3⅐ лыд, та дырйи сійӧ пӧльзуйтчис сійӧ жӧ приёмӧн, кодӧс индӧма тайӧ книгаын. Птоломейлысь, индусъяслысь, сёрӧнджык арабъяслысь аддзам π-лы лыд 3,1416. Адриан Меций корсис π = 355/113. Тайӧ лыдӧс позьӧ помнитны кокниа, колӧ сӧмын кыкысьӧн гижны первой куим нечётнӧй лыдпас: 113355 да сы бӧрын бӧръя куим лыдпассӧ янсӧдны воддза куимсьыс.

Шӧр нэмъясӧ нин π лыдӧс вӧлі арталӧма ёна стӧча. Сідз, французскӧй математик Виета (1540—1603) арталіс π дасӧд десятичнӧй знакӧдз стӧчлунӧн. Германскӧй математик Лудольф (1649—1711) арталіс π 35 десятичнӧй знакӧдз стӧча. Та бӧрын π лыд кутісны шуны лудольф лыдӧн. Но сёрджык лои нӧшта стӧчджыка арталӧма π значенньӧ. Сідз, английскӧй математик Шанкс (1812—1882) арталіс 707 знак. Колӧ пасйыны, мый тайӧ бӧръя арталӧмъясыс вайӧны этша пӧльза да оз правдайтны арталӧм вылас видзӧм ыджыд уджсӧ: некоді, дерт, оз пӧльзуйтчы Шанкс лыдӧн.

Бӧльӧ коланаӧсь да тӧдчанаӧсь такӧд йитчан теоретическӧй вопросъяс. Нӧшта ёна важӧн ёна мӧвпалісны кытшвизь веськӧдан задача йылысь, мӧд ногӧн кӧ, веськыдвизя вундӧгӧс построитӧм йылысь, кодлӧн кузьтаыс мед вӧлі сетӧм кытшвизь кузя, да нӧшта мӧвпалісны круг квадратура йылысь, мӧд ног кӧ, сэтшӧм квадратӧс вӧчӧм йылысь, кодлӧн площадьыс мед вӧлі сетӧм круг площадь ыджда. Та дырйи, дерт, ӧтисӧ и мӧд построенньӧсӧ колӧ вӧчны сӧмын кык инструмент отсӧгӧн — линейкаӧн да циркульӧн, мӧд ног кӧ шуны, сӧмын веськыд визьяс да кытшвизьяс вӧчалӧмӧн. Кыкнан тайӧ задачаыс топыда йитчӧны мӧда-мӧдыскӧд. Ми кӧ вермам построитны вундӧг, кодлӧн мед кузьтаыс лои кытшвизь кузьта ыджда, то тайӧ вундӧгсӧ веськыднёльпельӧсалы подувтас пыдди босьтӧмӧн, а радиус джынсӧ — сылы судта пыдди босьтӧмӧн, миян лоас веськыднёльпельӧса, коді лоас сетӧм кругкӧд ӧтгырся; а веськыднёльпельӧсасӧ бергӧдны ӧтгырся квадратӧ абу нин сьӧкыд; тайӧс кужис вӧчны Эвклид нин.

Круг квадратура йылысь да кытшвизьӧс веськӧдӧм йылысь задача ёна интересуйтліс уна геометрӧс, тшӧтш и медся тӧдчанаясӧс. Кытшвизь радиусӧс кӧ босьтам мера единица пыдди, то кытшвизьджынлӧн кузьтаыс петкӧдчас π лыдӧн. Та вӧсна уджыс лоӧ сэтшӧми, мый циркуль да линейка отсӧгӧн колӧ вӧчны вундӧгӧс, кодлӧн кузьтаыс мед петкӧдчис π лыдӧн. Татшӧм построенньӧлӧн позянлуныс та вӧсна зависитӧ π лыд характерысь. 1768 воӧ нин германскӧй математик Ламберт петкӧдліс, мый π лоӧ иррациональнӧй лыд. Сӧмын нӧ, уна иррациональнӧй лыдӧс позьӧ построитны циркульӧн да линейкаӧн. Сідз, 1 (кузьта единица) ыджда бока квадратӧс стрӧитӧм бӧрын да сылысь диагональ нуӧдӧм бӧрын, миян артмас вундӧг, кодлӧн кузьтаыс петкӧдчас лыдӧн. Правильнӧй кӧкъямыспельӧсалӧн бокыс, кодӧс впишитӧма кругӧ, кодлӧн радиусыс единица ыджда, петкӧдчӧ лыдӧн, кодӧс тшӧтш жӧ позьӧ построитны циркульӧн да линейкаӧн. Но π лыдыд сложнӧйджык строенньӧа. Сӧмын колян нэмся мӧд джынйӧ французскӧй математик Эрмит (1873) вермис установитны, мый π лыдӧн выразитӧм вундӧг оз позь построитны циркульӧн либӧ линейкаӧн. Сёрӧнджык тайӧ доказательствосӧ лои кокньӧдӧма да усовершенствуйтӧма уна математикъясӧн. Ӧні тшука тӧдмӧдӧма, мый циркульӧн да линейкаӧн оз позь построитны круг квадратура.

Пасъям, мый бӧльӧ сложнӧйджык инструментъясӧн, мӧд ног кӧ, бӧльӧ сложнӧйджык чукля визьясӧн, тайӧ построенньӧсӧ позьӧ вӧчны, но тайӧс вӧлі ёна важӧн нин тӧдӧны.

6. Теорема. Кык кытшвизь относитчӧны кыдз налӧн радиусъясыс либӧ диаметръясыс.

Сетӧма: C₁ да C₂ — кытшвизьяслӧн кузьтаыс,

R₁ да R₂ да D₁ да D₂ — налӧн радиусъясыс да диаметръясыс.

_____________________________________

Колӧ докажитны: C₁/C₂ = R₁/R₂ = D₁/D₂.

Докажитӧм. C₁ = 2πR₁ = πD₁; C₂ = 2πR₂ = πD₂.

Первой равенствосӧ членӧн-членӧн мӧд равенство вылӧ юкӧм бӧрын лоӧ:

C₁/C₂ = 2πR₁/2πR₂ = R₁/R₂; C₁/C₂ = πD₁/πD₂ = D₁/D₂.

5 §. Дугалӧн кузьта.

Задача 1. Определитны n° дугалысь кузьтасӧ; дугалӧн радиус R (281 серп.).

Решитӧм. AB = n° (дуговӧй) дугалы соответствуйтӧ центральнӧй ∠AOB = n° (пельӧсса). Ӧти дуговӧй градуслӧн кузьтаыс равняйтчӧ 2πR/360 = πR/180, но AB дугаын n°, сідзкӧ, сылӧн a кузьтаыс равняйтчӧ: a = πR∙n/180.

n да 360 лыдъяслы колӧ лоны ӧтинимаӧн; тайӧ лоӧ сійӧ, мый n кӧ сетӧма минутъясӧн, 360° колӧ пӧртны минутъясӧ жӧ.

Задача 2. Определитны кытшвизь радиус ыджда дугалы соответствуйтысь центральнӧй пельӧслысь ыдждасӧ.

Решитӧм. a = πRn/180 формулаысь лоӧ: n° = 180°∙a/πR; условие серти a = R; сідзкӧ

n° = 180°∙R/πR = 180°/π ≈ 57°18’.

Центральнӧй пельӧс, кодлӧн дугаыслӧн кузьтаыс радиус ыджда, шусьӧ радианӧн. Радиан 57°18’ гӧгӧр ыджда; точнӧйджыка 57°17’44,8’’ ыджда.

6 §. Круглӧн, секторлӧн, сегментлӧн площадь.

1. Правильнӧй вписаннӧй да описаннӧй унапельӧсаяслӧн налысь бокъяссӧ помтӧм унаысь кыкпӧлалігӧн площадьясныс — переменнӧй величинаяс. Бокъяслысь лыдсӧ помтӧма ыдждӧдігӧн правильнӧй вписаннӧй унапельӧсалӧн площадь содӧ, а описаннӧйлӧн — чинӧ. Тайӧ кыкнан переменнӧй величинаясыс водзысь-водзӧ мӧда-мӧдыс дінӧ матысмӧны ӧти сійӧ жӧ предел дінӧ стремитчӧмӧн. Предел, код дінӧ найӧ стремитчӧны, эм круглӧн площадь.

Та ногӧн, круглӧн площадь эм правильнӧй вписаннӧй да описаннӧй унапельӧсаяслӧн помтӧм унаысь бокъяс лыдсӧ налысь ыдждӧдігӧн площадьяслӧн предел.

Круглысь площадьсӧ кӧ пасъям K пыр, правильнӧй описаннӧй унапельӧсалысь площадьсӧ — S_оп пыр да правильнӧй вписаннӧй унапельӧсалысь — S_вп пыр, то S_вп < K < S_оп.

Унапельӧсалысь бокъяс лыдсӧ кыкпӧлалӧм серти описаннӧй да вписаннӧй унапельӧсаяслӧн площадьяс костын S_оп − S_вп чинӧ да водзысь-водзӧ лоӧ ичӧтджык да ичӧтджык. Гӧгӧрвоана, мый тайӧ условийӧяс дырйи K − S_вп да S_оп − K разносьтъяс лоӧны S_оп − S_вп разносьтысь ичӧтджыкӧн.

Та вӧсна круг площадь пыдди босьтӧны зэв уна бока правильнӧй вписаннӧй либӧ описаннӧй унапельӧсалысь площадь.

Правильнӧй описаннӧй унапельӧсалӧн площадь S_оп = ½P_опR. Помтӧм унаысь бокъяс лыд кыкпӧлалігӧн унапельӧсалӧн P_оп периметр стремитчӧ пределыс дінӧ — кытшвизь C кузьта дінӧ; такӧд ӧттшӧтш сылӧн S_оп площадь стремитчӧ ас пределыс дінас — круг K площадь дінӧ.

S_оп = ½P_опR равенство лоӧ справедливӧйӧн любӧй бок лыда унапельӧсалы; справедливӧй лоӧ и сэк, кор n зэв ыджыд; но сэки C серти P_оп да K серти S_оп рӧзнитчӧны сэтшӧм ичӧт величинаӧн, мый сійӧс позьӧ шыбитны; та вӧсна равенство справедливӧй и сэк, кор P_оп вежам C пределнас да S_оп вежам K пределнас. Тадз,

K = ½C∙R, (1)

либӧ, круглӧн площадь равняйтчӧ кругкытш джын да радиус кост произведенньӧлы.

(1) формулаӧ C пыдди 2πR пуктӧм бӧрын лоӧ:

K = ½CR = ½∙2πR∙R = πR².

Бӧръя равенствоын кӧ R-сӧ вежны D/2-ӧн, артмас формула:

K = πR² = π(D/2)² = πD²/4 = ¼πD².

Тадз,

K = πR², либӧ K = ¼πD².

1. Круглӧн площадь равняйтчӧ радиусыс квадратлы π лыд вылӧ ӧктӧмӧн.

2. Круглӧн площадь равняйтчӧ диаметрыс квадрат нёльӧд юкӧныслы π лыд вылӧ ӧктӧмӧн.

Следствийӧ. Кык круглӧн площадьяс относитчӧны кыдз радиусъясыслӧн квадратъяс либӧ диаметръясыслӧн квадратъяс.

K₁ да K₂ — кык круглӧн площадьяс; R₁ да R₂ — налӧн радиусъясыс; D₁ да D₂ — налӧн диаметръясыс, сідзкӧ:

K₁ = πR₁² = ¼πD₁²; K₂ = πR₂² = ¼πD₂².

Тайӧ равенствоясӧс членӧн-членӧн юкам да лоӧ:

K₁/K₂ = πR₁²/πR₂² = R₁²/R₂² = D₁²/D₂².

2. Теорема. Секторлӧн площадь равняйтчӧ дуга кузьтаыс да радиусыс произведенньӧ джынлы.

Сетӧма: R радиуса круг (282 серпас);

AB дугалӧн кузьта: = a, AOB секторын n°.

_____________________________

Колӧ докажитны: S_сект = ½aR.

Докажитӧм. R радиуса круглӧн K площадь = πR²; 1° ыджда дугаа секторлӧн площадь круг площадьысь 1/360 ыджда, сідзкӧ, πR²/360 ыджда. n° ыджда AB дугаа AOB секторлӧн площадь лоӧ: S_сект = πR²n/360 = ½∙πRnR/180, но ‿AB = a = πRn/180, та вӧсна

S_сект = ½aR.

3. Сегментлӧн площадь. AMB сегментӧс (283 серп.) граничитӧны AMB = a дуга да AB хорда, — сылӧн площадь артассьӧ кыдз сійӧ жӧ a дугаа AOB секторлӧн площадь костын да AB хордаӧн да кык радиусӧн артмӧм кык ӧткузя бока AOB куимпельӧсалӧн площадь костын разносьт.

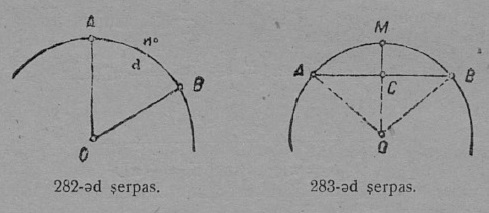
AMB сегментлӧн площадь равняйтчӧ AOB сектор площадьлы AOB куимпельӧса площадьтӧг; секторлӧн площадь = ½aR да куимпельӧсалӧн площадь = ½a_nh_n, та вӧсна сегментлӧн площадь = ½aR − ½a_nh_n.

AMB сегментын (283 серп.) AB хорда шусьӧ сегмент подувтасӧн, сегмент подувтас шӧр пыр мунысь CM = h перпендикуляр шусьӧ сегмент судтаӧн либӧ стрелкаӧн.

Юасянъяс да упражненньӧяс.

1. Унаӧн-ӧ ыдждас кытшвизьлӧн кузьта, кор радиуссӧ ыдждӧдам 1 метрӧн?

2. Кымын пӧв правильнӧй куимпельӧсаӧ вписаннӧй кытшвизь кузьтаыс ичӧтджык описаннӧй кытшвизь кузьтаысь?

3. Кымын пӧв правильнӧй куимпельӧса гӧгӧр описаннӧй круглӧн площадьыс ыджыдджык сійӧ жӧ куимпельӧсаӧ вписаннӧй круг площадьысь?

4. Артавны, унаӧн-ӧ 120° дуга, кодлӧн радиус R = 1 м, ыджыдджык сійӧс стягивайтан хордаысь.

5. Кытшвизь джынлӧн кузьтаыс, кодӧс арталӧма 0,01-ӧдз точносьтӧн матыстӧмӧн a₃ + a₄ ыджда. Прӧверитны.

6. R = 3 м ыджда радиуса куим кытшвизь касайтчӧны ортсысянь. Определитны кытшвизьяс костса “нюкылявизя” куимпельӧсалысь площадь.

7. Веськыдпельӧса куимпельӧсалӧн бокъяс 2a, 2b да 2c. Тайӧ бокъяс вылӧ кыдз диаметръяс вылӧ вӧчӧма кытшвизьяс. Гипотенуза вылӧ вӧчӧм круглӧн площадь равняйтчӧ катетъяс вылӧ вӧчӧм кругъяслӧн площадьяс суммалы. Докажитны.

8. R = 1 м радиуса кытшвизьяс касайтчӧны ортсысянь. Нуӧдны коймӧд кытшвизь сідз, медым сійӧ сетӧм кытшвизьясӧс юкис шӧри, да артавны куимнан кругса ӧтувъя пайыслысь площадьсӧ.

9. R = 2 м радиуса кругӧс концентрическӧй кытшвизьӧн юкӧма шӧри. Определитны концентрическӧй кытшвизьлысь радиуссӧ.

10. Докажитны, мый кытшлӧн^колӧ: кык концентрическӧй кытшӧн артмӧдӧм кольчалӧн/^ площадь π(R + r)(R − r) ыджда, кӧн R да r — ортсыс да пытшкӧс радиусъяс.

_______________________________________

ӦТВЕТЪЯС

II юкӧд 25 лист бок

4. 80° да 100°. 5. 76,5°; 45°. 6. 61°. 8. 90°.

III юкӧд 33 лист бок

3. 5 см, 5 см да 4 см либӧ 4⅓ см, 4⅓ да 5⅓ см.

VI юкӧд 47 лист бок

1. a/2. 2. a да b.

VII юкӧд 58 лист бок

1. AB ∥ CD. 2. CD ⊥ KL. 3. 45° да 135°; 78°45’ да 101°15’; 80° да 100°; 108,5° да 71,5°. 7. 108° да 72°; 80° да 100°; 110° да 70°; 50° да 130°; 108°, 80°, 110° да 50°. 8. 30°, 60° да 90°; оз.

VIII юкӧд 76 лист бок

2. 24,2 см. 11. 10 см.

IX юкӧд 89 лист бок

2. 9 пӧв. 3. Да. 4. 250 м. 5. Квадратлӧн площадьыс 900 см² вылӧ ыджыдджык. 6. Квадратлӧн периметрыс 60 см вылӧ ичӧтджык. 8. 25 см².

XI юкӧд 100 лист бок

6. Кымын колӧ.^A чутыс кӧ абу фиксируйтӧма. — А. В./^ 8. 6 см. 12. 2) 2r вылӧ. 3) 3 см да 7 см радиусъяса концентрическӧй кытшвизьяс. 13. Веськыд визь, коді параллельнӧй сетӧмъяслы да коді мунӧ на шӧракостті, AB да CD костса пельӧсъяслӧн кык биссектриса. 16. Концентрическӧй кытшвизь, кодлӧн радиусыс равняйтчӧ шӧрчутсянь хордаӧдз ылнакостлы.

XII юкӧд 107 лист бок

1. 30°, 35° да 115°. 2. 37,5°, 60° да 82,5°. 5. 80°. 6. 70°.

XIII юкӧд 113 лист бок

2. 8 см да 4 см радиусъяса концентрическӧй кытшвизьяс. 3. 1,5 см; 3 см.

XIV юкӧд 116 лист бок

5. Кытшвизьяс, кодъясӧс вӧчӧма кыдзи диаметр вылӧ, вундӧг вылӧ, кодлӧн помъясыс: сетӧм чут да сетӧм кытшвизьлӧн шӧрчут.

XV юкӧд 128 лист бок

2. Нуӧдны биссектриса. 3. 2; 2; 0,5. 6. 12,8 см да 8 см.

XVI юкӧд 141 лист бок

9. Мӧд да коймӧд. 10. 6 см. 11. 1,5 см да 4,5 см. 12. Веськыднёльпельӧсаяс подобнӧйӧсь сӧмын сэк, кор найӧ квадратъяс.

XVII юкӧд 149 лист бок

1. a) оз, b) да. 2. Ёсьпельӧса; оз вермы лоны. 3. 10 см, 13⅓ см, да 16⅔ см. 4. 4 кг.

XVIII юкӧд 154 лист бок

2. см да см. 3. 4 см. 4. ӧти коймӧд юкӧн.

XIX юкӧд 158–159 лист бок

1. Сы вӧсна, мый 2 + 4 ≠ 3 + 5. 2. Сы вӧсна, мый 1 + 3 ≠ 2 + 4.

9. 7 см.

XX юкӧд 169 лист бок

XXI юкӧд 181 лист бок

4. ≈ 36 см вылӧ. 6. 1,44 м². 8. 2R²(π − 1) ≈ 4,3 м².

ТЕРМИН ӦКТӦД.

Телӧ — тело.

Свойство — свойство.

Форма — форма.

Ыджда — размер.

Сяр — шар.

Пространство — пространство.

Пространство юкӧн — часть простанства.

Кузьта — длина.

Пасьта — ширина.

Судта — высота.

Кызта — толщина.

Веркӧс — поверхность.

Граница — граница.

Визь — линия.

Веськыд визь — прямая линия.

Нюкыля визь — кривая линия.

Горизонтальнӧй веськыд визь — горизонтальная прямая линия.

Вертикальнӧй веськыд визь — вертикальная прямая линия.

Луч — луч.

Вундӧг — отрезок.

Чегласьӧм визь — ломаная линия.

Смешаннӧй визь — смешанная линия.

Плоскӧй веркӧс — плоская поверхность.

Нюкыля веркӧс — кривая поверхность.

Фигура — фигура.

Геометрическӧй образ — геометрический образ.

Аксиома — аксиома.

Теорема — теорема.

Кытшвизь — окружность.

Круг — круг.

Шӧрчут — центр.

Тупкӧса — замкнутый.

Радиус — радиус.

Хорда — хорда.

Диаметр — диаметр.

Дуга — дуга.

Дуга градус — дуговой градус.

Пельӧс градус — угловой градус.

Минут — минута.

Секунд — секунда.

Ӧтыджда, равняйтчӧ — равно.

Пельӧс — угол.

Павтыртӧм пельӧс — развёрнутый угол.

Веськыд пельӧс — прямой угол.

Ёсь пельӧс — острый угол.

Тшӧтшыд пельӧс — тупой угол.

Шӧрса пельӧс — центральный угол.

Йӧртӧм пельӧс — заключённый угол.

Бердса пельӧс — прилежащий угол.

Орчча пельӧс — смежный угол.

Пополнительнӧй пельӧс — пополнительный угол.

Дополнительнӧй пельӧс — дополнительный угол.

Пытшкӧс пельӧс — внутренний угол.

Ортсыс пельӧс — внешний угол.

Паныда пельӧс — противоположный угол.

Бок — сторона.

Подувтас — основание.

Йыв — вершина.

Биссектриса — биссектриса.

Медиана — медиана.

Перпендикуляр — перпендикуляр.

Пӧлыня визь — наклонная линия.

Чут — точка.

Проекция — проекция.

Куимпельӧса — треугольник.

Веськыдпельӧса куимпельӧса — прямоугольный треугольник.

Ёсьпельӧса куимпельӧса — остроугольный треугольник.

Тшӧтшыдпельӧса куимпельӧса — тупоугольный треугольник.

Разнӧй бокъяса куимпельӧса — разносторонний треугольник.

Кык ӧткузя бока куимпельӧса — равнобедренный треугольник.

Ӧткузя бокъяса куимпельӧса — равносторонний треугольник.

Катет — катет.

Гипотенуза — гипотенуза.

Осевӧй симметрия — осевая симметрия.

Симметрия ось — ось симметрии.

Параллельнӧй веськыд визьяс — параллельные прямые линии.

Пытшкӧс ӧтарбокса пельӧс — внутренний односторонний угол.

Ортсыс ӧтарбокса пельӧс — внешний односторонний угол.

Соответственнӧй пельӧс — соответственный угол.

Крестӧнкуйлысь пельӧс — накрест лежащий угол.

Нёльпельӧса — четырёхугольник.

Трапеция — трапеция.

Параллелограмм — параллелограмм.

Квадрат — квадрат.

Ромб — ромб.

Диагональ — диагональ.

Центральнӧй симметрия — центральная симметрия.

Веськыднёльпельӧса — прямоугольник.

Шӧр визь — средняя линия.

Унапельӧса — многоугольник.

Площадь — площадь.

Ӧтинима — одноимённый.

Ӧтгырся — равновеликий.

Ӧтыдждаысь вӧчӧма — равносоставленный.

Геометрическӧй места — геометрическое место.

Ӧтылнаын — равноудалённый.

Касательнӧй визь — касательная линия.

Касанньӧ чут — точка касания.

Шӧрчуткорсьысь — центроискатель.

Вписаннӧй пельӧс — вписанный угол.

Описаннӧй пельӧс — описанный угол.

Отсасьысь — вспомогательный.

Концентрическӧй кытшвизь — концентрическая окружность.

Эксцентрическӧй кытшвизь — эксцентрическая окружность.

Пропорциональнӧй вундӧгъяс — пропорциональные отрезки.

Подобийӧ — подобие.

Поперечнӧй масштаб — поперечный масштаб.

Подобнӧя пукталӧм — подобно расположенные.

Арталӧм — вычисление.

Апофема — апофема.

Сектор — сектор.

Сегмент — сегмент.